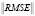Необходимость решения задач оценивания и фильтрации возникает во многих технических приложениях. При этом на практике (например, в задачах радиолокации, связи, навигации и управления) часто встречаются ситуации, связанные с наличием аномальных наблюдений, не содержащих достоверной информации об исследуемой системе. Причина этого может быть связана, например, с неисправностями, приводящими к изменению статистических характеристик данных, а также с отклонением распределения шумов системы и измерений от гауссовского. Использование алгоритмов оценивания, не учитывающих возможность появления аномальных наблюдений, может привести к смещению оценок параметров. В связи с этим представляется целесообразным иметь дело с робастными процедурами оценивания.
Традиционно для решения задач оценивания и фильтрации привлекают фильтр Калмана [1–3], позволяющий находить несмещенные оценки состояния с минимальной дисперсией. Этот фильтр предполагает наличие гауссовских шумов в моделях состояния и наблюдения и будет расходиться при нарушении данного предположения. В настоящий момент разработаны многочисленные робастные модификации фильтра Калмана. Исследований по данной тематике становится все больше [4–6]. В связи с этим возникает практическая целесообразность в сравнении эффективности наиболее популярных робастных фильтров. В этом отношении особое внимание следует уделить появившимся относительно недавно так называемым коррентропийным фильтрам [7–9]. Эти фильтры являются наиболее популярными и заключаются в использовании в качестве критерия оптимальности критерия максимума коррентропии. Коррентропия определяется как статистическая мера близости между двумя случайными величинами и позволяет учитывать моменты второго и более высокого порядка. Таким образом, применение данных фильтров способствует получению качественных оценок вектора состояния при наличии негауссовских шумов.
В [10] был проведен сравнительный анализ некоторых широко известных робастных фильтров для нестационарных линейных дискретных систем. В результате проведенных исследований выявлены два наиболее эффективных фильтра. Ими оказались фильтры Изанлу (Izanloo) – Фейкуриана (Fakoorian) – Джазди (Yazdi) – Саймона (Simon) [7] и Сярккя (Sarkka) – Нумменмаа (Nummenmaa) [4], известные по англоязычным публикациям как фильтры MCC-KF (От Maximum Correntropy Criterion Kalman Filter) и VB-AKF (От Variational Bayesian Adaptive Kalman Filter) соответственно. Настоящая работа является продолжением и естественным развитием основных результатов из [10].
На примере непрерывно-дискретной модели прямолинейного равноускоренного движения объекта провести сравнительный анализ эффективности указанных фильтров с двумя новыми коррентропийными фильтрами и выявить наиболее качественные из них.
Рассмотрим следующую управляемую, наблюдаемую модель стохастической системы в пространстве состояний:
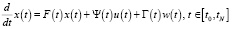, (1)
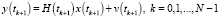. (2)
Здесь x(t) – n – вектор состояния, u(t) – детерминированный r – вектор управления, w(t) – p – вектор шума системы (возмущения), y(tk+1) – m – вектор измерения (наблюдения), v(tk+1) – m – вектор шума измерения.
Будем считать, что:
– случайные векторы w(t) и v(tk+1) являются стационарными белыми гауссовскими шумами, для которых
, 
,
, 
,
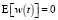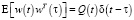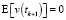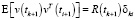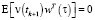
(здесь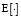 
– оператор математического ожидания, ?(t – ?δ(t – τ) – дельта-функция Дирака, δki – символ Кронекера);
– начальное состояние x(t0) имеет нормальное распределение с параметрами
, 
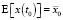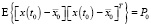
и не коррелирует с w(t) и v(tk+1).
Необходимо для математической модели (1), (2) с учетом указанных априорных предположений при наличии аномальных наблюдений провести исследование эффективности некоторых перспективных, по нашему мнению, робастных фильтров.
Описание исследуемых фильтров
Приведем ниже некоторые современные адаптивные фильтры, позволяющие получать оценки вектора состояния, а также ковариационной матрицы ошибок оценивания при наличии аномальных наблюдений.
Имея дело с негауссовскими шумами в (1), (2), методы максимальной коррентропии предполагают вместо классического критерия минимума среднеквадратичной ошибки использовать следующий критерий оптимальности:
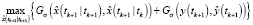, (3)
где
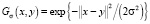– функция ядра Гаусса;
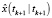– оценка фильтрации вектора состояния в момент времени tk+1;
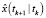– оценка одношагового предсказания вектора состояния;
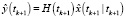– оценка y(tk+1), полученная по измерениям y(t1),…, y(tk+1).
Следует уточнить, что выбор размера ядра σ существенно влияет на качество работы коррентропийных фильтров. К сожалению, в настоящий момент еще не предложена какая-либо методика для априорного определения σ. В связи с этим данный параметр приходится подбирать опытным путем, что пока является слабым местом всех коррентропийных фильтров. Дополнительно уточним, что при больших значениях σ коррентропийные фильтры начинают работать значительно хуже, так как все более начинают походить на классический фильтр Калмана.
Фильтр Изанлу – Фейкуриана – Джазди – Саймона сочетает в себе критерий максимальной коррентропии и метод взвешенных наименьших квадратов и использует один шаг метода простых итераций для решения возникающего при оптимизации критерия (3) нелинейного уравнения. Приведем алгоритм данного фильтра с использованием эквивалентных форм представления матричного коэффициента усиления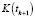 
и ковариационной матрицы ошибок фильтрации 
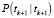из [11].
Инициализация:
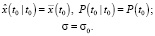
Выполнять в цикле по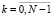 
Одношаговое предсказание:
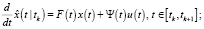
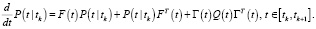
Фильтрация:
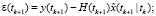
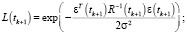
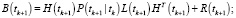
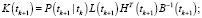
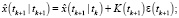
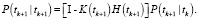
Конец цикла.
В фильтре Чена – Лю – Чжао – Принципэ (в англоязычных публикациях он известен как фильтр MCKF (От Maximum Correntropy Kalman filter)) [8] для решения оптимизационной задачи (3) был предложен новый алгоритм, использующий несколько шагов метода простых итераций (их количество зависит от выбранного параметра ε), обладающий высокой сходимостью и позволяющий находить оценки фильтрации и ковариационной матрицы ошибки фильтрации.
Инициализация:
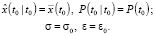
Выполнять в цикле по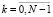 
Одношаговое предсказание:
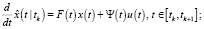
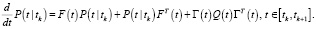
Фильтрация:
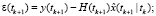
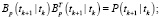
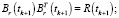
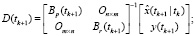
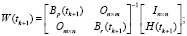
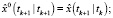
Выполнять в цикле по 
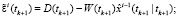
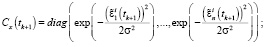
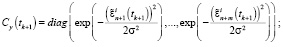
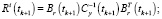
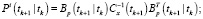
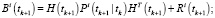
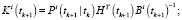
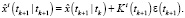
Если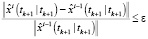 
, то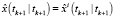 
и конец цикла по i.
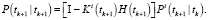
Конец цикла по k.
Фильтр Вана – Гао – Чжана – Ма (в англоязычных публикациях он известен как фильтр VBMCGF (От Variation Beysian Maximum Correntropy Gaussian Filter)) [9] так же основан на критерии максимальной коррентропии в сочетании с вариационным байесовским оцениванием и используется при оценивании вектора состояния системы с неизвестными ковариационными матрицами негауссовских шумов.
Инициализация:
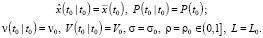
Выполнять в цикле по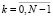 
Одношаговое предсказание:
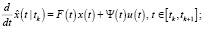
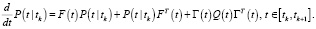
Фильтрация:
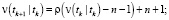
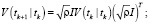
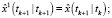
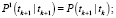
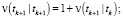
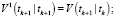
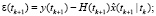
Выполнять в цикле по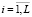 
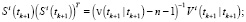
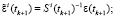
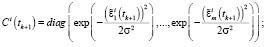
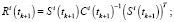
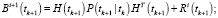
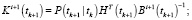
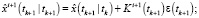
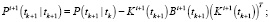
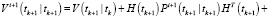
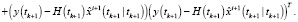
Конец цикла по i.
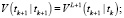
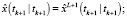
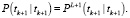
Конец цикла по k.
Фильтр Сярккя – Нумменмаа не относится к коррентропийным. Он получен на основе вариационного байесовского оценивания в предположении, что ковариационная матрица шума измерений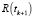 
порядка m считается диагональной и неизвестной.
Инициализация:
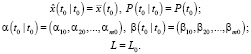
Выполнять в цикле по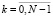 
Одношаговое предсказание:
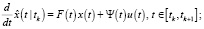
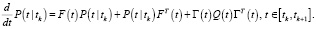
Фильтрация:
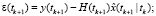
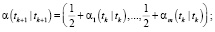
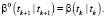
Выполнять в цикле по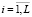 
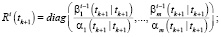
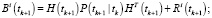
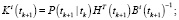
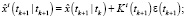
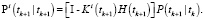
Выполнять в цикле по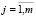 
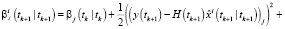
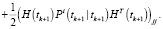
Конец цикла по j.
Конец цикла по i.
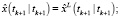
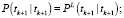
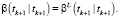
Конец цикла по k.
Результаты исследования и их обсуждение
Проведем исследование эффективности указанных подходов на примере модели прямолинейного равноускоренного движения объекта под влиянием внешней среды. Первая компонента состояния – это положение объекта, вторая – скорость, третья – ускорение. Предположим, измеряется (с некоторой ошибкой) скорость объекта. Модели состояния и измерения приведены ниже.
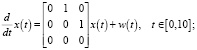
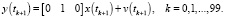
Будем считать, что выполняются все априорные предположения, высказанные при постановке задачи, причем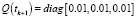 
, 
, 
, 
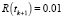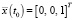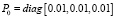. Примем, что измерения производятся равномерно через каждые 
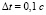и значения различных параметров в исследуемых фильтрах выбраны в соответствии с табл. 1.
Таблица 1
Значение параметров робастных фильтров
|
Фильтр |
Значение параметров фильтра |
|
MCC-KF |
σ0 = 10 |
|
MCKF |
σ0 = 10, ε0 = 10-8 |
|
VBMCGF |
v0 = 4, V0 = diag[0,1, 0,1], σ0 = 10, ρ0 = 0,8, L0 = 4 |
|
VB-AKF |
αi0 = βi0 = 1, i = 1,...,m, L0 = 4 |
Смоделируем с помощью программной среды Matlab выборку с аномальными наблюдениями, задав коэффициент загрязнения выборки λ = 0,1 и дисперсию шума аномальных наблюдений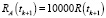 
. Предположим, что обрабатываются данные со случайным характером аномальных измерений. Приведем графическое представление результатов фильтрации на рисунке.
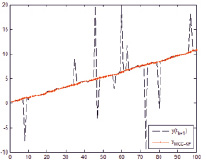
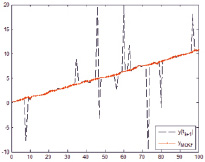
а) б)
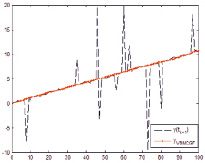
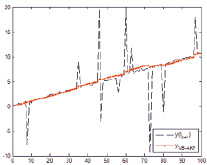
в) г)
Графическое представление y(tk+1) и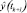 
при использовании: а) MCC-KF; б) MCKF; в) VBMCGF; г) VB-AKF
Для ослабления зависимости результатов оценивания от выборочных данных проведем M = 100 различных запусков системы. О качестве оценивания будем судить по значению усредненного квадратного корня среднеквадратичной ошибки (Root Mean Square Error), которое будем вычислять для каждой компоненты вектора состояния по следующей формуле:
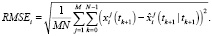
Здесь под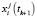 
и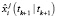 
понимаются, соответственно, значения i-й компоненты вектора состояния и оценки фильтрации, полученные при j-м запуске системы. Численные результаты фильтрации представлены в табл. 2.
Таблица 2
Численные результаты процедуры фильтрации
|
Фильтр |
RMSE1 |
RMSE2 |
RMSE3 |
|
|
MCC-KF |
0,180 |
0,093 |
0,112 |
0,232 |
|
MCKF |
0,173 |
0,092 |
0,107 |
0,224 |
|
VBMCGF |
0,271 |
0,162 |
0,111 |
0,334 |
|
VB-AKF |
0,926 |
0,358 |
0,133 |
1,002 |
Исходя из табл. 2, можно сделать вывод, что среди рассмотренных фильтров наиболее устойчивыми к обработке измерительных данных с аномальными наблюдениями оказались фильтры Изанлу – Фейкуриана – Джазди – Саймона и Чена – Лю – Чжао – Принципэ.
Выводы
В работе проведено исследование эффективности некоторых современных робастных фильтров для моделей стохастических непрерывно-дискретных систем. При этом наилучшие и вполне сопоставимые между собой результаты показали фильтры Изанлу – Фейкуриана – Джазди – Саймона и Чена – Лю – Чжао – Принципэ. Учитывая относительную простоту программной реализации первого из указанных фильтров, авторы рекомендуют его к практическому применению.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-31-00283.