Теория краевых задач для вырождающихся гиперболического и смешанного типов уравнений в настоящее время является одними из важных разделов теории дифференциальных уравнений с частными производными. Это обусловлено как непосредственными связями уравнений смешанного типа с проблемами теории сингулярных интегральных уравнений, теорией интегральных преобразований и специальных функций, так и прикладными задачами механики и математической физики, сводящимися к таким уравнениям. Основы этой теории были заложены в трудах Ф. Трикоми и С. Геллерстедта. Возникшие в приложениях проблемы околозвукового течения сжимаемой среды в плоской постановке и безмоментной теории оболочек описываются уравнениями смешанного типа, для которых как задача Трикоми, так и ее математические обобщения имеют вполне определенный физический смысл.
За последние годы исследования задач со смещением для вырождающихся гиперболических и смешанного типов уравнений ведутся особенно интенсивно. Актуальность этих исследований можно обосновать как внутренними потребностями теоретического обобщения классических задач для уравнений математической физики, так и прикладным значением поскольку они связаны с задачами газовой динамики, теории теплопроводности, теории упругости, теории оболочек, теории плазмы, математической биологии и многими другими вопросами механики. Нелокальные задачи встречаются при математическом моделировании нефтяных пластов, фильтрации грунтовых вод, переноса тепла и массы в объекте, имеющем сложное строение, электрических колебаний в проводах, движения жидкости в канале, окруженном пористой средой, и других явлениях. Для уравнений смешанного типа нелокальные задачи исследовались в работах [1–6, 9]. Данная статья является продолжением этих исследований.
Постановка задачи
Рассмотрим уравнение смешанного типа
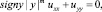(1)
где m = const > 0, в конечной области Ω ограниченной жордановой кривой σ с концами в точках A(0, 0), B(1, 0), расположенной в полуплоскости y > 0 и характеристиками уравнения (1)
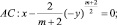
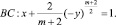
Пусть Ω1 и Ω2 – эллиптическая и гиперболическая части смешанной области Ω. Под регулярным решением уравнения (1) будет пониматься функция u(x, y) из класса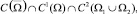 
удовлетворяющая уравнению (1) в 
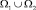и такая, что uy(x, 0), ux(x, 0) могут обращаться в бесконечность порядка ниже единицы на концах A и B интервала J: 0 < x< 1 прямой y = 0.
Задача.
Найти регулярное в области Ω решение u(x, y) уравнения (1), удовлетворяющее условиям
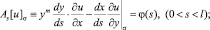(2)
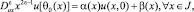(3)
где s – длина кривой σ, отсчитываемая от точки B; θ0(x) – точка пересечения характеристики уравнения (1), входящей из точки (x, 0) ∈ J с характеристикой AC; φ(s), α(x), β(x) – заданные функции, причем φ(s) ∈ C1(σ),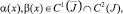 
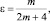
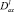– операторы дробного в смысле Римана – Лиувилля интегро-дифференцирования [7, 10].
Доказательство единственности решения задачи
Теорема. В области Ω не может существовать более одного регулярного решения задачи, если выполнены условия
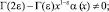(4)
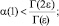
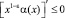. (5)
Доказательство. Примем следующие обозначения
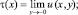
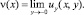
Решение задачи Коши для уравнения (1) в области Ω2 имеет вид [1]
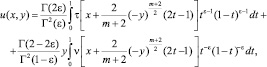(6)
где Г(α) – гамма функция Эйлера.
Удовлетворив (6) условию (3), получим
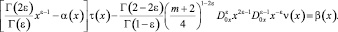
Или, пользуясь известным соотношением [9]
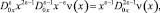
будем иметь соотношение между τ(x) и ν(x), принесенное на J из гиперболической части Ω2 смешанной области Ω
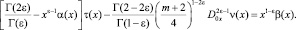(7)
Теорему единственности можно доказать, предварительно доказав, что если u(x, y) является решением уравнения (1), удовлетворяющим однородным условиям (2), (3), то интеграл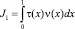 
не может быть отрицательным. В этом случае единственность решения задачи будет следовать из соотношений
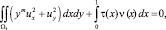J1 ≥ 0. (8)
Покажем, что при выполнении условий (4), (5), интеграл J1 ≥ 0. Полагая β(x) = 0, перепишем (7) в виде
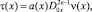
где
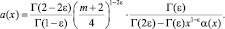
Рассмотрим интеграл
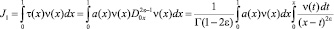
или
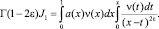
Воспользуемся известной формулой для гамма-функции [7]
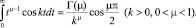
Полагая в ней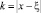 
, μ = 2ε, получим
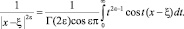
Откуда находим
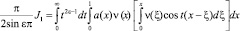
или, что то же самое,
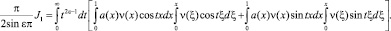
С учетом того, что
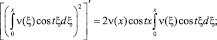
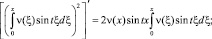
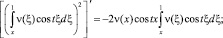
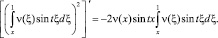
Получим
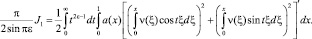
Проинтегрировав последнее выражение по частям, найдем
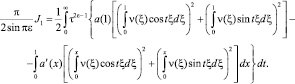
При выполнении условий (5) будет выполняться a(1) > 0, a′(x) ≤ 0.
Действительно,
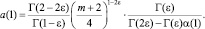
Так как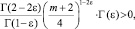 
то при Г(2ε) – Г(ε)α(1) > 0 будет выполнено a(1) > 0, что обеспечивается первым из условий (5).
Далее a′(x) ≤ 0 будет выполнено, если
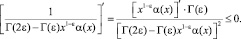
Таким образом, a′(x) ≤ 0 следует из второго из условий (5). Следовательно, J1 ≥ 0.
Из условия (8) – сумма двух неотрицательных слагаемых равна нулю и можно заключить, что
.
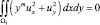Отсюда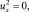 
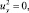следовательно, u(x, y) ≡ c в Ω1, где c = const. Таким образом, в эллиптической части Ω1 u(x, y) = c. Следовательно, u(x, 0) = τ(x) = c, uy(x, 0) = ν(x) = 0.
Соотношение между τ(x) и ν(x) из гиперболической части Ω2 при β(x) = 0 имеет вид
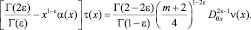
Подставляя τ(x) = c и ν(x) = 0, получим
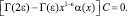
Но так как, согласно условию (4)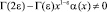 
, то должно выполняться c = 0.
Отсюда заключаем, что u(x, y) ≡ 0 в Ω1, а в Ω2 u(x, y) ≡ 0 как решение задачи Коши с нулевыми данными: τ(x) = 0 и ν(x) = 0. Таким образом, u(x, y) ≡ 0 в Ω и решение задачи единственно.
Доказательство существования решения задачи. Переходя к доказательству существования решения задачи относительно кривой σ будем предполагать, что:
1) x = x(s), y = y(s) – параметрические уравнения кривой σ, где s – длина дуги, отсчитываемая от точки B, функции x′(s), y′(s) I C[0, l], причем x′(s), y′(s) одновременно в нуль не обращаются, производные x″(s), y″(s) удовлетворяют условию Гельдера на [0, l], где l – длина σ;
2) в окрестности концов σ выполнено условие
,
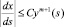где C – постоянная.
Соотношения между τ(x) и ν(x), принесенные на J из эллиптической и гиперболической частей смешанной области Ω, имеют соответственно вид (7) и
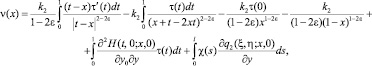(9)
где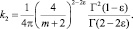 
Свойства функций H(ξ, η; x, y), q2(ξ, η; x, y) подробно приведены в [1].
Исключая ν(x) из (7) и (9), получим
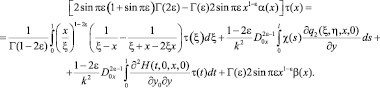(10)
Уравнение (10) с учетом тождества
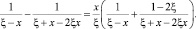
и обозначения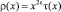 
примет вид
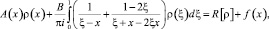(11)
где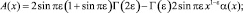 
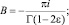
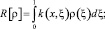
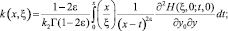
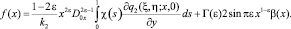
В результате замены
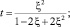
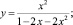
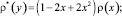
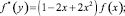
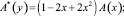
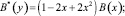
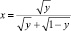
получим сингулярное интегральное уравнение [8]
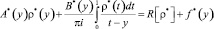(12)
Пусть
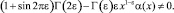
В силу того, что
,
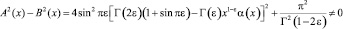уравнение (12) есть сингулярное интегральное уравнение нормального типа, решение которого может быть построено согласно общей теории [8].
Оператор R[ρ*] является вполне непрерывным [8], а из свойств функции Грина и функции k(x, ξ) следует, что
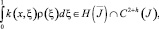
где h > 0,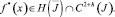 
Отсюда заключаем, что искомая функция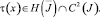 
По найденному τ(x) можно определить ν(x) ∈ C1(J) из (9), причем τ′(x) и ν(x) могут обращаться в бесконечность порядка ниже единицы на концах A и B интервала J, а затем решение u(x, y) задачи в области Ω1 как решение задачи As[u]σ = φ(s), u(x, 0) = τ(x), а в области Ω2 как решение задачи Коши u(x, 0) = τ(x), uy(x, 0) = ν(x).