Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Кумыкова С.К. 1 Эржибова Ф.А. 1 Гучаева З.Х. 1

---

1 Кабардино-Балкарский государственный университет им. Х.М. Бербекова

Работа посвящена исследованию вопроса однозначной разрешимости нелокальной задачи для уравнения смешанного эллиптико-гиперболического типа, когда на эллиптической части границы области задана конормальная производная от искомого решения, а на характеристической части границы области задано нелокальное условие, поточечно связывающее дробную производную от значения решения на характеристике со значением решения на линии вырождения. При определенных ограничениях неравенственного типа на известные функции методом интегралов энергии доказана теорема единственности. Вопрос существования решения задачи методом регуляризации Карлемана – Векуа с помощью подстановки Мануэлла эквивалентно редуцирован к вопросу разрешимости сингулярного интегрального уравнения с ядром Коши второго рода. Выписано условие, гарантирующее существование регуляризатора, приводящего сингулярное интегральное уравнение к уравнению Фредгольма второго рода, безусловная разрешимость которого следует из единственности решения задачи. Определив след решения на линии вырождения и производную от него, решение рассматриваемой задачи определяется как решение задачи Холмгрена в эллиптической части рассматриваемой области и задачи Коши в гиперболической части.

Статья в формате PDF

0 KB

оператор дробного дифференцирования

уравнение смешанного типа

уравнение Фредгольма

сингулярное интегральное уравнение

1. Бицадзе А.В. Некоторые классы уравнений в частных производных. – М.: Наука, 1981. – 448 с.

2. Бицадзе А.В., Самарский А.А. О некоторых простейших обобщениях линейных эллиптических краевых задач // Докл. АН СССР. – 1969. – Т. 185. – № 4. – С. 739–740.

3. Водахова В.А., Гучаева З.Х. Задача Дирихле для смешанного параболо – гиперболического уравнения с разрывными коэффициентами // Успехи современного естествознания. – 2013. – № 11. – С. 136–140.

4. Езаова А.Г. Об одной нелокальной задаче для уравнения смешанного типа третьего порядка // Известия Кабардино-Балкарского государственного университета. – 2011. – Т. 1. – № 4. – С. 26–31.

5. Кумыкова С.К., Халилова Л.А. Задача с операторами дробного интегро-дифференцирования Римана – Лиувилля в краевом условии для вырождающегося гиперболического уравнения // Успехи современного естествознания. – 2015. – № 1–2. – С. 228–231.

6. Кумыкова С.К., Шарданова М.А. Задача Бицадзе – Самарского для уравнения смешанного типа в неограниченной области // Успехи современного естествознания. – 2015. – № 1–1. – С. 80–83.

7. Лебедев Н.Н. Специальные функции и их приложения. – М.-Л., 1963. – 358 с.

8. Мусхелишвили Н.И. Сингулярные интегральные уравнения. – М.: Наука, 1968. – 512 с.

9. Репин О.А., Кумыкова С.К. Об одном классе нелокальных задач для гиперболического уравнения с вырождением типа и порядка // Вестник Самарского государственного технического университета. Серия: Физико-математические науки. – 2014. – № 4 (37). – С. 22–32.

10. Самко С.Г., Килбас А.А. Маричев О.И. Интегралы и производные дробного порядка и некоторые их приложения. – Минск: Наука и техника, 1987. – 688 с.

Теория краевых задач для вырождающихся гиперболического и смешанного типов уравнений в настоящее время является одними из важных разделов теории дифференциальных уравнений с частными производными. Это обусловлено как непосредственными связями уравнений смешанного типа с проблемами теории сингулярных интегральных уравнений, теорией интегральных преобразований и специальных функций, так и прикладными задачами механики и математической физики, сводящимися к таким уравнениям. Основы этой теории были заложены в трудах Ф. Трикоми и С. Геллерстедта. Возникшие в приложениях проблемы околозвукового течения сжимаемой среды в плоской постановке и безмоментной теории оболочек описываются уравнениями смешанного типа, для которых как задача Трикоми, так и ее математические обобщения имеют вполне определенный физический смысл.

За последние годы исследования задач со смещением для вырождающихся гиперболических и смешанного типов уравнений ведутся особенно интенсивно. Актуальность этих исследований можно обосновать как внутренними потребностями теоретического обобщения классических задач для уравнений математической физики, так и прикладным значением поскольку они связаны с задачами газовой динамики, теории теплопроводности, теории упругости, теории оболочек, теории плазмы, математической биологии и многими другими вопросами механики. Нелокальные задачи встречаются при математическом моделировании нефтяных пластов, фильтрации грунтовых вод, переноса тепла и массы в объекте, имеющем сложное строение, электрических колебаний в проводах, движения жидкости в канале, окруженном пористой средой, и других явлениях. Для уравнений смешанного типа нелокальные задачи исследовались в работах [1–6, 9]. Данная статья является продолжением этих исследований.

Постановка задачи

Рассмотрим уравнение смешанного типа

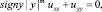(1)

где m = const > 0, в конечной области Ω ограниченной жордановой кривой σ с концами в точках A(0, 0), B(1, 0), расположенной в полуплоскости y > 0 и характеристиками уравнения (1)

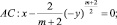
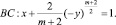
Пусть Ω1 и Ω2 – эллиптическая и гиперболическая части смешанной области Ω. Под регулярным решением уравнения (1) будет пониматься функция u(x, y) из класса 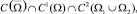удовлетворяющая уравнению (1) в 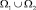и такая, что uy(x, 0), ux(x, 0) могут обращаться в бесконечность порядка ниже единицы на концах A и B интервала J: 0 < x< 1 прямой y = 0.

Задача.

Найти регулярное в области Ω решение u(x, y) уравнения (1), удовлетворяющее условиям

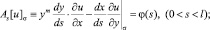(2)

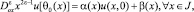(3)

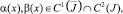
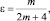
где s – длина кривой σ, отсчитываемая от точки B; θ0(x) – точка пересечения характеристики уравнения (1), входящей из точки (x, 0) ∈ J с характеристикой AC; φ(s), α(x), β(x) – заданные функции, причем φ(s) ∈ C¹(σ), 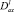– операторы дробного в смысле Римана – Лиувилля интегро-дифференцирования [7, 10].

Доказательство единственности решения задачи

Теорема. В области Ω не может существовать более одного регулярного решения задачи, если выполнены условия

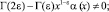(4)

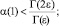
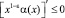. (5)

Доказательство. Примем следующие обозначения

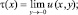
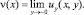
Решение задачи Коши для уравнения (1) в области Ω2 имеет вид [1]

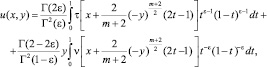(6)

где Г(α) – гамма функция Эйлера.

Удовлетворив (6) условию (3), получим

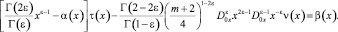
Или, пользуясь известным соотношением [9]

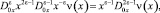
будем иметь соотношение между τ(x) и ν(x), принесенное на J из гиперболической части Ω₂ смешанной области Ω

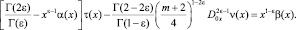(7)

Теорему единственности можно доказать, предварительно доказав, что если u(x, y) является решением уравнения (1), удовлетворяющим однородным условиям (2), (3), то интеграл 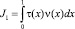не может быть отрицательным. В этом случае единственность решения задачи будет следовать из соотношений

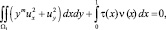J₁ ≥ 0. (8)

Покажем, что при выполнении условий (4), (5), интеграл J₁ ≥ 0. Полагая β(x) = 0, перепишем (7) в виде

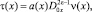
где

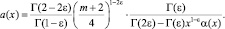
Рассмотрим интеграл

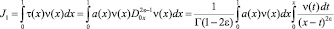
или

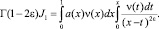
Воспользуемся известной формулой для гамма-функции [7]

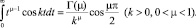
Полагая в ней 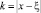, μ = 2ε, получим

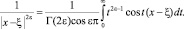
Откуда находим

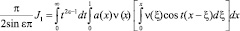
или, что то же самое,

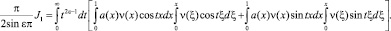
С учетом того, что

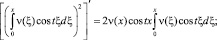
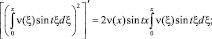
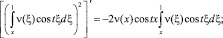
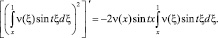
Получим

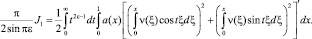
Проинтегрировав последнее выражение по частям, найдем

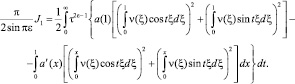
При выполнении условий (5) будет выполняться a(1) > 0, a′(x) ≤ 0.

Действительно,

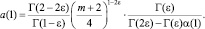
Так как 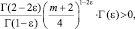то при Г(2ε) – Г(ε)α(1) > 0 будет выполнено a(1) > 0, что обеспечивается первым из условий (5).

Далее a′(x) ≤ 0 будет выполнено, если

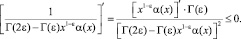
Таким образом, a′(x) ≤ 0 следует из второго из условий (5). Следовательно, J₁ ≥ 0.

Из условия (8) – сумма двух неотрицательных слагаемых равна нулю и можно заключить, что

.

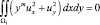Отсюда 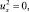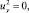следовательно, u(x, y) ≡ c в Ω₁, где c = const. Таким образом, в эллиптической части Ω₁ u(x, y) = c. Следовательно, u(x, 0) = τ(x) = c, uy(x, 0) = ν(x) = 0.

Соотношение между τ(x) и ν(x) из гиперболической части Ω₂ при β(x) = 0 имеет вид

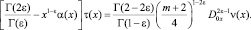
Подставляя τ(x) = c и ν(x) = 0, получим

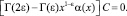
Но так как, согласно условию (4) 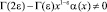, то должно выполняться c = 0.

Отсюда заключаем, что u(x, y) ≡ 0 в Ω1, а в Ω2 u(x, y) ≡ 0 как решение задачи Коши с нулевыми данными: τ(x) = 0 и ν(x) = 0. Таким образом, u(x, y) ≡ 0 в Ω и решение задачи единственно.

Доказательство существования решения задачи. Переходя к доказательству существования решения задачи относительно кривой σ будем предполагать, что:

1) x = x(s), y = y(s) – параметрические уравнения кривой σ, где s – длина дуги, отсчитываемая от точки B, функции x′(s), y′(s) I C[0, l], причем x′(s), y′(s) одновременно в нуль не обращаются, производные x″(s), y″(s) удовлетворяют условию Гельдера на [0, l], где l – длина σ;

2) в окрестности концов σ выполнено условие

,

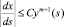где C – постоянная.

Соотношения между τ(x) и ν(x), принесенные на J из эллиптической и гиперболической частей смешанной области Ω, имеют соответственно вид (7) и

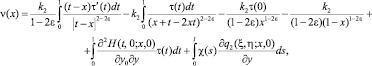(9)

где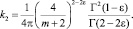

Свойства функций H(ξ, η; x, y), q2(ξ, η; x, y) подробно приведены в [1].

Исключая ν(x) из (7) и (9), получим

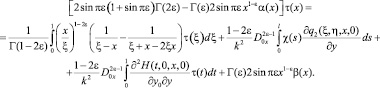(10)

Уравнение (10) с учетом тождества

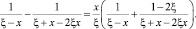
и обозначения 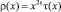примет вид

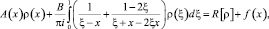(11)

где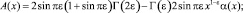

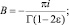
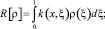
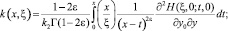
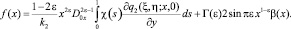
В результате замены

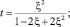
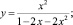
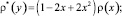
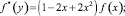
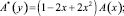
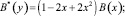
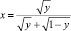
получим сингулярное интегральное уравнение [8]

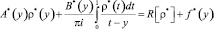(12)

Пусть

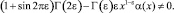
В силу того, что

,

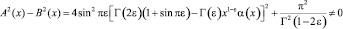уравнение (12) есть сингулярное интегральное уравнение нормального типа, решение которого может быть построено согласно общей теории [8].

Оператор R[ρ*] является вполне непрерывным [8], а из свойств функции Грина и функции k(x, ξ) следует, что

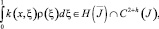
где h > 0,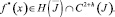

Отсюда заключаем, что искомая функция 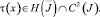По найденному τ(x) можно определить ν(x) ∈ C1(J) из (9), причем τ′(x) и ν(x) могут обращаться в бесконечность порядка ниже единицы на концах A и B интервала J, а затем решение u(x, y) задачи в области Ω1 как решение задачи As[u]_σ = φ(s), u(x, 0) = τ(x), а в области Ω2 как решение задачи Коши u(x, 0) = τ(x), uy(x, 0) = ν(x).

Библиографическая ссылка