Анализ математических моделей по оценке напряженно-деформированного состояния конструкций, армированных дискретными волокнами, показал, что более точно отразить фактическое состояние элементов под нагрузкой позволяет нелинейно-деформационная модель, предложенная В.Н. Байковым, Н.И. Карпенко, Б.С. Расторгуевым, Т.А. Мухамедиевым [2, 3, 4]. Данная модель основывается на условиях равновесия нормального сечения, разбитого на дискретные участки матрицы и армирующие элементы.
Учет физической нелинейности работы конструкций производится с помощью математического описания диаграмм деформирования армирующего волокна, бетона-матрицы и применения шагово-итерационного метода, реализующего способ упругих решений А.А. Ильюшина. Суть метода заключается в том, что решение нелинейной задачи получается в виде последовательности решений линейных задач, сходящихся к результату.
Для случая, когда армирование изгибаемого элемента производится дисперсно-распределенными дискретными волокнами, – фиброй, – условия равновесия внешних и внутренних сил при любом загружении записываются в виде
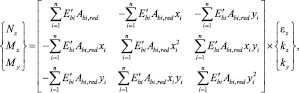(1)
где Nz – продольная сила; Mx – изгибающий момент в направлении оси X; My – изгибающий момент в направлении оси Y; Abi,red – приведенная площадь i-го дискретного элемента матрицы композита; σbi – напряжение в i-м дискретном элементе матрицы; Asj – площадь поперечного сечения j-го непрерывного волокна (арматуры) в матрице композита; σsj – напряжение в сечении j-го волокна матрицы.
Учитывая, что напряжения в дискретных элементах бетона и волокна определяются из диаграмм деформирования материалов, получают
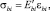(2)
где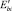 
– секущий модуль деформаций матрицы, зависящий от уровня загружения.
Приведенная площадь сечения Abi,red фибробетонного элемента определяется по формуле
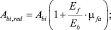
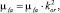(3)
где µfv – коэффициент армирования элемента дискретными волокнами по объему; kor – коэффициент, учитывающий ориентацию волокон в объеме элемента в зависимости от геометрических размеров волокон и дискретных элементов сечения:
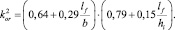(4)
Здесь b – средняя ширина сечения изгибаемого элемента; hi – толщина слоя, армированного дискретными волокнами; lf – длина фибрового волокна.
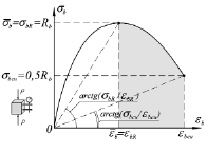
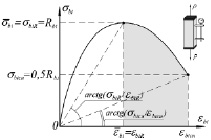
Согласно новым нормам проектирования кусочно-линейные диаграммы деформирования бетона носят достаточно условный характер и приближенно учитывают поведение материала под нагрузкой [1]. Вследствие этого для расчета напряженно-деформированного состояния сжатого (растянутого) бетона были предложены криволинейные диаграммы с ниспадающей ветвью (рис. 1) [5]. Аналитические зависимости для описания криволинейных диаграмм с ниспадающей ветвью принимаются согласно рекомендациям международных норм (CEB-FIP MODEL CODE, 1990):
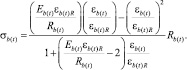(5)
Значение максимальных относительных деформаций бетона ε b(t)cu определяют по формуле
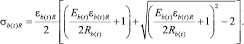(6)
Эти значения деформаций соответствуют напряжениям 0,5Rb(t) в области ниспадающей ветви диаграммы.
а б
Рис. 1. Криволинейные диаграммы состояния сжатого (а) и растянутого (б) бетона с ниспадающей ветвью
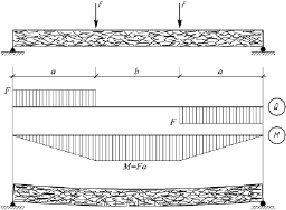
Рис. 2. Схема образования нормальных к продольной оси трещин в зоне чистого изгиба однопролетной фибробетонной балки
При создании алгоритма анализа напряженно-деформированного состояния (НДС) изгибаемого элемента с дискретными волокнами по детерминированной математической модели необходимо учитывать все стадии его разрушения.
Рассмотрим однопролетную фибробетонную балку, свободно лежащую на двух опорах, симметрично загруженную двумя сосредоточенными силами F (рис. 2).
Балка разрушается в зоне чистого изгиба; нормальное (центральное) сечение проходит последовательно через три характерные стадии НДС, отличающиеся между собой как в количественном, так и в качественном отношении.
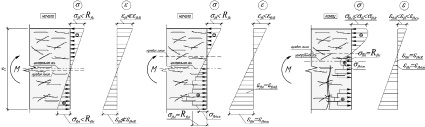
Под первой стадией разрушения здесь понимают НДС элемента до образования трещин в его растянутой зоне, т.е. когда напряжения почти пропорциональны деформациям (рис. 3, а); деформации растянутой зоны не превосходят значения εfbtR (предельные деформации, соответствующие пределу прочности фибробетона на растяжение Rfbt); эпюры нормальных напряжений в композите сжатой и растянутой зон сечения по форме близки к треугольным.
С увеличением нагрузки развиваются неупругие деформации в растянутой зоне элемента; эпюра напряжений в ней становится криволинейной; величина напряжений приближается к временному сопротивлению фибробетона на осевое растяжение. Когда деформации удлинения крайних растянутых волокон достигнут предельной величины εfbtR, наступает конец первой стадии. При этом растягивающее напряжение в бетоне у нижней кромки достигает предела прочности фибробетона при растяжении Rfbt; в сжатой зоне эпюра напряжений близка к треугольной. При дальнейшем увеличении нагрузки в бетоне растянутой зоны образуются трещины, рост которых сдерживается множественными дискретными волокнами.
а б в
Рис. 3. Стадии напряженно-деформированного состояния изгибаемого фибробетонного элемента: а – 1-ая стадия; б – 2-ая стадия; в – 3-я стадия
Под второй стадией понимают НДС элемента, когда в фибробетоне его растянутой зоны интенсивно образуются и раскрываются трещины. В местах трещин растягивающие усилия в основном воспринимает дискретное волокно, – стальная фибра, – и частично бетон над трещиной (рис. 3, б).
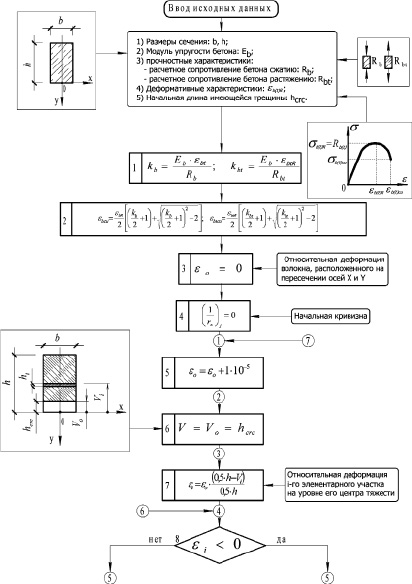
Рис. 4. Алгоритм программы, оценивающей НДС изгибаемых элементов на основе детерминированной математической модели (начало)
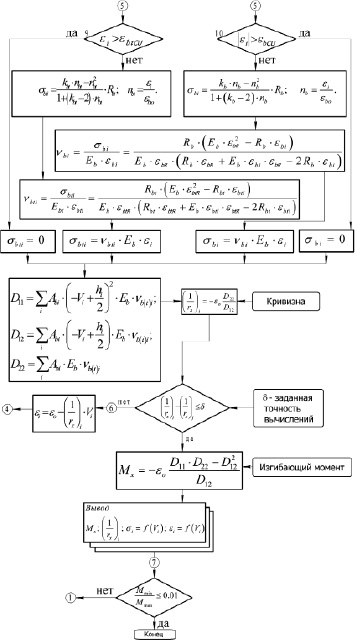
Рис. 5. Алгоритм программы, оценивающей НДС изгибаемых элементов на основе детерминированной математической модели (окончание)
По мере возрастания нагрузки в местах трещин начинают появляться заметные неупругие деформации стальных волокон, свидетельствующие о приближении напряжений в волокнах к пределу текучести. Эпюра нормальных напряжений в фибробетоне сжатой зоны по мере увеличения нагрузки за счет развития неупругих деформаций постепенно искривляется. Величина максимальных напряжений постепенно перемещается с края в глубину сечения, а нулевая линия поднимается вверх. Эпюра нормальных напряжений растянутой зоны в месте образования трещин по мере увеличения нагрузки разбивается на локальные участки с повышенными значениями напряжений. Эти напряжения действуют в сечениях волокон, препятствующих росту и образованию трещин.
На третьей стадии разрушения фибробетонного элемента напряжения в фиброволокнах достигают физического или условного предела, когда волокно начинает либо вытягиваться из матрицы композита, либо при достижении предела прочности стали волокна рвётся (рис. 3, в); локальные участки повышенного напряжения становятся более выраженными. Выше нейтральной линии напряжения достигают временного сопротивления осевому сжатию. Здесь криволинейность эпюры нормальных напряжений сжатия также приближается по очертанию к кубической или параболе более высокого порядка.
Для проведения численного эксперимента и для практического использования предложенной математической модели была разработана программа для ЭВМ по оценке напряженно-деформированного состояния железобетонных и фибробетонных балок с учетом физической нелинейности конструкционных материалов SFRC (свидетельство о государственной регистрации программы для ЭВМ № 2016611439). Программа позволяет получить распределение напряжений по сечению на каждом этапе загружения с учетом влияния эксцентриситетов. Блок-схема алгоритма программы SFRC представлена на рис. 4, 5. Программа SFRC написана с помощью алгоритмического языка C++ в программной среде Builder Version 6.0 (Build 10.155).