В современной теории дифференциальных уравнений с частными производными теория локальных и нелокальных краевых задач для вырождающихся гиперболических и смешанного типов уравнений является одним из важнейших разделов, изучению которого посвящено немало публикаций. Повышенный интерес к уравнениям смешанного типа объясняется как теоретической значимостью получаемых результатов, так и многочисленными практическими приложениями в газовой динамике, теории бесконечно малых изгибаний поверхностей, в безмоментной теории оболочек, в магнитной гидродинамике, в теории электронного рассеивания, в математической биологии. Они имеют большое значение при математическом моделировании нефтяных пластов, фильтраций грунтовых вод, переноса тепла и массы в объекте, имеющего сложное строение электрических колебаний в проводах и других областях.
Анализ литературы по гиперболическим уравнениям переноса влаги в пористых средах показал, что наиболее адекватными реальной ситуации моделями являются математические модели, в основе которых лежит уравнение А.В. Лыкова с младшим членом, учитывающим движение почвенной влаги под действием гравитационных сил
Одномерный поток влаги в капиллярно-пористом теле поликапиллярной структуры u = u(ξ, t) связан с влажностью w = w(ξ, t) в точке ξ в момент времени t обобщенным законом переноса влаги
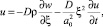
где D – коэффициент диффузии; ρ – плотность; a0 – коэффициент пропорциональности, зависящий от пористости тела, его капиллярных свойств и вязкости жидкости.
Если u и w связаны законом сохранения массы
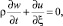
то получим систему дифференциальных уравнений. Производя замену
ρw = v; x = t/a0; y = ξ/a0,
а затем обозначив
a = –a0/D,
где a – безразмерная величина, придадим системе следующий вид:
y2ux + vy – au = 0; vx + uy = 0.
Дифференцируя первое по x, а второе по y и исключив v(x, y), получим уравнение А.В. Лыкова для определения u(x, y)
y2uxx – uyy + aux = 0.
Отметим, что это уравнение было приведено А.В. Бицадзе [1] как пример уравнения, для которого при 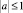 корректна по Адамару задача Коши с начальными данными на любом участке x0 < x < x1 линии y = 0 параболического вырождения, хотя нарушено известное условие Геллерстедта, а А.М. Нахушевым [6] как пример уравнения, для которого при
корректна по Адамару задача Коши с начальными данными на любом участке x0 < x < x1 линии y = 0 параболического вырождения, хотя нарушено известное условие Геллерстедта, а А.М. Нахушевым [6] как пример уравнения, для которого при 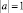 задача Дарбу не является корректной и характеристики не являются равноправными как носители граничных данных.
задача Дарбу не является корректной и характеристики не являются равноправными как носители граничных данных.
Цель исследования – доказать однозначную разрешимость задачи с дробными производными в краевом условии для вырождающегося гиперболического уравнения в характеристическом двуугольнике.
Постановка задачи. Рассмотрим уравнение влагопереноса
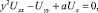 (1)
(1)
где a – действительная постоянная, причем 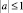 , в характеристическом двуугольнике, ограниченном характеристиками уравнения (1)
, в характеристическом двуугольнике, ограниченном характеристиками уравнения (1)
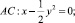
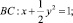
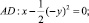
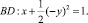
Пусть 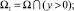
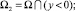 I – интервал 0 < x < 1 прямой y = 0.
I – интервал 0 < x < 1 прямой y = 0.
Задача: Найти решение
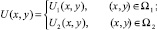
уравнения (1) из класса 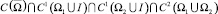 , удовлетворяющее условиям
, удовлетворяющее условиям
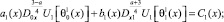 (2)
(2)
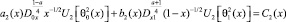 (3)
(3)
и условию сопряжения 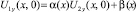 , где bi(x), ai(x), ci(x), α(x), β(x) – заданные функции, причем
, где bi(x), ai(x), ci(x), α(x), β(x) – заданные функции, причем 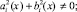 bi(x), ai(x), α(x),
bi(x), ai(x), α(x), 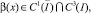 i = 1, 2,
i = 1, 2, 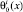 – точки пересечения характеристик уравнения (1), выходящих из точки (x, 0) ∈ I, с характеристиками AC, AD;
– точки пересечения характеристик уравнения (1), выходящих из точки (x, 0) ∈ I, с характеристиками AC, AD; 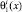 – точки пересечения характеристик уравнения (1), выходящих из точки (x, 0) с характеристиками BC, BD. Здесь и в дальнейшем
– точки пересечения характеристик уравнения (1), выходящих из точки (x, 0) с характеристиками BC, BD. Здесь и в дальнейшем 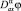 – операторы дробного в смысле Римана – Лиувилля интегро-дифференцирования порядка α с началом в точке a [3, 10].
– операторы дробного в смысле Римана – Лиувилля интегро-дифференцирования порядка α с началом в точке a [3, 10].
Доказательство единственности решения. Введем обозначения
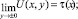
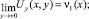
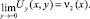
Решение задачи Коши для уравнения (1) при 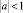 имеет вид [1]
имеет вид [1]
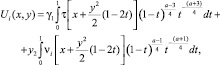 (4)
(4)
где i = 1, 2; 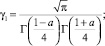
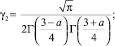 Г(α) – гамма-функция Эйлера [3].
Г(α) – гамма-функция Эйлера [3].
Удовлетворяя (4) краевым условиям (2) (3), получим соотношения между τ(x) и vi(x), принесенные на 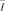 из областей Ω1 и Ω1 соответственно
из областей Ω1 и Ω1 соответственно
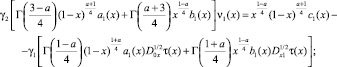 (5)
(5)
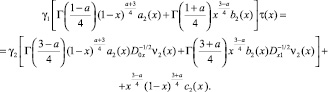 (6)
(6)
Теорема. В области Ω не может существовать более одного решения задачи (1)–(3), если либо
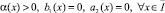 , (7)
, (7)
либо α(x) ≡ 1,
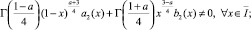 (8)
(8)
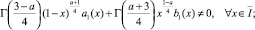 (9)
(9)
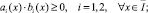 (10)
(10)
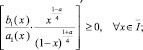 (11)
(11)
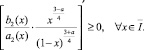 (12)
(12)
Доказательство. При ci(x) = 0 и выполнении условий (7) равенства (5), (6) примут вид
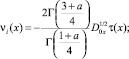
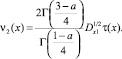
В силу принципа экстремума для гиперболических уравнений [1, 6] положительный максимум (отрицательный минимум) функции u(x, y) в 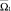 достигается на
достигается на 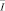 . Пусть положительный максимум функции u(x, y) достигается в точке (x, 0) ∈ I. Пользуясь тем, что дробные производные
. Пусть положительный максимум функции u(x, y) достигается в точке (x, 0) ∈ I. Пользуясь тем, что дробные производные 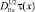 ,
, 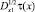 в точке положительного максимума строго положительны (в точке отрицательного минимума строго отрицательны) [6], получаем v1(x) < 0, v2(x) > 0. Это противоречит условию сопряжения при β(x) = 0, α(x) > 0.
в точке положительного максимума строго положительны (в точке отрицательного минимума строго отрицательны) [6], получаем v1(x) < 0, v2(x) > 0. Это противоречит условию сопряжения при β(x) = 0, α(x) > 0.
При ci(x) = 0 и выполнении условий (8), (9) равенства (5), (6) примут вид
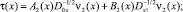
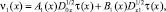
где
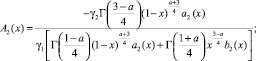
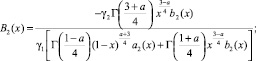
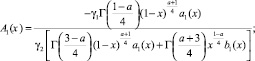
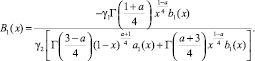
Рассмотрим интеграл
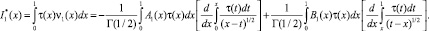
Вводя обозначения
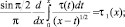
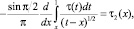
с учетом формулы обращения интегрального уравнения Абеля [3] получим
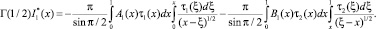
Воспользуемся известной формулой для функции Г(μ) [4]
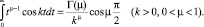
Полагая 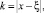 μ = 1/2 и поменяв порядок интегрирования, будем иметь
μ = 1/2 и поменяв порядок интегрирования, будем иметь
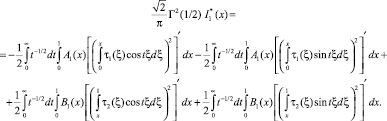
Отсюда, интегрируя по частям, с учетом того, что A1(1) = 0, B0(0) = 0, будем иметь
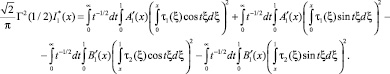
При выполнении условий (10), (11) теоремы единственности 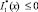 . Далее рассмотрим интеграл
. Далее рассмотрим интеграл
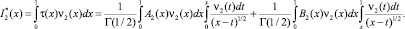
Последнее с учетом предыдущих вычислений представимо в виде
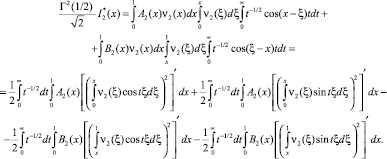
Так же, как и при вычислении интеграла 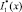 при выполнении условий (10), (12) теоремы единственности, нетрудно усмотреть, что
при выполнении условий (10), (12) теоремы единственности, нетрудно усмотреть, что 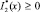 . Так как при α(x) = 1, β(x) = 1 будет v1(x) = v2(x), то
. Так как при α(x) = 1, β(x) = 1 будет v1(x) = v2(x), то
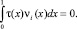
Следовательно,
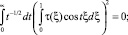
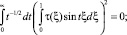
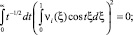
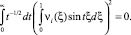
Из того, что t –1/2 ≥ 0, заключаем, что
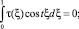
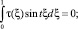
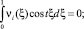
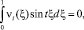
для всех t ∈ [0, ∞), в частности при t = 2πk, k = 0, 1, 2, .... При таких значениях t функции sin tξ и cos tξ образуют полную ортогональную систему функций в L2.
Таким образом, τ(x) = 0, vi(x) = 0, i = 1, 2 почти всюду. А так как эти функции непрерывны по условию, то τ(x) = 0 и vi(x) = 0 всюду. Отсюда Ui(x, y) = 0 в Ωi как решение задачи Коши с нулевыми данными и, следовательно, решение задачи (1)–(3) единственно.
Доказательство существования решения задачи. Исключая τ(x) из (5) и (6) при выполнении условий теоремы единственности и условий сопряжения, будем иметь
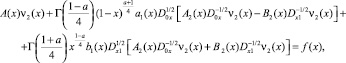 (13)
(13)
где 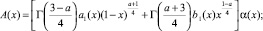
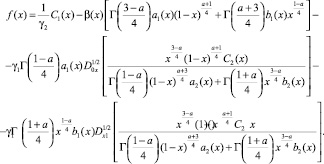
В результате преобразований вопрос существования решения уравнения (13) сведен к вопросу разрешимости сингулярного интегрального уравнения с ядром Коши [5].
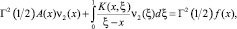 (14)
(14)
где 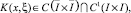
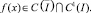
Условие
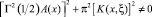
гарантирует существование регуляризатора, приводящего уравнение (14) к уравнению Фредгольма второго рода при A(x) ≠ 0.
Из возможности приведения задачи к эквивалентному интегральному уравнению Фредгольма второго рода и единственности искомого решения следует существование решения поставленной задачи. По найденному v2(x) определяется v1(x), а затем τ(x) и решения Ui(x, y) (i = 1, 2) задачи в областях Ωi, как решение задачи Коши по формуле (4). Нелокальные задачи для вырождающихся гиперболических и смешанного типов уравнений исследовались также в работах [2, 7–9].



