Теория локальных и нелокальных краевых задач для уравнений смешанного типа является одним из актуальных направлений уравнений в частных производных, изучению которого посвящено немало публикаций. Актуальность этих исследований можно обосновать внутренними потребностями теоретического обобщения классических задач для уравнений математической физики, получением новых результатов в теории дробного интегро-дифференцирования, а также их прикладным значением.
Цель исследования – доказать однозначную разрешимость задачи с дробными производными в краевом условии для уравнения смешанного типа третьего порядка с кратными характеристиками.
Постановка задачи
Рассматривается уравнение
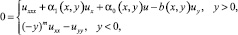(1)
где m = const > 0, в конечной области ?, ограниченной отрезками AA0, BB0, A0B0 прямых x = 0, x = 1, y = 1 соответственно, и характеристиками AC, BC равнения (1), выходящими из точек A(0;0), B(1;0) при y < 0.
Пусть Ω1 = Ω∩(y > 0); Ω2 = Ω∩(y < 0), I ≡ AB – единичный интервал 0 < x < 1 прямой y = 0.
Задача. Требуется определить функцию u(x, y), являющуюся решением уравнения (1) при y ≠ 0 из класса
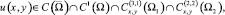
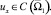
удовлетворяющую условиям
u(0, y) = φ1(y); u(1, y) = φ2(y), 0 ≤ y ≤ 1; (2)
u(0, y) – ux(1, y) = φ3(y), 0 ≤ y ≤ 1, (3)
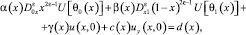
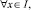(4)
где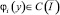 
(i = 1, 2, 3);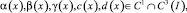 
причём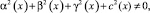 
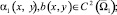
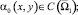
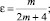
θ0(x), θ1(x) – точки пересечения характеристик уравнения (1), выходящих из точки (x, 0) с характеристиками AC, BC соответственно,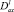 
– операторы дробного в смысле Римана – Лиувилля интегро-дифференцирования [9].
Задача (1)–(4) относится к классу краевых задач со смещением А.М. Нахушева, исследованиями которых занимались многие авторы [1–8, 10]. Интерес к таким задачам обусловлен тем, что они существенно обобщают задачу Трикоми, содержат широкий класс корректных самосопряженных задач и имеют многомерные аналоги.
Теорема единственности
В области Ω не может существовать более одного решения задачи (1)–(4), если
2a0(x, y) – a1x(x,y) + by(x, y) – 2b(x,y)N > 0 в Ω1; (5)
b(x, y) > ρ > 0; b(x,0) = const; (6)
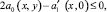(7)
где N – некоторая постоянная, удовлетворяющая условию
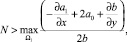
а также выполняются условия
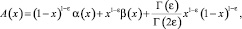
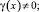(8)
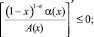
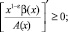
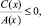
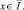(9)
Доказательство. Решение задачи Коши в области Ω2 имеет вид [1, 4]
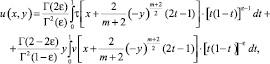(10)
где τ(x) = u(x, 0); v(x) = uy(x,0), Г(α) – гамма функция Эйлера [9].
Пользуясь решением (4), вычислим
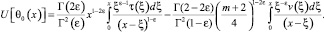
Последнее в терминах операторов дробного интегро-дифференцирования примет вид
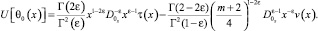
Аналогично, получаем
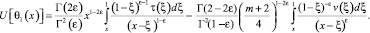
Последнее в терминах операторов дробного интегро-дифференцирования примет вид
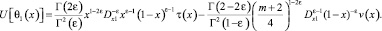
Подставляя значения, U[θ0(x)], U[θ1(x)] в условие (4), получим
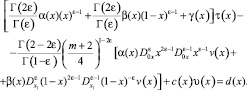(11)
Преобразовав интегралы, входящие в (11), будем иметь
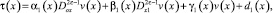(12)
где
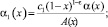
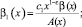
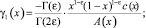
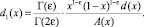
Докажем, что решение задачи (1)–(4) единственно при выполнении условий (5)–(9) теоремы. Для этого при d(x) = 0 покажем, что интеграл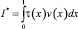 
не может быть отрицательным.
Действительно,
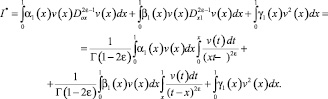
Используя методику, примененную в работах [5, 7], получим при y < 0
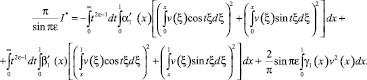(13)
Очевидно I* ≥ 0, если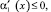 
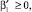γ1(x) ≥ 0. Таким образом, при выполнении условий (8)–(9) теоремы единственности I* ≥ 0.
Далее перейдём в уравнении (1) к пределу при y → +0. Будем иметь
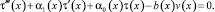(14)
Выражая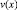 
из (14), находим
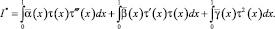
где
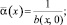
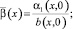
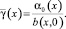
Или, что то же самое
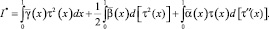
Отсюда, интегрируя по частям, нетрудно получить
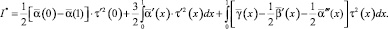
При выполнении условий (5)–(7) теоремы I* ≤ 0 при условиях (8), (9) I* ≥ 0. Следовательно, можно заключить, что I* = 0. Таким образом, левая часть (13) равна нулю. Поскольку слагаемые справа неотрицательны, то они также равны нулю. В частности,
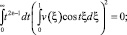
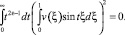
Так как t2ε–1 ≥ 0, то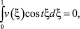 
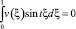для всех t ∈ (0, ∞), в частности при t = 2πk, k = 0, 1, 2, …
При этих значениях t функции sin tξ, cos tξ образуют полную ортогональную систему функций в L2. Следовательно, v(ξ) = 0 почти всюду, а так как ν(x) непрерывно по условию, то v(ξ) = 0 всюду. Отсюда легко заключить, что ν(x) = 0 и при d(x) = 0 из (11) имеем τ(x) = 0. Таким образом, U(x, y) ≡ 0 в Ω2 как решение задачи Коши с нулевыми данными, а в Ω1 как решение задачи (1)–(3) с нулевыми данными. Единственность решения задачи (1)–(4) при выполнении условий теоремы доказана.
Для доказательства существования решения задачи трижды проинтегрируем от 0 до x равенство (14). Получим
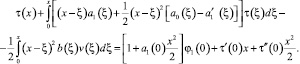(15)
Таким образом, соотношения между τ(x) и ν(x), принесённые из областей Ω1 и Ω2, имеют соответственно вид (15) и (12). Подставим τ(x) из (12) в (15). Получим
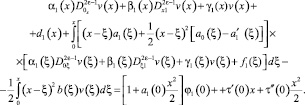
Последнее в результате преобразований примет вид
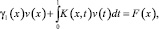(16)
где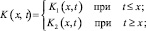 
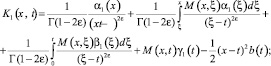
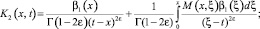
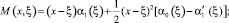
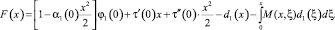
Уравнение (16) при γ1(x) ≠ 0 есть интегральное уравнение Фредгольма второго рода, первая часть которого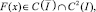 
а ядро 
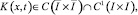при x ≠ t, а при x = t допускает оценку 
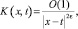где O(1) – ограниченная величина. Безусловная разрешимость уравнения (16) в требуемом классе функций заключается из единственности решения задачи. Решение уравнения (16) может быть найдено по формуле
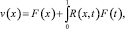
где К(x, t) – резольвента ядра K(x, t).