Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Кумыкова С.К. 1 Езаова А.Г. 1 Бозиева А.А. 1

---

1 Кабардино-Балкарский государственный университет им. Х.М. Бербекова

Настоящая статья посвящена исследованию однозначной разрешимости нелокальной задачи с дробными производными в краевом условии, для уравнения смешанного типа третьего порядка с кратными характеристиками. При ограничениях неравенственного типа на известные функции доказана теорема единственности. Доказательство теоремы проводится методом интегралов энергии. При доказательстве единственности решения задачи установлен эффект влияния коэффициента при младшей производной в уравнении на однозначную разрешимость поставленной краевой задачи. Для доказательства существования решения поставленной задачи получены соотношения между следом искомой функции u(x, 0) = (x) и следом производной искомой функции uy(x, 0) = v(x), принесенные на линию вырождения y = 0 из гиперболической и параболической частей смешанной области. Методом Трикоми существование решения задачи эквивалентно редуцированно к интегральному уравнению Фредгольма второго рода относительно следа производной искомой функции, безусловная разрешимость которого следует из единственности решения поставленной задачи.

Статья в формате PDF

0 KB

нелокальная задача

оператор дробного дифференцирования

оператор дробного интегрирования

задача Коши

уравнение Фредгольма

1. Бицадзе А.В. Некоторые классы уравнений в частных производных. – М.: Наука, 1981. –448 с.

2. Джураев Т.Д. Краевые задачи для уравнений смешанного и смешанно-составного типов. –Ташкент: ФАН, 1979.

3. Кумыкова С.К. Об одной задаче с нелокальными краевыми условиями на характеристиках для уравнения смешанного типа // Дифференциальные уравнения. – 1974. – Т.10. – № 1. – C. 78–88.

4. Нахушев А.М. Задачи со смещением для уравнений в частных производных. – М.: Наука, 2006. – 287 с.

5. Репин О.А., Кумыкова С.К. Задача со смещением для уравнения третьего порядка с разрывными коэффициентами // Вестник Самарского государственного технического университета. Серия «Физико-математические науки». – 2012. – № 4(29). – С. 150–158.

6. Репин О.А., Кумыкова С.К. О задаче с обобщенными операторами дробного дифференцирования для уравнения смешанного типа с двумя линиями вырождения // Вестник Самарского государственного технического университета. Серия «Физико-математические науки». – 2013. – № 1(30). – С. 150–158.

7. Репин О.А., Кумыкова С.К. Нелокальная задача для уравнения смешанного типа третьего порядка с обобщенными операторами дробного интегро-дифференцирования произвольного порядка // Вестник Самарского государственного технического университета. Естественнонаучная серия. – 2012. – № 9(100). – С. 52–60.

8. Салахитдинов М.С. Уравнения смешанно-составного типа. – Ташкент: ФАН,1974. – 155 с.

9. Самко С.Г., Килбас А.А., Маричев О.И. Интегралы и производные дробного порядка и некоторые их приложения. – Минск: Наука и техника, 1987. – 688 с.

10. Шогенов В.Х., Кумыкова С.К., Шхануков М.Х. Обобщенное уравнение переноса и дробные производные // Доклады национальной академии наук Украины. – 1997. – № 12. – С. 47–54.

Теория локальных и нелокальных краевых задач для уравнений смешанного типа является одним из актуальных направлений уравнений в частных производных, изучению которого посвящено немало публикаций. Актуальность этих исследований можно обосновать внутренними потребностями теоретического обобщения классических задач для уравнений математической физики, получением новых результатов в теории дробного интегро-дифференцирования, а также их прикладным значением.

Цель исследования – доказать однозначную разрешимость задачи с дробными производными в краевом условии для уравнения смешанного типа третьего порядка с кратными характеристиками.

Постановка задачи

Рассматривается уравнение

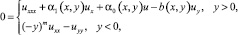(1)

где m = const > 0, в конечной области ?, ограниченной отрезками AA0, BB0, A0B0 прямых x = 0, x = 1, y = 1 соответственно, и характеристиками AC, BC равнения (1), выходящими из точек A(0;0), B(1;0) при y < 0.

Пусть Ω1 = Ω∩(y > 0); Ω2 = Ω∩(y < 0), I ≡ AB – единичный интервал 0 < x < 1 прямой y = 0.

Задача. Требуется определить функцию u(x, y), являющуюся решением уравнения (1) при y ≠ 0 из класса

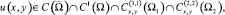
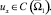
удовлетворяющую условиям

u(0, y) = φ1(y); u(1, y) = φ2(y), 0 ≤ y ≤ 1; (2)

u(0, y) – ux(1, y) = φ3(y), 0 ≤ y ≤ 1, (3)

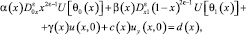
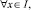(4)

где 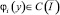(i = 1, 2, 3);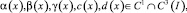

причём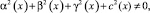

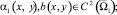
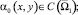
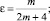
θ0(x), θ1(x) – точки пересечения характеристик уравнения (1), выходящих из точки (x, 0) с характеристиками AC, BC соответственно, 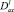– операторы дробного в смысле Римана – Лиувилля интегро-дифференцирования [9].

Задача (1)–(4) относится к классу краевых задач со смещением А.М. Нахушева, исследованиями которых занимались многие авторы [1–8, 10]. Интерес к таким задачам обусловлен тем, что они существенно обобщают задачу Трикоми, содержат широкий класс корректных самосопряженных задач и имеют многомерные аналоги.

Теорема единственности

В области Ω не может существовать более одного решения задачи (1)–(4), если

2a0(x, y) – a1x(x,y) + by(x, y) – 2b(x,y)N > 0 в Ω1; (5)

b(x, y) > ρ > 0; b(x,0) = const; (6)

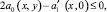(7)

где N – некоторая постоянная, удовлетворяющая условию

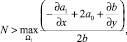
а также выполняются условия

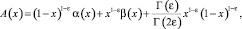
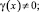(8)

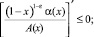
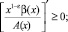
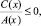
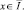(9)

Доказательство. Решение задачи Коши в области Ω2 имеет вид [1, 4]

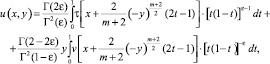(10)

где τ(x) = u(x, 0); v(x) = uy(x,0), Г(α) – гамма функция Эйлера [9].

Пользуясь решением (4), вычислим

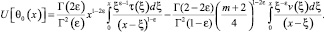
Последнее в терминах операторов дробного интегро-дифференцирования примет вид

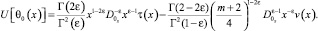
Аналогично, получаем

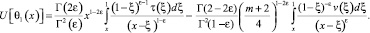
Последнее в терминах операторов дробного интегро-дифференцирования примет вид

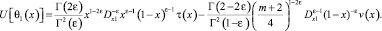
Подставляя значения, U[θ0(x)], U[θ1(x)] в условие (4), получим

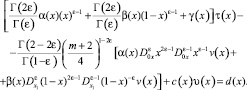(11)

Преобразовав интегралы, входящие в (11), будем иметь

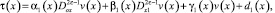(12)

где

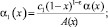
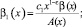
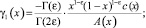
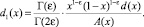
Докажем, что решение задачи (1)–(4) единственно при выполнении условий (5)–(9) теоремы. Для этого при d(x) = 0 покажем, что интеграл 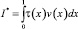не может быть отрицательным.

Действительно,

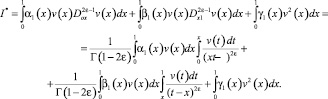
Используя методику, примененную в работах [5, 7], получим при y < 0

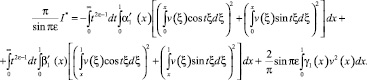(13)

Очевидно I* ≥ 0, если 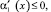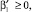γ1(x) ≥ 0. Таким образом, при выполнении условий (8)–(9) теоремы единственности I* ≥ 0.

Далее перейдём в уравнении (1) к пределу при y → +0. Будем иметь

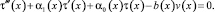(14)

Выражая 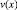из (14), находим

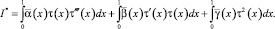
где

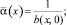
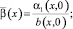
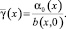
Или, что то же самое

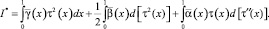
Отсюда, интегрируя по частям, нетрудно получить

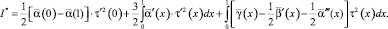
При выполнении условий (5)–(7) теоремы I* ≤ 0 при условиях (8), (9) I* ≥ 0. Следовательно, можно заключить, что I* = 0. Таким образом, левая часть (13) равна нулю. Поскольку слагаемые справа неотрицательны, то они также равны нулю. В частности,

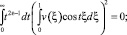
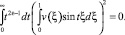
Так как t2ε–1 ≥ 0, то 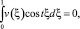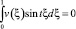для всех t ∈ (0, ∞), в частности при t = 2πk, k = 0, 1, 2, …

При этих значениях t функции sin tξ, cos tξ образуют полную ортогональную систему функций в L2. Следовательно, v(ξ) = 0 почти всюду, а так как ν(x) непрерывно по условию, то v(ξ) = 0 всюду. Отсюда легко заключить, что ν(x) = 0 и при d(x) = 0 из (11) имеем τ(x) = 0. Таким образом, U(x, y) ≡ 0 в Ω2 как решение задачи Коши с нулевыми данными, а в Ω1 как решение задачи (1)–(3) с нулевыми данными. Единственность решения задачи (1)–(4) при выполнении условий теоремы доказана.

Для доказательства существования решения задачи трижды проинтегрируем от 0 до x равенство (14). Получим

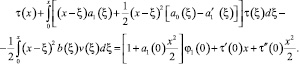(15)

Таким образом, соотношения между τ(x) и ν(x), принесённые из областей Ω1 и Ω2, имеют соответственно вид (15) и (12). Подставим τ(x) из (12) в (15). Получим

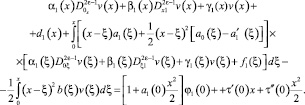
Последнее в результате преобразований примет вид

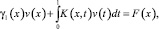(16)

где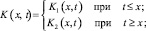

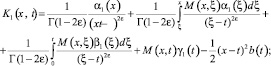
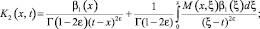
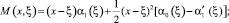
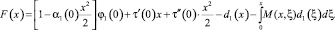
Уравнение (16) при γ1(x) ≠ 0 есть интегральное уравнение Фредгольма второго рода, первая часть которого 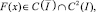а ядро 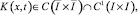при x ≠ t, а при x = t допускает оценку 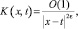где O(1) – ограниченная величина. Безусловная разрешимость уравнения (16) в требуемом классе функций заключается из единственности решения задачи. Решение уравнения (16) может быть найдено по формуле

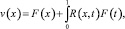
где К(x, t) – резольвента ядра K(x, t).

Библиографическая ссылка