В различных химико-технологических процессах широко используются оптические методы бесконтактного контроля. Особенно актуальны эти методы в химии полимеров для диагностики характеристик наноразмерных частиц. Нелинейно-оптическая диагностика наноматериалов основана на различных механизмах светоиндуцированной модуляции оптических констант среды. В наногетерогенной среде с различными показателями преломления компонентов на микрочастицы в электромагнитном поле действуют электрострикционные силы, которые могут быть причиной возникновения концентрационных потоков [1–4]. В зависимости от знака поляризуемости микрочастицы могут втягиваться (если показатель преломления вещества дисперсной фазы больше, чем дисперсионной среды) или выталкиваться (в обратном случае) из областей с большей напряженностью электрического поля электромагнитной волны.
Целью данной работы является теоретический анализ светолинзового отклика в прозрачной дисперсной среде при больших интенсивностях излучения, когда, в отличие от работы [5], изменение концентрации не обязательно мало.
Мы будем рассматривать жидкофазную среду с наночастицами (дисперсная фаза), находящуюся под воздействием лазерного излучения с гауссовым профилем интенсивности [5].
Для гауссова пучка распределение интенсивности падающего излучения в плоскости, перпендикулярной оптической оси z:
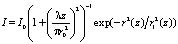, (1)
где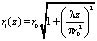 
– радиус пучка на расстоянии z от перетяжки, r – расстояние от оси пучка, ? – длина волны излучения, r0 – радиус пучка в перетяжке, I0 – интенсивность излучения на оси в плоскости перетяжки пучка.
Балансное уравнение, описывающее динамику концентрации наночастиц в жидкофазной среде с учётом диффузионного и электрострикционного потоков (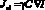
– электрострикционный поток), можно записать в виде [5]:
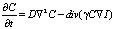. (2)
Здесь приняты следующие обозначения: C(r, t) – объемная концентрация дисперсных частиц, D – коэффициент диффузии, ? = b, ?,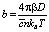 
, 
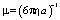– подвижность микрочастицы, а – размер частицы, ? – вязкость жидкости, ? – поляризуемость частиц, kB – постоянная Больцмана, n – эффективный показатель преломления среды, 
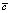– скорость света в вакууме.
В стационарном режиме уравнение (2) упрощаетcя:
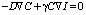. (3)
Общее решение уравнения (3) ищем в виде
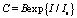, (4)
где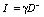 
, B – нормировочная константа. Данный результат показывает, что концентрация экспоненциально зависит от интенсивности (в отличие от обычной кубичной нелинейности) [1–6]. Введем безразмерный параметр интенсивности излучения 
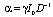. Для немалых изменений концентрации частиц (при большой интенсивности излучения) имеем ?>>1. Константу B находим из условия нормировки (сохранения числа частиц)
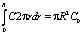, (5)
где R – радиус цилиндрической кюветы.
Для оптической силы концентрационной линзы имеем из (4–5) выражение [2]:
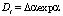, (6)
где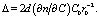 
Для частиц с радиусом, много меньшим длины волны излучения l, показатель преломления среды пропорционален концентрации частиц [5]:
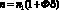, (7)
где ? = (n2 – n1)/n1); n1 и n2 – показатели преломления вещества дисперсионной среды и дисперсной фазы соответственно, Ф = (4/3)?a3C – объемная доля дисперсной среды.
Для расчета светолинзового сигнала используем выражение для линзовой прозрачности кюветы [1]:
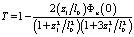(8)
где Фnl(0) – нелинейный набег фаз в оптической ячейке на оси пучка.
Используя (6–8), можем получить для стационарного значения нелинейного набега фазы:
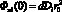. (9)
Полученное выражение позволяет определить концентрацию дисперсных наночастиц по светолинзовому отклику (8).
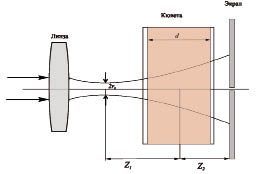
Однолучевая схема нелинейно-оптического эксперимента