1
Кирюшина С.И. 1 Мяготин А.В. 1
1 ФГБОУ ВПО «Дальневосточный государственный университет путей сообщения»
Метод нелинейной линзы широко используется в аналитической химии для оптической диагностики материалов. В дисперсной среде существует специфический механизм оптической нелинейности, основанный на перераспределении концентрации частиц дисперсной среды в градиентном световом поле. Для малых интенсивностей излучения потенциальная энергия частиц в световом поле меньше тепловой и изменение концентрации частиц пропорционально интенсивности и мало по сравнению с начальной. При этом описание нелинейно-оптических эффектов можно проводить в рамках обычного кубичного нелинейного отклика среды. Для более высоких интенсивностей необходимо решать уравнения массопереноса в световом поле. В данной работе проведен теоретический анализ светоиндуцированного массопереноса в дисперсной жидкофазной среде для больших интенсивностей излучения в поле гауссова пучка, когда изменение концентрации больше или сравнимо с начальной. Показано, что самовоздействие излучения происходит в существенно нелинейном режиме. Нелинейная линза в этом режиме экспоненциально растет с увеличением интенсивности излучения. Полученные результаты актуальны при исследовании самовоздействия излучения в дисперсных жидкофазных средах, а также для оптической диагностики таких сред, в т.ч. оптической спектроскопии.
самовоздействие излучения
электрострикция
дисперсная среда
1. Иванов В.И., Иванова Г.Д., Хе В.К. Влияние термодиффузии на термолинзовый отклик в жидкофазной дисперсной среде// Физико-химические аспекты изучения кластеров, наноструктур и наноматериалов, межвуз. сб. науч. тр. / под общей редакцией В.М. Самсонова, Н.Ю. Сдобнякова. – Тверь: Твер. гос. ун-т, 2013. – Вып. 5. – С. 112–115.
2. Иванов В.И., Кузин А.А., Ливашвили А.И., Хе В.К. Динамика светоиндуцированной тепловой линзы в жидкофазной двухкомпонентной среде // Научно-технические ведомости Санкт-Петербургского государственного политехнического университета. Физико-математические науки. – 2011. – Т. 4, № 134. – С. 44–46.
3. Иванов В.И., Кузин А.А., Окишев К.Н. Оптическая левитация наночастиц: монография. – Хабаровск: Изд-во ДВГУПС, 2008. – 105 с.
4. Иванов В.И., Кузин А.А., Окишев К.Н. Термодиффузионный механизм самомодуляции излучения в среде с поглощающими наночастицами // Известия высших учебных заведений. Физика. – 2009. – Т. 52, № 12–3. – С. 114–116.
5. Иванов В.И., Ливашвили А.И. Термодиффузионный механизм самовоздействия излучения в среде с наночастицами // Известия высших учебных заведений. Физика. – 2009. – Т. 52, № 12–3. – С. 117–119.
6. Иванов В.И., Ливашвили А.И. Электрострикционный механизм самовоздействия излучения в жидкости с наночастицами// Вестник Новосибирского государственного университета. Серия: Физика. – 2009. – Т. 4, № 2. – С. 58–60.
7. Иванов В.И., Ливашвили А.И. Эффект Дюфура в дисперсной жидкофазной среде в поле гауссова пучка // Физико-химические аспекты изучения кластеров, наноструктур и наноматериалов, межвуз. сб. науч. тр. / под общей редакцией В.М. Самсонова, Н.Ю. Сдобнякова. – Тверь: Твер. гос. ун-т, 2013. – Вып. 5. – С. 116–119.
8. Иванов В.И., Ливашвили А.И., Окишев К.Н. Термодиффузионный механизм изменения оптического пропускания двухкомпонентной среды // Известия высших учебных заведений. Приборостроение. – 2008. – Т. 51, № 3. – С. 50–53.
9. Иванов В.И., Окишев К.Н., Карпец Ю.М., Ливашвили А.И. Термодиффузионный механизм просветления двухкомпонентной среды лазерным излучением // Известия Томского политехнического университета. – 2007. – Т. 311, № 2. – С. 39–42.
10. Окишев К.Н. Термодиффузионный механизм нелинейного поглощения суспензии наночастиц / К.Н. Окишев, В.И. Иванов, С.В. Климентьев, А.А. Кузин, А.И. Ливашвили // Оптика атмосферы и океана. – 2010. – Т. 23, № 2. – С. 106–107.
В различных химико-технологических процессах широко используются оптические методы бесконтактного контроля. Особенно актуальны эти методы в химии полимеров для диагностики характеристик наноразмерных частиц. Нелинейно-оптическая диагностика наноматериалов основана на различных механизмах светоиндуцированной модуляции оптических констант среды. В наногетерогенной среде с различными показателями преломления компонентов на микрочастицы в электромагнитном поле действуют электрострикционные силы, которые могут быть причиной возникновения концентрационных потоков [1–4]. В зависимости от знака поляризуемости микрочастицы могут втягиваться (если показатель преломления вещества дисперсной фазы больше, чем дисперсионной среды) или выталкиваться (в обратном случае) из областей с большей напряженностью электрического поля электромагнитной волны.
Целью данной работы является теоретический анализ светолинзового отклика в прозрачной дисперсной среде при больших интенсивностях излучения, когда, в отличие от работы [5], изменение концентрации не обязательно мало.
Мы будем рассматривать жидкофазную среду с наночастицами (дисперсная фаза), находящуюся под воздействием лазерного излучения с гауссовым профилем интенсивности [5].
Для гауссова пучка распределение интенсивности падающего излучения в плоскости, перпендикулярной оптической оси z:
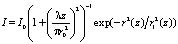 , (1)
, (1)
где 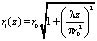 – радиус пучка на расстоянии z от перетяжки, r – расстояние от оси пучка, ? – длина волны излучения, r0 – радиус пучка в перетяжке, I0 – интенсивность излучения на оси в плоскости перетяжки пучка.
– радиус пучка на расстоянии z от перетяжки, r – расстояние от оси пучка, ? – длина волны излучения, r0 – радиус пучка в перетяжке, I0 – интенсивность излучения на оси в плоскости перетяжки пучка.
Балансное уравнение, описывающее динамику концентрации наночастиц в жидкофазной среде с учётом диффузионного и электрострикционного потоков (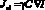 – электрострикционный поток), можно записать в виде [5]:
– электрострикционный поток), можно записать в виде [5]:
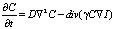 . (2)
. (2)
Здесь приняты следующие обозначения: C(r, t) – объемная концентрация дисперсных частиц, D – коэффициент диффузии, ? = b, ?, 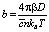 ,
, 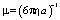 – подвижность микрочастицы, а – размер частицы, ? – вязкость жидкости, ? – поляризуемость частиц, kB – постоянная Больцмана, n – эффективный показатель преломления среды,
– подвижность микрочастицы, а – размер частицы, ? – вязкость жидкости, ? – поляризуемость частиц, kB – постоянная Больцмана, n – эффективный показатель преломления среды, 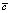 – скорость света в вакууме.
– скорость света в вакууме.
В стационарном режиме уравнение (2) упрощаетcя:
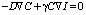 . (3)
. (3)
Общее решение уравнения (3) ищем в виде
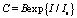 , (4)
, (4)
где 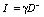 , B – нормировочная константа. Данный результат показывает, что концентрация экспоненциально зависит от интенсивности (в отличие от обычной кубичной нелинейности) [1–6]. Введем безразмерный параметр интенсивности излучения
, B – нормировочная константа. Данный результат показывает, что концентрация экспоненциально зависит от интенсивности (в отличие от обычной кубичной нелинейности) [1–6]. Введем безразмерный параметр интенсивности излучения 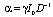 . Для немалых изменений концентрации частиц (при большой интенсивности излучения) имеем ?>>1. Константу B находим из условия нормировки (сохранения числа частиц)
. Для немалых изменений концентрации частиц (при большой интенсивности излучения) имеем ?>>1. Константу B находим из условия нормировки (сохранения числа частиц)
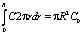 , (5)
, (5)
где R – радиус цилиндрической кюветы.
Для оптической силы концентрационной линзы имеем из (4–5) выражение [2]:
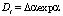 , (6)
, (6)
где 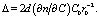
Для частиц с радиусом, много меньшим длины волны излучения l, показатель преломления среды пропорционален концентрации частиц [5]:
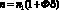 , (7)
, (7)
где ? = (n2 – n1)/n1); n1 и n2 – показатели преломления вещества дисперсионной среды и дисперсной фазы соответственно, Ф = (4/3)?a3C – объемная доля дисперсной среды.
Для расчета светолинзового сигнала используем выражение для линзовой прозрачности кюветы [1]:
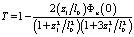 (8)
(8)
где Фnl(0) – нелинейный набег фаз в оптической ячейке на оси пучка.
Используя (6–8), можем получить для стационарного значения нелинейного набега фазы:
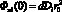 . (9)
. (9)
Полученное выражение позволяет определить концентрацию дисперсных наночастиц по светолинзовому отклику (8).
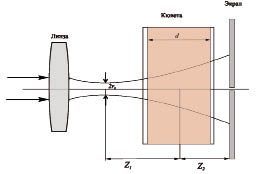
Однолучевая схема нелинейно-оптического эксперимента
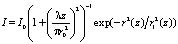 , (1)
, (1)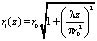 – радиус пучка на расстоянии z от перетяжки, r – расстояние от оси пучка, ? – длина волны излучения, r0 – радиус пучка в перетяжке, I0 – интенсивность излучения на оси в плоскости перетяжки пучка.
– радиус пучка на расстоянии z от перетяжки, r – расстояние от оси пучка, ? – длина волны излучения, r0 – радиус пучка в перетяжке, I0 – интенсивность излучения на оси в плоскости перетяжки пучка.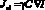 – электрострикционный поток), можно записать в виде [5]:
– электрострикционный поток), можно записать в виде [5]: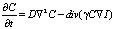 . (2)
. (2)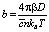 ,
, 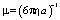 – подвижность микрочастицы, а – размер частицы, ? – вязкость жидкости, ? – поляризуемость частиц, kB – постоянная Больцмана, n – эффективный показатель преломления среды,
– подвижность микрочастицы, а – размер частицы, ? – вязкость жидкости, ? – поляризуемость частиц, kB – постоянная Больцмана, n – эффективный показатель преломления среды, 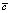 – скорость света в вакууме.
– скорость света в вакууме.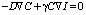 . (3)
. (3) 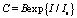 , (4)
, (4)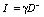 , B – нормировочная константа. Данный результат показывает, что концентрация экспоненциально зависит от интенсивности (в отличие от обычной кубичной нелинейности) [1–6]. Введем безразмерный параметр интенсивности излучения
, B – нормировочная константа. Данный результат показывает, что концентрация экспоненциально зависит от интенсивности (в отличие от обычной кубичной нелинейности) [1–6]. Введем безразмерный параметр интенсивности излучения 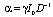 . Для немалых изменений концентрации частиц (при большой интенсивности излучения) имеем ?>>1. Константу B находим из условия нормировки (сохранения числа частиц)
. Для немалых изменений концентрации частиц (при большой интенсивности излучения) имеем ?>>1. Константу B находим из условия нормировки (сохранения числа частиц) 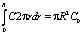 , (5)
, (5)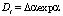 , (6)
, (6)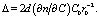
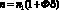 , (7)
, (7)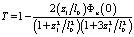 (8)
(8)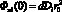 . (9)
. (9)



