Постановка задачи
Рассмотрим задачу о взрывном воздействии на сооружение, которое находится в грунтовой и водной средах.
Рассмотрим некоторое тело, состоящее из двух разных областей Г(1) (водная среда) и Г(2) (грунтовая среда) (рис. 1). Для решения задачи о моделировании волн напряжений в упругих деформируемых средах рассмотрим некоторое тело Г(1) в прямоугольной декартовой системе координат XOY, которому в начальный момент времени t = 0 сообщается механическое воздействие. Предположим, что тело Г(1) изготовлено из деформируемой водной среды и является однородным изотропным материалом, подчиняющимся упругому закону Гука при малых упругих деформациях. Если в деформируемом твердом теле, предположим, что поперечная скорость распространения равна нулю, то можно получить уравнения состояния для водной среды.
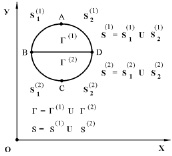
Рис. 1. Некоторое тело, состоящее из двух разных областей Г(1) и Г(2) в прямоугольной декартовой системе координат XOY
Точные уравнения двумерной плоской нестационарной динамической теории упругости для области Г(1) имеют вид
, 
,
,
,
,
, 
,
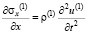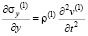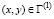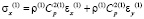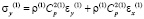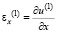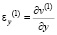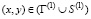, (1)
где 
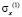и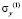 
– компоненты тензора упругих напряжени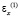й; 
и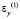 
– компоненты тензора упругих деформаций; u(1) и v(1) – cоставляющие вектора упругих перемещений вдоль осей OX и OY соответственно; ρ(1) – плотность материала; 
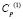– скорость продольной упругой волны; 
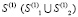– граничный контур тела Г(1).
Систему (1) в области, занимаемой телом Г(1), следует интегрировать при начальных и граничных условиях.
Точные уравнения двумерной плоской нестационарной динамической теории упругости для области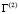 
имеют вид
,
, 
,
,
,
, 
,
,
, 
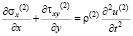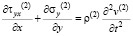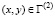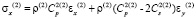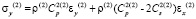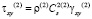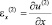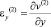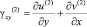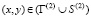, (2)
где 
, 
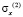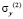и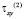 
– компоненты тензора упругих напряжени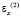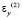й; 
, 
и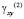 
– компоненты тензора упругих деформаций; u(2) и v(2) – cоставляющие вектора упругих перемещений вдоль осей OX и OY соответственно; ρ(2) – плотность материала;
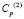– скорость продольной упругой волны; 
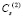– скорость поперечной упругой волны; 
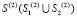– граничный контур тела Г(2).
Систему (2) в области, занимаемой телом Г(2), следует интегрировать при начальных и граничных условиях.
В работах [1–10] приведена информация о моделировании нестационарных волн напряжений в объектах сложной формы с помощью разработанного и применяемого численного метода, алгоритма и комплекса программ.
Численное решение двумерной плоской динамической задачи теории упругости
Для решения двумерной плоской нестационарной динамической задачи теории упругости с начальными и граничными условиями – используем метод конечных элементов в перемещениях.
Принимая во внимание определение матрицы жесткости, вектора инерции и вектора внешних сил для тела Г, записываем приближенное значение уравнения движения в нестационарной теории упругости
, 
, 
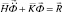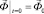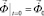, (3)
где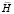 
– матрица инерции; 
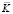– матрица жесткости; 
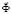– вектор узловых упругих перемещений; 
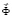– вектор узловых упругих скоростей перемещений; 
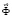– вектор узловых упругих ускорений; 
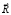– вектор узловых упругих внешних сил.
Интегрируя по временной координате соотношение (3) с помощью конечноэлементного варианта метода Галеркина, получим двумерную явную двухслойную конечноэлементную линейную схему в перемещениях для внутренних и граничных узловых точек
,
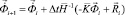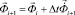(4)
Основные соотношения метода конечных элементов в перемещениях получены с помощью принципа возможных перемещений и конечноэлементного варианта метода Галеркина.
Шаг по временной переменной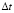 
определяем из следующего соотношения
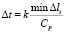
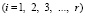, (5)
где Δl – длина стороны конечного элемента.
Результаты численного эксперимента показали, что при k = 0,5 обеспечивается устойчивость явной двухслойной схемы.
Информация о математической точности и физической достоверности разработанного численного метода, алгоритма и комплекса программ приведена в следующих работах [1–4].
Решение задачи о сосредоточенном взрывном воздействии на набережной речного порта с заполненным водным объектом на 25 %
Рассмотрим задачу о сосредоточенном упругом взрывном воздействии (рис. 3) на набережной речного порта с заполненным водным объектом на 25 % (рис. 2).
Рис. 2. Постановка задачи о сосредоточенном упругом взрывном воздействии на набережной речного порта с заполненным водным объектом на 25 %
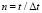) изменяется линейно от 0 до P, при 11 ≤ n ≤ 20 изменяется P до 0 (P = σ0, σ0 = – 0,1 МПа). Граничные условия для контура EFGHA при t > 0 
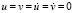. Отраженные волны от контура EFGHA не доходят до исследуемых точек при 0 ≤ n ≤ 200. Контур EDCBA свободен от нагрузок, кроме точки D, где приложено сосредоточенное взрывное воздействие. На границе BIH приняты условия непрерывности перемещений. Для области CDEFGHIB приняты следующие исходные данные: H = Δx = Δy; 
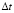= 1,393×10-6 с; E = 3,15× ×104 МПа; v = 0,2; ρ = 0,255×104 кг/м3; Cp = 3587 м/с; CS = 2269 м/с. Для области ABIH приняты следующие исходные данные: H = Δx = Δy; Δt = 1,327×10-5 с; ρ = 1,025×103 кг/м3; Cp = 1530 м/с. В расчетах принимается минимальный шаг по времени, то есть Δt = 1,393×10-6 с. Исследуемая расчетная область имеет 20402 узловые точки. Решается система уравнений из 81608 неизвестных.
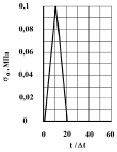
Рис. 3. Взрывное воздействие для задачи с заполненным водным объектом на 25 %
На рис. 4–7 показано изменение упругого контурного напряжения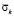 
(
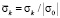) во времени n в точках A1–A4 (рис. 2), находящихся на свободной поверхности упругой полуплоскости.
Рис. 4. Изменение упругого контурного напряжения 
во времени t/Δt в точке A1 в задаче с заполненным водным объектом на 25 %
Рис. 5. Изменение упругого контурного напряжения 
во времени t/Δt в точке A2 в задаче с заполненным водным объектом на 25 %
Рис. 6. Изменение упругого контурного напряжения 
во времени t/Δt в точке A3 в задаче с заполненным водным объектом на 25 %
Рис. 7. Изменение упругого контурного напряжения 
во времени t/Δt в точке A4 в задаче с заполненным водным объектом на 25 %
Выводы
Заполненный водный объект на 25 % изменяет величину упругого растягивающего контурного напряжения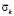 
в 1,00 раз. Заполненный водный объект на 25 % изменяет величину упругого сжимающего контурного напряжения 
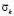в 1,00 раз. Заполненный водный объект на 25 % изменяет величину упругого растягивающего нормального напряжения 
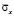в 1,00 раз. Заполненный водный объект на 25 % изменяет величину упругого сжимающего нормального напряжения 
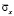в 1,00 раз.