Пусть малое тело массы m0 движется в поле тяготения центрального тела массы m1 и внешнего тела массы m2. Здесь m1 > m2 >> m0 и внешнего тело движется относительно центрального тела по окружности, тогда силовая функция плоской второй задачи Хилла имеет вид:
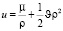 (1)
(1)
где 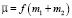 – гравитационная постоянная, v – постоянный параметр, х, у – координаты малого тела, ρ2 = x2 + y2.
– гравитационная постоянная, v – постоянный параметр, х, у – координаты малого тела, ρ2 = x2 + y2.
Силовая функция (1) учитывает поле тяготения шарообразного центрального тела и некоторую часть поля тяготения внешнего тела.
Выполнив замену переменных с учетом (1) дифференциальные уравнения движения малого тела можно записать в следующем виде:
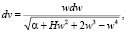
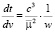 (2)
(2)
где 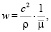
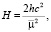
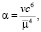
с – постоянная интеграла площадей,
h – постоянная интеграла энергий.
В работе [2] выполнена классификация типов движения:
1. Прямолинейное движение α = 0, H = 0, c = 0;
2. Параболический тип движения α > 0, H = 0;
3. Эллиптический тип движения α > 0, H < 0;
4. Гиперболический тип движения α > 0, H > 0;
5. Круговой тип движения α > 0, H < 0, e = 0;
где е – эксцентриситет орбиты пассивно гравитирующего тела.
Рассматриваем эллиптический тип движенияс привлечением эллиптических функции Якоби.
В случае эллиптического типа движения имеем α > 0, H < 0, поэтому дифференциальное уравнение (2) имеет вид:
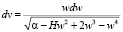 (3)
(3)
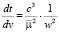 . (4)
. (4)
По теореме Декарта подкоренной полином G4(w) = α – Hw2 + 2w3 – w4 имеет три положительных корня α1, α2 α3 и один отрицательный. Полином положителен в двух интервалах: А. 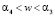 и В.
и В. 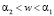 .
.
Интегрирование дифференциальных уравнений (3) и (4) было выполнено в статье [3]. Пользуясь этой методикой полярные координаты малого тела.
Интервал А (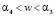 )
)
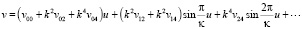 (5)
(5)
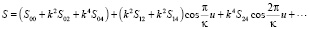 (6)
(6)
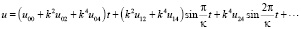 (7)
(7)
Все коэффициенты (5)–(7) определены в виде формул от корней полинома G4(w) = α – Hw2 + 2w3 – w4 и для краткости не будем их приводить.
Интервал В (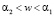 ).
).
Полярный угол и полярный радиус записаны точно такими же формулами, как и на интервале А, лишь с той разницей, что коэффиценты определены другими выражениями от корней полинома G4(w) = α – Hw2 + 2w3 – w4.
Из выражений (5–7) видно, что полярный радиус не содержит вековых членов, а полярный угол пропорционален времени. Но прямоугольные координаты
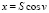 ,
, 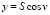
вековых членов не имеют, следовательно результаты приемлемы на достаточно большом промежутке времени сопоставимы с соответствующими интервалами А и В.
Найденные решения можно использовать в качестве промежуточной орбиты.



