Пусть пассивно гравитирующее тело массы m0 движется в поле тяготения центрального тела массы m1 и внешнего тела массы m2. Пусть m1 > m2 >> m0 и внешнего тело движется относительно центрального тела по окружности, тогда силовая функция плоской второй задачи Хилла имеет вид:
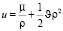 (1)
(1)
где 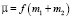 – гравитационная постоянная, v – постоянный параметр, х, у – координаты пассивно гравитирующего тела, ρ2 = x2 + y2.
– гравитационная постоянная, v – постоянный параметр, х, у – координаты пассивно гравитирующего тела, ρ2 = x2 + y2.
Силовая функция (1) учитывает поле тяготения шарообразного центрального тела и некоторую часть поля тяготения внешнего тела.
Выполнив замену переменных с учетом (1) дифференциальные уравнения движения пассивно гравитирующего тела можно записать в следующем виде:
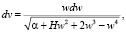
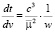 (2)
(2)
где 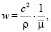
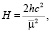
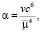
с – постоянная интеграла площадей,
h – постоянная интеграла энергий.
Варьируя параметры α и H найдем следующие типы движения пассивно гравитирующего тела во второй задаче Хилла:
1. Прямолинейное движение α = 0, H = 0.
2. Параболический тип движения α > 0, H = 0.
3. Эллиптический тип движения α > 0, H < 0.
4. Гиперболический тип движения α > 0, H > 0.
5. Круговой тип движения α > 0, H < 0, e = 0.
где e – эксцентриситет орбиты пассивно гравитирующего тела.
В случае гиперболического типа движения имеем α > 0, H > 0, поэтому (2) перепишем без изменения.
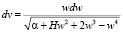
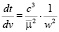 .
.
Подкоренной полином имеет четыре корня. Пользуясь теоремой и расширенной теоремой Декарта находим, что полином имеет один положительный и один отрицательный корень. На долю комплексных корней остается два корня. Обозначив положительный корень через α1, а отрицательный через α2 и комплексно сопряженные через 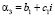 ,
, 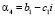 приходим к ситуации, которых у нас складывалось в случае параболического движения [3].
приходим к ситуации, которых у нас складывалось в случае параболического движения [3].
В реальных движениях 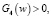 поэтому имеем два интервала которые составляют область возможности движения:
поэтому имеем два интервала которые составляют область возможности движения:
А: интервал 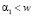 .
.
В: интервал 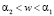 .
.
Рассмотрим далее первый интервал т.е. А, здесь уместно оставить обозначения без изменения, тогда в интервале 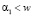 полярные координаты пассивно гравитирующего тела в случае А гиперболического типа движения определяется выражениями
полярные координаты пассивно гравитирующего тела в случае А гиперболического типа движения определяется выражениями
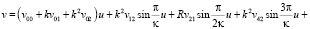
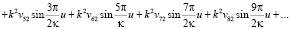 (3)
(3)
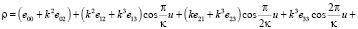
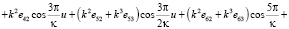
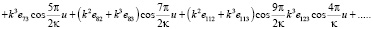 (4)
(4)
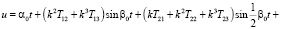
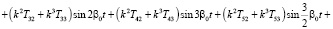
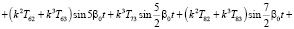
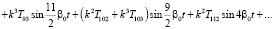 (5)
(5)
а в случае В на интервале 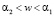 выражениями:
выражениями:
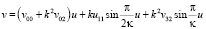
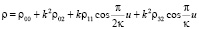
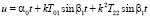
Здесь следует иметь в виду, что корни α1, α2, α3, α4 будут совершенно другими, чем при параболическом типе движения пассивно гравитирующего тела. В это можно убедиться определив методами алгебры границы этих корней в об их движениях.
Полученные решения пригодны и в случае малого наклона орбиты к основной плоскости. Кроме этого решения в позиционных координатах не имеют вековых членов. Используя (3) и (5) можно решить пространственную вторую задачу Хилла в случае малого наклона орбиты к основной плоскости.
Таким образом для плоской задачи Хилла найдены полярные координаты пассивно гравитирующего тела в случае гиперболического типа движения на интегралах 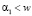 ,
, 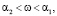 как явные функции времени.
как явные функции времени.
Полученные решения представляют собой новую плоскую промежуточную орбиту ИЗС.



