Пусть пассивно гравитирующее тело массы m0 движется в поле тяготения центрального тела массы m1 и внешнего тела массы m2. Пусть m1 > m2 >> m0 и внешнего тело движется относительно центрального тела по окружности, тогда силовая функция плоской второй задачи Хилла имеет вид:
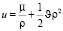 (1)
(1)
где 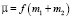 – гравитационная постоянная, v – постоянный параметр, х, у – координаты пассивно гравитирующего тела, ρ2 = x2 + y2.
– гравитационная постоянная, v – постоянный параметр, х, у – координаты пассивно гравитирующего тела, ρ2 = x2 + y2.
Силовая функция (1) учитывает поле тяготения шарообразного центрального тела и некоторую часть поля тяготения внешнего тела.
Выполнив замену переменных с учетом (1) дифференциальные уравнения движения пассивно гравитирующего тела можно записать в следующем виде:
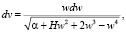
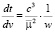 (2)
(2)
где 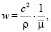
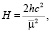
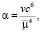
с – постоянная интеграла площадей,
h – постоянная интеграла энергий.
Варьируя параметры α и H найдем следующие типы движения пассивно гравитирующего тела во второй задаче Хилла:
1. Прямолинейное движение α = 0, H = 0.
2. Параболический тип движения α > 0, H = 0.
3. Эллиптический тип движения α > 0, H < 0.
4. Гиперболический тип движения α > 0, H > 0.
5. Круговой тип движения α > 0, H < 0, e = 0.
где e – эксцентриситет орбиты пассивно гравитирующего тела.
В случае гиперболического типа движения имеем α > 0, H > 0, поэтому (2) перепишем без изменения.
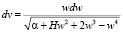
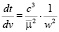 .
.
Подкоренной полином имеет четыре корня. Пользуясь теоремой и расширенной теоремой Декарта находим, что полином имеет один положительный и один отрицательный корень. На долю комплексных корней остается два корня. Обозначив положительный корень через α1, а отрицательный через α2 и комплексно сопряженные через 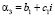 ,
, 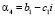 приходим к ситуации, которых у нас складывалось в случае параболического движения [3].
приходим к ситуации, которых у нас складывалось в случае параболического движения [3].
В реальных движениях 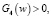 поэтому имеем два интервала которые составляют область возможности движения:
поэтому имеем два интервала которые составляют область возможности движения:
А: интервал 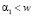 .
.
В: интервал 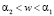 .
.
Рассмотрим далее первый интервал т.е. А, здесь уместно оставить обозначения без изменения, тогда в интервале 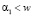 полярные координаты пассивно гравитирующего тела в случае А гиперболического типа движения определяется выражениями
полярные координаты пассивно гравитирующего тела в случае А гиперболического типа движения определяется выражениями
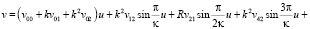
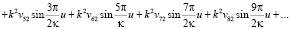 (3)
(3)
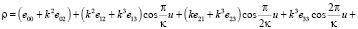
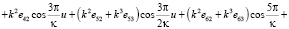
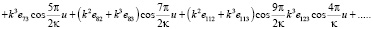 (4)
(4)
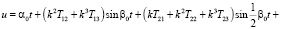
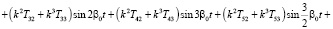
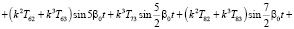
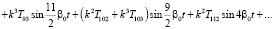 (5)
(5)
а в случае В на интервале 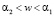 выражениями:
выражениями:
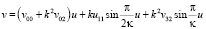
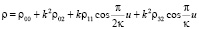
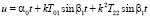
Здесь следует иметь в виду, что корни α1, α2, α3, α4 будут совершенно другими, чем при параболическом типе движения пассивно гравитирующего тела. В это можно убедиться определив методами алгебры границы этих корней в об их движениях.
Полученные решения пригодны и в случае малого наклона орбиты к основной плоскости. Кроме этого решения в позиционных координатах не имеют вековых членов. Используя (3) и (5) можно решить пространственную вторую задачу Хилла в случае малого наклона орбиты к основной плоскости.
Таким образом для плоской задачи Хилла найдены полярные координаты пассивно гравитирующего тела в случае гиперболического типа движения на интегралах 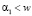 ,
, 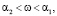 как явные функции времени.
как явные функции времени.
Полученные решения представляют собой новую плоскую промежуточную орбиту ИЗС.
Библиографическая ссылка
Жапбаров С.А., Ажибеков К.Ж., Ермаханов М.Н., Бесбаев Г.А., Курымбаева Н., Бекболатова С.С. ГИПЕРБОЛИЧЕСКИЙ ТИП ДВИЖЕНИЯ ПАССИВНО ГРАВИТИРУЮЩЕГО ТЕЛА ВО ВТОРОЙ ЗАДАЧЕ ХИЛЛА // Современные наукоемкие технологии. 2015. № 1-1. С. 59-61;URL: https://top-technologies.ru/ru/article/view?id=34993 (дата обращения: 01.03.2026).



