Известно, что энергия разрыва связи между атомами (E) в основном определяется их межъядерным расстоянием. Существует большое число уравнений, связывающих величину энергии разрыва и длину связи (ℓ) между атомами, находящимися в одном и том же состоянии гибридизации. Считалось, что для атомов, находящихся в различных состояниях гибридизации, необходимо учитывать не только длину связи, но и изменение её характерной особенности. Следует отметить, что до настоящего времени нет достаточно четкого представления о взаимосвязи энергии разрыва связи с электронным строением атомов.
Результаты исследования и их обсуждение
Зависимость энергии разрыва от гибридизации для разных атомов в ряде случаев не однотипна. Так, в табл. 1 приведены значения энергий диссоциации четырех элемент-элементных связей, приведенных в литературных источниках [2, 4, 7, 8].
Из приведенных данных следует:
– в этане σ-связь наиболее прочная, в молекуле Э уступает σ-связи на 20 ккал/моль. В ацетилене π-связь энергетически еще меньше (58,5 ккал/моль);
– подобная последовательность в изменении энергий связи наблюдается в соединениях фосфора;
– противоположная последовательность изменения параметров, характеризующих прочность связи, наблюдается в соединениях азота и кислорода. Для них характерно последовательное повышение энергии от σ- к π-связям, вместе с тем двойные и тройные связи, образованные атомами азота, обладают большими энергиями π-связей, чем удвоенные и утроенные значения соответствующей σ-связи.
Отношение энергии π-связи к энергии σ-связи > 1 имеет место и для О–О-связи. Однако для связей С–С, Р–Р, Р–О, S–S и др. отношение энергия π-связи к энергии σ-связи < 1. Для связей С–О, С–N, P–N это отношение близко к единице. Поэтому в каждом конкретном случае необходимо учитывать соотношение параметров Z (кратность связи), σ- и π-связей.
Таким образом целью данного исследования является установление соотношения величины энергии разрыва Э–Э-связей с кратностью (Z) и состоянием гибридизации атомов.
Для С–С-связей нами предложены два уравнения, позволяющие вычислять параметр Z (I)
а) Z = 1 + 25∙(1,540 – ℓ)2 для ℓ ≥ 1,337; (I)
б) Z = 2 + 7∙(1,337 – ℓ)2 + 8∙(1,337 – ℓ)2 для ℓ ≤ 1,337, (I)
где ℓ – длина связи.
Таблица 1
Сравнительные значения энергий диссоциации E (ккал/моль) С–С-, N–N-, О–О- и Р–Р-связей
|
Связь |
σ |
π |
σ + π |
σ + 2π |
2π |
|
С–С |
83 |
63 |
146 |
200 |
117 |
|
N–N |
38 |
66 |
104 |
226 |
188 |
|
О–О |
35 |
83 |
118 |
203 |
168 |
|
Р–Р |
50 |
34 |
84 |
116 |
66 |
Нами также предложен способ учёта изменения гибридизации атомов углерода. На основе имеющихся данных была найдена достаточно простая формула, связывающая долю S-составляющей атома (nS) с кратностью связи (II):
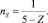(II)
Разность 5 – Z соответствует сумме n + 1 в выражении Spn.
5 – Z = n + 1; Z = 4 – n.
Для бензола, например, Z = 1,5; n = 2,5; n + 1 = 3,5; nS = 0,286 и т.д.
Следует отметить, что формула (II) подтверждает представление о химической связи с дробным порядком, высказанное нами ранее. Так, в работе [5] предложено считать, что в сопряженных системах кратность связи (заселенность её электронами) есть дробная величина порядка связи, расчет которой осуществляется обычно методами квантовой химии.
К аналогичному выводу пришел Р. Гиллеспи (R. Gillespie) [2], отметив, что на основании имеющегося материала можно ввести понятие о химической связи с дробным порядком, если её длина является промежуточной между длинами одинарной и двойной или двойной и тройной связями.
Этот подход позволил нам предложить формулу для вычисления энергии разрыва связи атомов, находящихся в любом состоянии гибридизации. За основу были приняты значения энергии диссоциации одинарной С–С-связи этана (Е = 82,87 ккал/моль), этилена (Е = 146,1 ккал/моль), ацетилена (Е = 199,9 ккал/моль), предложенные В.А. Кондратьевым [5]. Следует отметить, что значения подобных величин, приведенные в других источниках [4–6], мало отличаются от принятых нами.
По приведенным данным была составлена система из двух уравнений (III, IV):
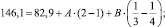(III)
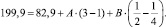(IV)
В результате её решения найдено: А = 72,6 и В = –112,8.
Тогда:
(*)
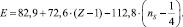Первое слагаемое соответствует энергии σ–связи атомов. Второе отображает вклад в консолидацию молекул за счет π-связей. Вычитаемое –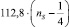 
равно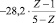 
. Третий член уравнения (ns) учитывает особенности строения атомов (табл. 2)
Подобные соотношения найдены и для других сочетаний атомов. Например, для
N–N – связи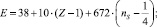 
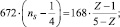
Р–Р – связи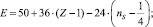 
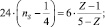
Р–С – связи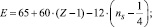 
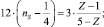
О–О – связи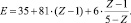 
Таблица 2
Энергия диссоциации углерод-углеродных связей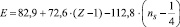 
|
Соединение |
Связь |
ℓ |
Z |
χC |
ns |
Е (ккал/моль) |
|
алканы |
С–С |
1,540 |
1,0 |
2,50 |
0,250 |
82,9 |
|
|
С–С |
1,510 |
1,02 |
2,501 |
0,250 |
84,2 |
|
|
С–С |
1,489 |
1,06 |
2,52 |
0,254 |
86,9 |
|
СН2 = СН2 |
С = С |
1,337 |
2,00 |
2,30 |
0,333 |
146,1 |
|
СН2 = СН─С≡СН |
С–С |
1,434 |
1,28 |
2,50 |
0,269 |
101,1 |
|
СН2 = СН─СН = СН2 |
С–С |
1,465 |
1,14 |
2,52 |
0,259 |
92,0 |
|
СН2 = СН─С≡СН |
С = С |
1,345 |
1,95 |
2,30 |
0,259 |
143,1 |
|
графит |
С…С |
1,420 |
1,36 |
2,43 |
0,275 |
106,2 |
|
СН≡СН |
С≡С |
1,212 |
3,00 |
2,20 |
0,5 |
199,9 |
|
СН≡С–С≡СН |
С–С |
1,384 |
1,61 |
2,37 |
0,295 |
122,1 |
|
СН≡С–С≡СН |
С≡С |
1,218 |
2,94 |
2,20 |
0,485 |
197,2 |
|
СН2 = С = СН2 |
С = С |
1,312 |
2,18 |
2,37 |
0,355 |
156,8 |
|
|
С = С |
1,304 |
2,24 |
2,26 |
0,362 |
160,2 |
|
|
a С…С |
1,359 |
1,82 |
2,33 |
0,314 |
135,2 |
|
b С…С |
1,383 |
1,62 |
2,37 |
0,296 |
122,7 |
|
|
c С…С |
1,412 |
1,41 |
2,41 |
0,279 |
109,5 |
|
|
d С…С |
1,449 |
1,21 |
2,50 |
0,264 |
96,6 |
|
|
|
a С…С |
1,412 |
1,40 |
2,42 |
0,278 |
109,9 |
|
b С…С |
1,371 |
1,70 |
2,35 |
0,303 |
127,9 |
|
|
c С…С |
1,422 |
1,35 |
2,43 |
0,273 |
105,4 |
|
|
d С…С |
1,404 |
1,45 |
2,41 |
0,282 |
111,5 |
|
|
b НС≡С─С≡С─С≡СН |
b С≡С |
1,222 |
2,91 |
2,20 |
0,478 |
194,0 |
|
|
С≡С |
1,232 |
2,82 |
2,20 |
0,459 |
191,5 |
Пример. Для бензола имеем:
ℓ = 1,399; Z = 1,5;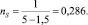 
По формуле (*)
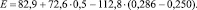
E = 115 ккал/моль.
По [6] E = 116,4 ккал/моль.
С.С. Бацанов [1] показал, что электроотрицательность (χ) атомов в молекуле А–В понижается в зависимости от кратности связи (Z). Известно, что кратность связи в молекуле определяется числом связевых электронов w = 2, 4, 6. С увеличением числа электронов увеличивается число экранирования. Величина экранирования σ зависит также от атомного номера и электронной конфигурации элемента. В общем виде нами показано 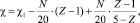(V):
(V)
где χ1 – ЭО элемента при Z = 1, N – атомный номер элемента,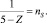 
.
Частное уравнение для углерод-углеродных связей имеет вид (VI):
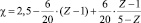
или
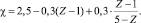(VI)
Для углеводородов, Z которых ≤ 1,31 (N = 6), электроотрицательность принимается равной 2,50. Вычисленные значения χ для графита, бензола, этилена, аллена и ацетилена равны соответственно 2,43; 2,40; 2,30; 2,27; 2,20.
Значения Z, как сказано выше, вычисляются по уравнениям:
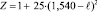для ℓ ≥ 1,337
и
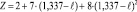для ℓ ≤ 1,337.
Наиболее приемлемый способ вычисления энергии диссоциации галогенов основан на данных констант Тафта σ* и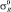 
.
Так, нами предложено уравнение
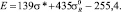
Данные значений σ* и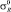 
для галогенов взяты из работы [3], а также вычислены по уравнениям [5]
σ* = 3,84 – r;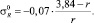 
Для F, Cl, Br, J и At σ* константы соответственно равны 3,20; 2,85; 2,70; 2,50 и 2,40.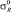 
: –0,35; –0,20; –0,17; –0,13 и –0,11.
Вычисленные значения Е соответственно равны 37,2; 53,8; 45,9; 35,5 и 30,4 ккал/моль.
Выводы
1. Установлено соотношение величины энергии разрыва Э–Э-связей с кратностью связи Z и состоянием гибридизации атомов.
2. Предложена формула для вычисления энергии разрыва С–С-, N–N-, О–О-, и Р–Р-связей атомов, находящихся в любом состоянии гибридизации.