Тепло- и массообменные процессы сушки в барабанных сушильных агрегатах широко представлены в различных производствах химической, нефтехимической, металлургической, легкой и пищевой промышленности Казахстана и стран СНГ. Они используются в качестве основного технологического оборудования для проведения процессов сушки сыпучих и дисперсных материалов. Широкий спектр областей применения тепло- и массообменных аппаратов показывает их доминирующую роль в вышеперечисленных отраслях промышленности, т.е. они определяют технико-экономические показатели производств.
Анализ показывает, что среди всего многообразия конструкций сушильных установок широкое распространение (более 80 %) получили барабанные сушильные агрегаты. Такую популярность они имеют благодаря надежности в работе, простоте конструкции и эксплуатации. Барабанные сушилки универсальны, поскольку позволяют подвергать термообработке широкий спектр материалов, отличающихся как физическими свойствами, так и дисперсным составом (галит, измельченная древесина, семена подсолнечника, семена хлопчатника, хлопок-сырец и др.). Они позволяют достичь равномерной влажности готового продукта и имеют высокую производительность при небольших рабочих объемах.
Сушка является одной из важнейших операций, определяющих не только качество готовой продукции, но и технико-экономические показатели производства в целом.
Так как процесс сушки является весьма энергоемким, то разработка высокоэффективных сушилок указанного типа и методов повышения их эффективности имеет важное экономическое значение.
Анализ литературных и патентных данных показывает, что на сегодняшний день при проектировании барабанных сушилок используются устаревшие данные и методы расчета. К тому же, на протяжении многих лет комплексных исследований, направленных на интенсификацию процессов тепло- и массообмена в них, практически не проводились, а результаты немногочисленных проведенных работ можно использовать только для решения узких задач, т.к. они связаны либо с конкретным материалом, либо с определенной конструкцией сушилки.
Однако в настоящее время отсутствует научно обоснованная методика расчета тепло- и массообменного процесса сушки, учитывающая особенности начального и конечного диаметра, плотности и влагосодержания материала.
Таким образом, разработка тепло- и массообменного процесса сушки в сушильных барабанах, учитывающая его начальный и конечный диаметр, плотность и влагосодержание материала, является актуальной задачей.
В процессе сушки сыпучих и дисперсных материалов в барабанных сушильных агрегатах с наклоном в сторону загрузки в качестве критерия оптимальности выбрана производительность по сухому продукту (1)–(4) [1]:
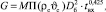 (1)
(1)
где
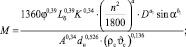 (2)
(2)
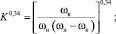 (3)
(3)
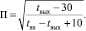 (4)
(4)
В результате опытно-промышленных испытаний сушильного барабана со смешанным режимом термообработки [2] и математической обработки экспериментальных данных получено кинетическое уравнение процесса сушки дисперсных матералов (галита) в сушильном барабане со смешанным режимом термообработки [3]:
 (5)
(5)
В формулах (1)–(5):
G – производительность сушилки по сухому продукту, кг/ч; М; А – коэффициенты; П – температурный коэффициент; К – коэффициент влажности; tвх – температура агента сушки на входе в барабан, °С; tвых – температура сушильного агента на выходе из барабана, °С; ρcϑc – массовая скорость сушильного агента в барабане, кг/(м2⋅с); ρc – плотность газа (воздуха), кг/м3; ϑc – скорость сушильного агента, м/с; Dб – диаметр барабана, м; j – коэффициент заполнения барабана, %; Lб – длина барабана, м; ωн и ωк – начальная и конечная влажность материала, %; n – частота вращения барабана, об/мин; a – угол наклона барабана, град; dн – начальный средний эквивалентный диаметр частицы (определяется по фракционному составу при просеивании), м.
Коэффициент заполнения барабана – j определяем по формуле (6) [3]:
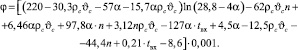 (6)
(6)
Однако вышеуказанное уравнение (5) не учитывает изменения диаметра, плотности и влагосодержания материала в процессе сушки.
Плотность частиц дисперсного материала определяется массой в единице объема частицы [4]:
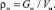 (7)
(7)
Плотность твердой фазы в материале (скелета тела) определяется отношением массы сухого вещества (твердой фазы) к объему, занимаемому сухим веществом [4]:
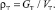 (8)
(8)
Плотность ρТ называют также плотностью скелета тела, а иногда – истинной плотностью.
Важными характеристиками состояния дисперсных систем является относительная пористость частиц eм и пористость неподвижного слоя e0. С помощью этих параметров можно установить связь между плотностями дисперсных систем.
Таким образом, критическую плотность материала [4]
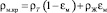 (9)
(9)
можно рассчитывать по плотностям твердой и жидкой фаз, пользуясь принципом аддитивности.
В момент образования агломерата составляющие частички стремятся к максимально плотной упаковке, что обусловлено стремлением системы к уменьшению свободной энергии [5]. При правильной гексагональной укладке сферических монодисперсных частичек в агломерате относительная пористость (eм) достигает 0,2595 [4]. Для полидисперсных сферических частичек относительная пористость eм может достигать 0,15–0,2, для частичек неправильной формы относительная пористость eм ≈ 0,4 [4].
При изменении состояния частицы от суспензии (капли) до агломерата (твердой частицы) размер ее изменяется в соответствии с плотностью и влагосодержанием (влажностью). При этом конечный размер частицы (dк) ограничен критическим влагосодержанием (Cкр). Если частицы суспензии способны деформироваться, то плотность и размер агломератов будут изменяться и после достижения критической влажности. Иногда аномальные изменения наблюдаются и на более ранних стадиях. Например, при сушке некоторых коллоидных растворов и латексов плотность вторичных образований уменьшается, а размеры увеличиваются. Это может быть следствием внутреннего парообразования и формирования полых структур [5].
Конечное значение плотности материала (ρк) при известной начальной плотности (ρн) определяется выражением (10) [4]:
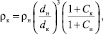 (10)
(10)
где ρн – начальная плотность материала, кг/м3; ρк – конечная плотность материала, кг/м3; dн – начальный диаметр частицы, м; dк – конечный диаметр частицы после сушки, м; Сн – начальное влагосодержание материала; Ск – конечное влагосодержание материала.
Преобразуем выражение (10) относительно начального диаметра частицы dн:
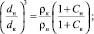 (11)
(11)
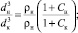 (12)
(12)
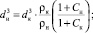 (13)
(13)
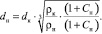 (14)
(14)
Если влажность материала (ω) задана в процентах от общей его массы, то начальное и конечное влагосодержание целесообразно пересчитать по формулам (15), (16) [4]:
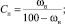 (15)
(15)
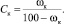 (16)
(16)
Выразив начальное и конечное влагосодержание Сн и Ск через начальную и конечную влажности ωн и ωк согласно выражениям (15), (16), получим
 (17)
(17)
В результате преобразования кинетического уравнения (5), т.е. поставив значение начального диаметра dн (17) и математической обработки с помощью персонального компьютера (ПК) и применения новых инновационных технологий согласно разработанной блок-схеме (рисунок), получено универсальное кинетическое уравнение процесса сушки сыпучих и дисперсных материалов в сушильном барабане со смешанным режимом термообработки (18), учитывающее начальный и конечный диаметр, плотность и влагосодержание высушиваемого материала:
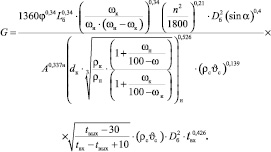 (18)
(18)
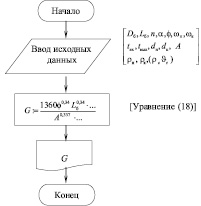
Блок-схема алгоритма расчета процесса сушки сыпучих и дисперсных материалов в сушильном барабане со смешанным режимом термообработки
Уравнение (18) справедливо только для сушильных барабанов, установленных с наклоном в сторону загрузки.
В результате математического моделирования и анализа исследований опытно-промышленных испытаний получено кинетическое уравнение процесса сушки сыпучих и дисперсных материалов в сушильном барабане со смешанным режимом термообработки, учитывающее начальный и конечный диаметры, плотность и влагосодержание высушиваемого материала.



