Модульное обучение ‒ одна из применимых технологий в высших учебных заведениях. Она позволяет порционно давать изучаемый материал с учетом индивидуальных особенностей обучаемых. В данной работе нам хотелось бы показать, что эффективность организации модульного обучения будет выше благодаря использованию информационно-коммуникационных технологий. Применительно к курсу математики в техническом вузе нами был разработан электронный учебник, реализующий структуру модуля по теме «Аналитическая геометрия». С данным средством выполняется работа студентов 1 курса в рамках изучения предмета «Математика».
Рис. 1. Разработка электронного учебника
Данный электронный учебник был разработан в программе «AuthorWare», использует все встроенные механизмы системы: работу с меню, ссылками, встроенную систему тестирования.
Разработанный электронный учебник содержит следующие составляющие.
1. Цели и задачи модуля.
Рис. 2. Работа программного средства «Аналитическая геометрия»
2. Структура модуля, по которой будут работать студенты.
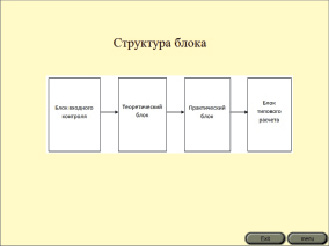
Рис. 3. Вид программного средства со структурой модуля
3. Содержание теоретического, практического блока и блока с типовым расчетом.
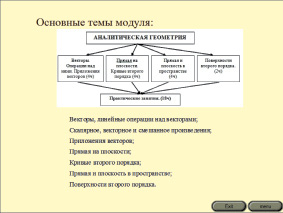
Рис. 4. Содержание программного средства для различных блоков
4. Блок входного контроля содержит тест для повторения соответствующего материала школьного курса планиметрии и стереометрии.
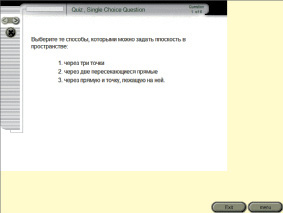
Рис. 5. Вид входного теста, содержащегося в программном средстве
Результаты теста сохраняются в текстовом файле и потом могут быть просмотрены преподавателем.
Блок входного контроля в модуле «Аналитическая геометрия» реализуется через повторение соответствующего материала школьного курса планиметрии и стереометрии, вводную проверку знания определений основных понятий, формул и теорем с целью диагностики уровня сформированности системы знаний, необходимых для изучения данного модуля.
Теоретический блок краткого изложения содержит в себе перечень основных тем модуля, наглядно представленных обучающимся в виде структурных схем. Выделим основные темы модуля «Аналитическая геометрия»:
Векторы, линейные операции над векторами;
Скалярное, векторное и смешанное произведения;
Приложения векторов;
Прямая на плоскости;
Кривые второго порядка;
Прямая и плоскость в пространстве;
Поверхности второго порядка.
Практический блок модуля «Аналитическая геометрия» содержит следующие задачи, описанные ранее:
1. Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс. В декартовой прямоугольной системе координат даны точки М(0; 5), N(–3; 0), K(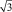
; 1), P(
; 
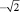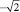), O(1; 
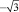). Определить полярные координаты этих точек.
На заключительном этапе изучения данного модуля мы должны оценить полученные студентами знания, для этого в блоке выходного контроля реализуем контролирующий механизм, который выполняет диагностирующие функции. В модуле «Аналитическая геометрия» осуществляется текущий контроль в виде самостоятельных работ по каждой теме и итоговый – в виде типового расчета по всем темам модуля. После итогового контроля происходит анализ и подведение итогов достижения целей обучения, коррекция, определение перспективы дальнейшей работы.
Рис. 6. Вид практического блока учебника
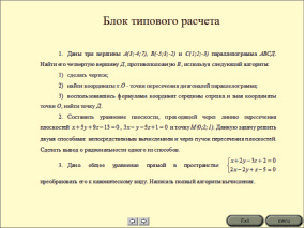
Рис. 7. Вид блока типового расчёта
Представим итоговый типовой расчет по рассматриваемому модулю:
1. Даны три вершины А(3; –4; 7), В(–5; 3; –2) и С(1; 2; –3) параллелограмма АВСД. Найти его четвертую вершину Д, противоположную В, используя следующий алгоритм:
1) сделать чертеж;
2) найти координаты т. О – точки пересечения диагоналей параллелограмма;
3) воспользовавшись формулами координат середины отрезка.
Таким образом, использование модульного обучения в совокупности с применением ИОР при изучении курса математики позволило бы решить часть проблем, встающих перед первокурсниками. К примеру, огромный объём математической информации можно компактно представить в форме модулей, наличием которых решается и проблема отсутствия учебников и задачников. Проблему большой численности студентов на занятиях можно преодолеть обеспечив обучаемых индивидуальными программами и модулями и предоставив им возможность работать независимо от других, самостоятельно организовывая свою учебную деятельность в соответствии не только с требованиями программы, но и со своими способностями и потребностями. Разницу в уровнях базовой подготовки преодолеть путём проработки квалифицированно разработанного модуля, преемственности и разработки системы разноуровневых задач и упражнений.