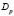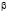Изучение гидродинамики и значение гидродинамической теории смазки для современного производства актуально, так как она дает возможность рационального проектирования и использования подшипников качения, которые в данное время широко используются в различных механизмах и агрегатах.
Первые попытки по развитию и изучению методик по определению теории контактно-гидродинамики были сформулированы в 1883 – 1886 гг. профессором Н.П. Петровым. В то время явления движения вязких жидкостей были мало исследованы, так как работы Осборна Рейнольдса, которые разъяснили сущность ламинарного и турбулентного режимов течения жидкости, были тогда еще мало известны, а следовательно, не было известно, когда возможно, применение уравнений движения вязкой жидкости Навье – Стокса. Ввиду этого Н.П. Петров посвятил значительную часть своей работы доказательству самой возможности применения упомянутых уравнений к вопросу о движении жидкости.
Одним из таких уравнений является определение параметра контактной гидродинамики ε [11], который по В.П. Петрову рассчитывается по зависимости
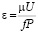 , (1)
, (1)
где μ – динамическая вязкость смазочной жидкости, Па⋅с; U – скорость, м/c; f – коэффициент трения; P – давление на единицу поверхности, Па.
В зависимости В.П. Петрова степени скорости U коэффициента трения f, давления на единицу поверхности P равны единице, а пьезокоэффициент вязкости и коэффициент изменения толщины масляной пленки не учитывались.
Существует ещё несколько общеизвестных положений [4, 5] для определения толщины масляной пленки, рассмотренные в работах Эртеля – Грубина, Хиггинсона, Хэмрок-Джекобсон, Доусона, Ратнера, где учтены вышеуказанные параметры и коэффициенты. На основании обобщения их работ предложена зависимость толщины масляной пленки, выраженная в безразмерных параметрах:
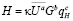 , (2)
, (2)
где k – константа, включающая модуль упругости; U – суммарная скорость качения; a – коэффициент, характеризующий суммарную скорость качения; G – приведенный радиус кривизны поверхностей; b – коэффициент, характеризующий радиусы кривизны поверхностей; 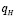 – эквивалентная статическая нагрузка на единицу длины контакта; с – коэффициент, характеризующий параметр нагрузки.
– эквивалентная статическая нагрузка на единицу длины контакта; с – коэффициент, характеризующий параметр нагрузки.
На рис. 1 представлен контакт ролика с дорожкой в динамике совместно со смазочным материалом.
При экспериментальных исследованиях данных ученых были получены коэффициенты, представленные в табл. 1.
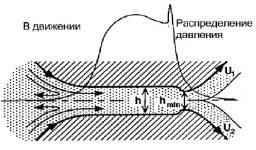
Рис. 1. Контакт ролика с дорожкой в динамике совместно со смазочным материалом
Таблица 1
Коэффициенты показателей для определения толщины масляной пленки при экспериментальных исследованиях
|
Авторы |
K |
a |
b |
c |
|
Эртель – Грубин |
1,95 |
0,727 |
0,727 |
– 0,091 |
|
Хиггинсон |
1,6 |
0,7 |
0,6 |
–0,13 |
|
Хэмрок-Джекобсон |
3,07 |
0,71 |
0,57 |
–0,11 |
|
Доусон |
2,65 |
0,7 |
0,54 |
–0,13 |
|
Ратнер |
3,17 |
0,75 |
0,6 |
–0,15 |
Вследствие того, что рабочие условия редко бывают идеальными и на практике не всегда удается записать в явном виде полную систему уравнений, достаточно точно отражающую свойства объекта, и определить из нее критерии подобия, возникает необходимость использования соотношений сил, действующих в объекте, так называемый метод подобия [2, 12, 15].
При использовании теории подобия и проведении экспериментальных исследований, для определения моментов сопротивления в подшипниках качения применяются различные подходы. Например, при определении коэффициента по толщине пленки смазочного материала 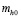 и контактных напряжений
и контактных напряжений 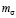 использовалась формула Ратнера (3), с коэффициентом, характеризующим суммарную скорость качения, равным 0,75, коэффициентом, характеризующим радиусы кривизны поверхностей, 0,4 и коэффициентом, характеризующим параметр нагрузки, –0,15:
использовалась формула Ратнера (3), с коэффициентом, характеризующим суммарную скорость качения, равным 0,75, коэффициентом, характеризующим радиусы кривизны поверхностей, 0,4 и коэффициентом, характеризующим параметр нагрузки, –0,15:
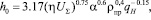 (3)
(3)
где h – динамическая вязкость масла при атмосферном давлении и рабочей температуре, Па∙с; UΣ – суммарная скорость качения на контакте, м/с; α – пьезокоэффициент вязкости, Па-1; ρпр – приведенный радиус кривизны поверхностей трения, м; qн – нагрузка на единицу длины контакта, Н/м.
Для более корректного описания изменения толщины масляной пленки в зависимости от скорости и усилий прокатки на стане 2000 холодной прокатки были проведены лабораторные исследования. Используя экспериментальную установку для моделирования процессов смазки в подшипниковых узлах рабочих и опорных валков, выявлены закономерности.
В соответствии с теорией подобия, используя зависимость (3), заменим все величины через их масштабные коэффициенты:
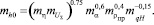 (4)
(4)
При использовании одного и того же смазочного материала на реальных объектах и экспериментальных установках можно определить, что масштабные коэффициенты динамической вязкости при атмосферном давлении и рабочей температуре 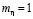 и пьезокоэффициента вязкости
и пьезокоэффициента вязкости 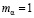 . В связи с принятыми выше допущениями получим зависимость:
. В связи с принятыми выше допущениями получим зависимость:
Тогда зависимость (4) примет вид
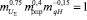 . (5)
. (5)
Технические характеристики подшипников представлены в табл. 2.
Таблица 2
Технические характеристики подшипников
|
Параметры |
Обозначение |
Koyo |
№ 97516 |
|
Величины |
|||
|
Внутренний диаметр, мм |
d |
317 |
80 |
|
Средний диаметр, мм |
D0 |
369,5 |
110 |
|
Диаметр ролика, мм |
|
23 |
14,7 |
|
Длина ролика, мм |
l |
40 |
23,4 |
|
Число тел качения, шт. |
Z |
39 |
19 |
|
Количество рядов роликов, шт. |
i |
4 |
2 |
|
Угол контакта, град |
|
15 |
15 |
Для заданных условий найдём масштабный коэффициент приведенного радиуса кривизны поверхностей трения 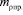 [3, 6, 18]:
[3, 6, 18]:
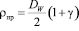 ; (6)
; (6)
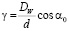 ; (7)
; (7)
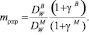 (8)
(8)
Из вышеперечисленных формул определим
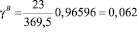 ;
;
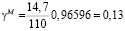 ;
;
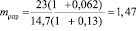 .
.
Для определения масштабного коэффициента нагрузки на единицу длины контакта 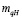 воспользуемся зависимостью [3, 6, 18]:
воспользуемся зависимостью [3, 6, 18]:
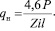 (9)
(9)
Соответственно
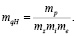 (10)
(10)
Из решения вышеперечисленных зависимостей получаем
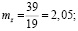
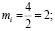
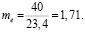
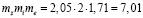 .
.
Нагрузку на подшипник 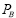 найдём с учётом горизонтальной составляющей давления металла на валки P = 35 МН и усилия противоизгиба Pпр = 500 кН [14]:
найдём с учётом горизонтальной составляющей давления металла на валки P = 35 МН и усилия противоизгиба Pпр = 500 кН [14]:
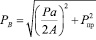 , (11)
, (11)
где P – давление металла на валки, Н; a – величина смещения оси рабочего валка относительно оси опорного валка, м; А – межосевое расстояние, Pпр – усилие противоизгиба, Н;
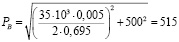 (кН).
(кН).
Нагрузка на подшипник ЭУ задаётся равной 6 кН, тогда
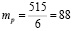 , а
, а 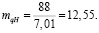
Используя зависимость (5), определим значение масштабного коэффициента суммарной скорости качения 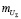 :
:
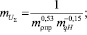 (12)
(12)
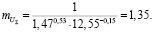
Взаимосвязь между суммарной скоростью качения 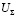 и числом оборотов n определяется зависимостью [5]
и числом оборотов n определяется зависимостью [5]
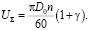 (13)
(13)
Тогда масштабный коэффициент числа оборотов n 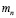 найдём из зависимости
найдём из зависимости
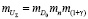 . (14)
. (14)
Для
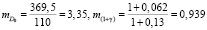
получаем

Тогда частота вращения вала на ЭУ должна быть равна:
Из технологической инструкции [14] частота вращения по всем клетям для стана 2000 холодной прокатки приведена в табл. 3.
Таблица 3
Частота вращения рабочих валков по всем клетям
|
Номер клети |
1 |
2 |
3 |
4 |
5 |
|
nв (рабочих валков), об./мин |
0–345 |
0– 50 |
0–756 |
0–962 |
0–995 |
Таким образом, частота вращения вала на ЭУ должна составлять 1200 об./мин для условий 2-й рабочей клети и 1700 об./мин – для условий 3-й рабочей клети стана. В дальнейшем с использованием приведенных зависимостей была проведена серия лабораторных экспериментов на экспериментальной установке моделирования процессов смазывания в подшипниковых узлах [7], с различными классами вязкости (КВ) смазочного материала (мм/с2), такими как: И 40 с КВ 68, И 100 РС, с КВ 100, Mobil 600 XP 220 с КВ 220, ТНК 460 с КВ 460.
Используя вышеперечисленные зависимости и проведенные лабораторные исследования, разработали программу для ЭВМ в среде Visual Basic по контактно-гидродинамическому расчету подшипников качения для станов холодной прокатки при скорости прокатки до 2000 м/мин и нагрузках до 40 МН. Интерфейс программы с показаниями входных данных представлен на рис. 2, интерфейс программы с сохраненным расчетом в базе данных изображен на рис. 3 [13].
Рис. 2. Интерфейс программы с показаниями входных данных

Рис. 3. Интерфейс программы с сохраненным расчетом в базе данных
Таким образом, учитывая полученные экспериментальные, лабораторные исследования и обобщенные положения при определении толщины масляной пленки, была разработана программа для ЭВМ в среде Visual Basic по контактно-гидродинамическому расчету подшипников качения при выбранных технологических условиях работы стана холодной прокатки, позволяющая выявлять отклонения от заданных параметров и своевременно изменять режимы смазки. В программе имеется возможность сохранения исходных условий и результатов расчета в базе данных, может быть использована как в учебном процессе, так и на практике при решении вопросов продления ресурса подшипников качения.
Модель контактно-гидродинамического расчета подшипников качения, реализованная в программе, актуальна для узлов трения машин бесфильерного волочения проволоки [1, 8, 19, 20], а также для узлов трения алмазно-канатных машин и другого оборудования, задействованного при добыче блочного высокопрочного камня [9, 10, 16, 17].