Пусть X – сепарабельное банахово пространство. Говорят, что последовательность F Х-значных случайных элементов удовлетворяет усиленному закону больших чисел (УЗБЧ), если для любой подпоследовательности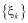 
из F
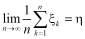п.н.,
где η – некоторый случайный элемент.
В [2] показано, что любая ограниченная по норме в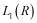 
последовательность скалярных случайных величин содержит подпоследовательность, удовлетворяющую УЗБЧ. Для бесконечномерных Х-значных случайных элементов эта теорема, вообще говоря, не верна. Соответствующий пример построен в [1].
Нами доказано следующее утверждение.
Теорема. Пусть банахово пространство X таково, что из любой равномерно ограниченной в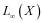 
последовательности случайных элементов можно извлечь подпоследовательность, удовлетворяющую УЗБЧ. Тогда из любой равномерно ограниченной в 
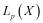, где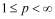 
, последовательности случайных элементов, можно извлечь подпоследовательность, удовлетворяющую УЗБЧ .