Горные породы в условиях естественного залегания способны проявлять упругие и пластические свойства. Это свойство характерное для деформируемых твердых тел проявляется при сооружений горной выработки.
С переходом горнодобычных работ на большие глубины при достаточно высоком уровне статических и динамических (сейсмических) нагрузок горные породы вокруг пустых полостей (выработок) могут переходить в предельное состояние, а величины статических и сейсмических напряжений, превосходить пределы прочности горных пород, приводя к образованию зон неупругих деформаций, охватывающих полностью или частично контур выработки.
Существуют множество модели определения пластических зон в массиве вблизи контура подземного сооружения находящегося в горном массиве изотропного строения. Однако, модель массива как изотропного тела далеко не полностью описывает наблюдаемые в натуре особенности проявления горного давления. Попытка решить задачу в такой постановке для транстропного массива была предпринята в работах Ж.К. Масанова и М.Е. Ескалиева [1-3] на основе применения полу-обратного метода Перлина [4,5] для выработки находящегося в бесконечной среде. Вопрос исследования закономерности возникновения пластических зон вокруг выработки находящегося в тяжелой полуплоскости, материал, который состоит из горной породы, имеющее наклонно-слоистое строение пока еще не изучен. Задача еще более осложниться тем что, если горная выработка находиться в массиве неоднородно анизотропного строения. Прежде чем решить задачу в упругопластической постановке, немаловажно знать закономерности перехода массива вокруг выработки в пластическое состояние в направлениях вдоль и в крест слоев плоскости изотропии, а также в направлениях между ними, т.е. на главных площадках. Неизвестно также, на какой глубине начинается появления пластических зон в тяжелом наклонно-слоистом транстропном массиве вокруг горной выработки в зависимости от воздействия геостатических и тектонических сил. Естественно, такую задачу необходимо решить сначала методом предельного перехода. Для решения задач механики деформируемого твердого тела предельным переходом в качестве условии пластичности часто применяется соотношения Кулона-Мора, которая удобна тем, что позволяет одновременно определить возникновения зон пластичности от растягивающих и сжимающих напряжений.
Условие пластичности Мизеса с экспериментальными данными дает достаточно близкие результаты (энергетическое условие пластичности)
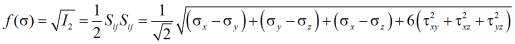(1)
здесь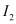 
– второй инвариант девиатора напряжений, 
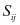– компоненты девиатора напряжений
; 
,
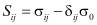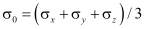где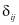 
– символ Кронекера.
Условие Мизеса приблизительно описывает течение изотропного материала. Поэтому простейшим условием текучести для анизотропного материала является то, которое сводится к закону Мизеса, когда анизотропия исчезающее мала.
Для ортотропного тела Хиллом было предложено условие пластичности, которое является обобщением условия Мизеса на анизотропные тела. Если x, y, z являются главными осями анизотропии, условие пластичности Хилла имеет вид
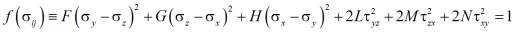2
(2)
где F, G, H, L, M, N – параметры анизотропии. Постоянные в этом условии текучести можно определить, для частных случаев одноосных растяжений в направлениях осей x,y,z и сдвигов между этими осями. Если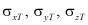 
– пределы текучести при растяжении в главных направлениях анизотропии, тогда
, 
;
, 
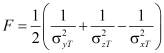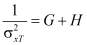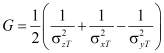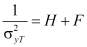; (3)
, 
;
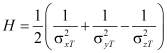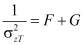Если L,M,N – пределы текучести при сдвиге по отношению к главным осям изотропии, то в этом случае
, 
, 
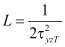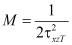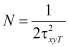. (4)
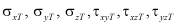– ординаты диаграмм растяжений и сдвигов в различных направлениях.
Для применения условия пластичности Хилла необходимы экспериментальные данные для определения шести параметров F,G,H,L,M,N из выражений (3) и (4) для транстропного горного массива. Этими вопросами также занимались зарубежные ученые из Бельгии – В. Хейгеман, К. Пириякул, из Японии – Ф. Татсуоко, Т. Сато и другие, из Ирана – А. Ахмади, А. Галандарзадех и другие. Но все экспериментальные данные в их работах относятся к грунтам и преимущественно для нахождения упругих свойств грунтов анизотропного строения.
Из-за отсутствия экспериментальных данных для горных пород мы поступим следующим образом. Поскольку имеются некоторые экспериментальные предельные данные для горных пород транстропного строения, то применительно к нашей задаче для нахождения пластических зон вдоль и вкрест слоев плоскости изотропии мы можем определить неизвестные параметры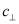 
, 
, 
, 
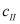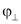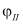используя круги Мора (рис. 1). Смысл этих рисунков сводится к следующим. Из экспериментальных данных снимаются критические значения максимальных 
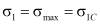и минимальных 
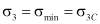и по ним раздельно строятся круги Мора. Значения 
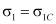наносится на положительное направление оси напряжений, а минимальное напряжение наносится на отрицательное направление со знаком минус: 
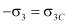. На полученные круги проводим касательные. Точки пересечения по оси t, нам дадут значения сил сцепления вдоль слоев 
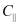(рис. 1а) и перпендикулярно слоям 
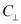(рис. 1б). Измеряем углов внутренних трений вдоль слоев 
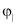и перпендикулярно слоям 
.
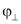Теперь мы можем записать новое обобщенное условие пластичности Кулона-Мора для транстропного массива в следующем виде
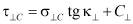(5)
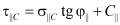(6)
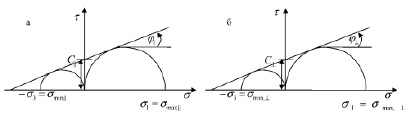
Рис. 1. Построение кругов напряжений Мора для нахождения значений критических сил сцеплений и внутренних трений вдоль (а) и вкрест (б) слоев плоскости изотропии –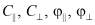 
.
После нахождения по МКЭ значений напряжений в элементах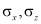 
и 
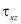значений главных напряжений и направлений главных площадок a – вычисляем с помощью следующих известных выражений теории упругости
,
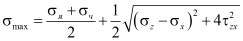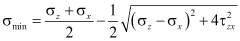, (7)
,
.
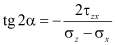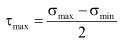Кроме максимальных и минимальных компонент напряжений Значений нормальных компонент напряжений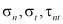 
вкрест и вдоль слоев плоскостей изотропии, вычисляем с помощью следующих соотношений, после применения формул преобразования
,
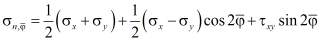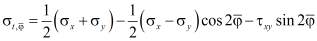, (8)
.
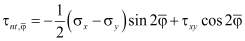Но, направления главных площадок α вычисляемый из (7), может не всегда совпадает с углом плоскости изотропии ϕ. Поэтому нормальных компонент напряжений на главных площадках вычисляется с помощью угла α следующими выражениями
,
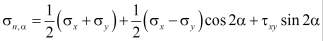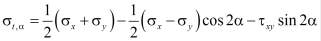, (9)
.
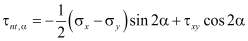Смысл сказанного раскрывает рис. 2.
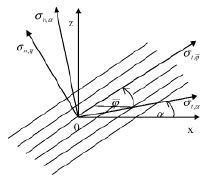
Рис. 2. Ориентации главных площадок α главных напряжений и угла наклона плоскости изотропии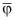 
относительно горизонтальной оси Ox декартовой системы координат xOz
Теперь можно сформулировать условий возникновения неупругих зон в направлениях вдоль и вкрест слоев плоскости изотропии наклоннослоистого транстропного массива.
Если максимальное значение касательных напряжений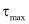 
вычисляемый по выражению (7) из МКЭ:
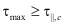(10)
то пластическая зона развивается вдоль слоев плоскости изотропии.
Если
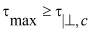(11)
то пластическая зона развивается перпендикулярно слоям плоскости изотропии.
Пластическая зона для заданного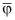 
, может развиваться между направлениями вдоль и вкрест, т.е. в направлений 
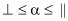, а также главных площадок a. Для этих направлений условию пластичности мы можем записать с помощью выражений типа Казагранде – Коррилло в виде
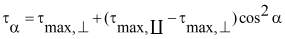, (12)
где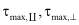 
экспериментально определяемые критические значения горных пород слоистого строения для случаев 
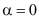и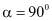 
т.е. вдоль и вкрест слоев плоскости изотропии. Сравнивая вычисленные величины максимальных касательных напряжений 
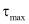по (7) с их критическими величинами по (12) определяется направление и зоны распространения пластичности для любого α.