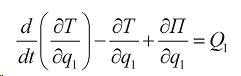
где T-кинетическая энергия агрегата;
Q - обобщенная сила;
T - время;
П - потенциальная энергия системы ;
i= 1.2.3......К -число степеней свободы системы.
Уравнение лагранжа представляет совокупность дифференциальных уравнений с K oобобщенными координатами по числу степеней свободы. Для изучения тяговой динамики агрегата при установившемся движении агрегата будем иметь одно уравнение.
Перемещение и скорость агрегата можно задать угловой скоростью коленчатого вала и связанную с ней поступательной скоростью агрегата
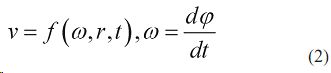
Произведение обобщенной силы на обобщенную координату определяет работу системы. За обобщенную силу Q примем разность - крутящего момента , и момента сопротивления движению агрегата от крюковой и дополнительной тяговой нагрузки,приведенных к валу двигателя

определяет касательную силу тяги трактора; -силу тяги на крюке и другие силы сопротивления движению
Кинетическая энергия мобильного агрегата равна

Ia — момент инерции агрегата, приведенный к валу двигателя упругая связь трактора с комбинированной машиной определяется уравнением потенциальной энергии пружины

где с — коэффициент жесткости упругой связи трактора с комбинированной мащиной
x — величина продольной деформации упругой связи машины с трактором (навески, амортизатора,пружины,тяговых соединений и т.д.)
С учетом полученных уравнений (2–5), общее уравнение динамики для тракторного агрегата имеет вид:
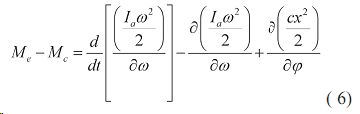
Для представления уравнения (6) в развернутом виде и его решения необходимо знать функциональные зависимости входящих в это уравнение величин. Величина приведенного момента инерции зависит от скорости движения агрегата. В свою очередь на величину скорости влияют буксование движителей — δ, деформация упругой связи — δy, буксование муфты сцепления — δm, потери жидкости в гидростатической передаче — δr.
Каждый из этих коэффициентов определяется отношением скоростей
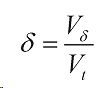
Vt — рассчетная скорость агрегата;
Vδ — действительная скорость агрегата.
С учетом всех коэффициентов снижения скорости, действительная скорость движения определяется зависимостью
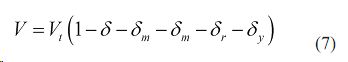
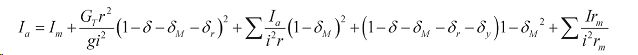
Приведенный момент инерции будет равен
Im-момент инерции маховика и приведенных к нему масс двигателя;
i — передаточное число трансмиссии трактора ;
GT — полный вес трактора;
Ir — момент инерции любой вращающейся детали;
irM -передаточное число от вала двигателя к любой детали IrM -момент инерции любой вращающейся детали при вращении от вала отбора мощности;
ir — число от двигателя к любой детали;
Ga = Gm + GТ полный вес комбинированного агрегата.
rк — радиус ведущих колес трактора;
Gm — полный вес комбинированной ма- шины.
При выключенной муфте сцепления или полном буксовании δm=1, а все члены уравнения ( 8) равны нулю .Тогда Ia=Im .
Для тракторов с механической трансмиссией δr=0
После трогания комбинированного агрегата влияние упругих деформаций связей незначительно, поэтому разность можно заменить — определяющей к.п.д. учитывающего потери на буксование мобильного агрегата. Тогда приведенный момент инерции будет равен:
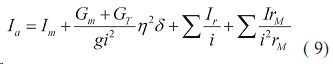
Ограничимся анализом влияния на приведенный момент инерции и на динамику трактора двух наиболее важных факторов — переменного передаточного отношения трансмиссии и к.п.д. буксования, включая в это понятие учет потерь скорости под действием факторов ,определяемых уравнением (7).При указанных условиях уравнение (6) приводится к виду:
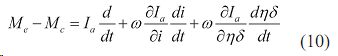
При постоянных передаточных числах трансмиссии и буксовании, уравнение упрощается
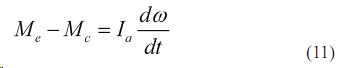
Задача максимального динамического нагружения на механизмы трансмиссии решалась В.Н. Болтинским. Для оценки влияния трансмиссии и буксования на снижение динамических нагрузок найдем частные производные уравнения (9) и сделаем преобразования:
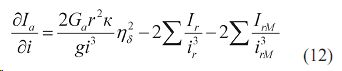
Производную передаточного числа трансмиссии заменим равенством:
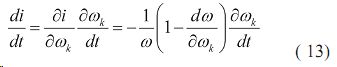
Для последнего члена правой части уравнения (10) справедливо:
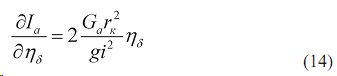
При ηδ=1-δ dηδ=-dδ в пределах линейной зависимости буксования от силы тяги на крюке справедливо равенство δ=mPкр и dδ=mdPкр, где m — постоянный коэффициент интенсивности буксования. С учетом записи
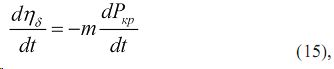
уравнения (10) и зависимостей (12,12,13,14, 15) получим :
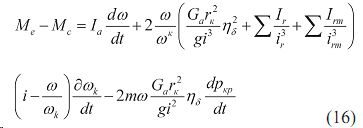
Для трактора со ступенчатой трансмиссией ω/ ωk=1 средний член равенства (16) обращается в нуль, а уравнение имеет вид:
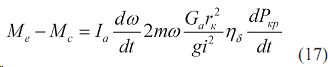
При непрозрачной трансмиссии =0 остаточный крутящий момент равен:
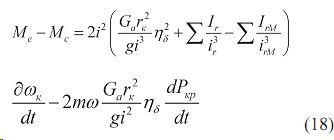
С увеличением скорости движения при уменьшении передаточного числа и при наличии бесступенчатой трансмиссии снижаются динамические нагрузки. При увеличении приведенного момента инерции повышается устойчивость и равномерность движения агрегата ,поскольку растет обобщенная сила системы.
Приведенный момент инерции существенно влияет как на колебания комбинированного агрегата относительно линии тяги трактора, так и на агротехнические погрешности, возникающие при отклонениях от прямолинейного хода рабочих органов.
Исходя из уравнения лагранжа применительно к перемещению комбинированной машины в параметрах динамической схемы нагружения, получим конечные уравнения, описывающие поведение динамической системы
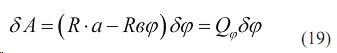
Приравнивая значения обобщенной силы, имеем:
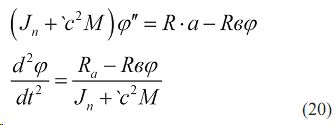
Это дифференциальное уравнение является математической моделью движения комбинированного агрегата.
Где а — расстояние от центра давления до главной оси инерции агрегата ;
в — расстояние от равнодействующей центра давления до центра тяжести агрегата;
´с – плечо момента устойчивости (от центра тяжести до точки прицепа агрегата).
Разделим правую часть на коэффициент при, и сделав замены :
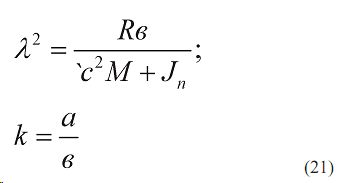
Получим дифференциальное уравнение колебаний комбинированного агрегата относительно точки прицепа:
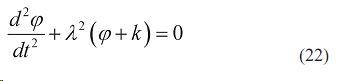
![]()
Произвольные постоянные C1,C2 определяют:
При t=0, φ=0, φ´=0, C1=–k,C2=0
Опуская промежуточные вычисления, уравнение можно привести к виду:
φ=k(1–cosλt) (23)
Заменяя k и λ их значениями, получим геометрические и динамические соотношения параметров комбинированного агрегата.
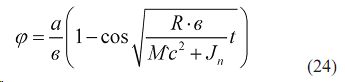
Амплитуда колебаний от внешних сил и изменения параметров системы смещается в сторону увеличения угла φ. Уравнение (24) показывает, что с увеличением асимметрии внешней нагрузки и с увеличением смещения от оси вращения, угол φ возрастает. С другой стороны при увеличении c´ угол φ уменьшается. При увеличении веса и момента инерции рыхлителя, колебания системы становятся более плавными, а их амплитуда уменьшается обратно пропорционально корню квадратному из величин роста момента инерции устройства. При проектировании рабочего органа необходимо уменьшать k, увеличивая значения в.
k →kmun=a/в
Для стабилизации плавности хода агрегата необходимо увеличивать его продольный размер .
Смещение центра тяжести равно
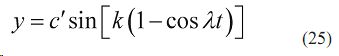
или
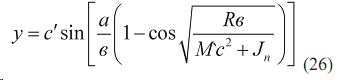
Уравнение (26) можно представить в виде одночлена удобного для операционных вычислений по уравнению
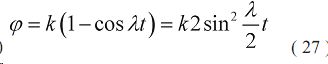
Для этого значения подставляем в уравнение :
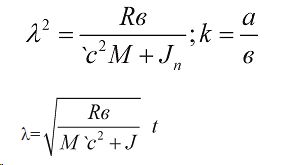
В итоге получим закономерность влияния только момента инерции агрегата на изменения угла λ отклонения от положения равновесия. Для этого примем значение k

Установлено, что при увеличении ширины захвата возрастает момент инерции агрегата .При этом одновременно стабилизируется плавность хода и возрастает его производительность.
Заключение
Полученные уравнения тяговой динамики в дифференциальной форме позволяют выявить и оценить факторы, влияющие на динамическую напряженность трактора и комбинированной машины. При увеличении момента инерции агрегата уменьшаются его угловые и линейные колебания , а динамическая система при этом работает более устойчиво.



