где F1,F2,F3 - функционалы, X(t) - выходной сигнал, Y(t) - входной сигнал, t - время.
Рассмотрим указанные функционалы в виде (например, для X(t)):
X(t) = B0 + B1*Ex(t) + B2 *G(t) + B3 *F(t) + B4* ε(t), (2)
где Bi - параметры уравнения, Ex(t), G(t), F(t), ε(t) - соответственно: экспоненциальная, гармоническая (колебательная), алгебраическая и случайная составляющие (термы).
В условиях маломощности экспериментального материала (несколько десятков регистраций) для идентификации (2) предлагается следующий метод, основанный на синтезе статистического и самоорганизационного подходов.
- Регистрируется вектор значений {Xt /t=1,...n} и приводится к единичному диапазону {X*t}.
- Увеличивается мощность {X*t}, путем уменьшения кванта времени, применяя интерполяционный многочлен, до нескольких сотен дискрет. (Применять в данном случае «раскачку Шеннона» не рекомендуется, поскольку появляется реально не существующая случайная составляющая).
- Формируются обучающая {X*t}о и экзаменационная {X*t}э выборки по следующей методике с обязательным включением в той же пропорции реальных (не интерполированных) значений {X*t}. Для достижения условия подчинения указанных выборок одному закону распределения предлагается поступать следующим образом. Характеризующий объект вектор зарегистрированных показателей сворачивается в одно значение, например, нормируя по дисперсии, как предлагает академик Ивахненко А.Г. :
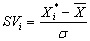, где SVi - свертка характеристик объекта,
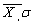- соответственно средняя величина и СКО. По датчику случайных чисел равномерного закона распределения формируется обучающая выборка из упорядоченных соответственно значениям номеров измерений требуемой мощности. Оставшиеся объекты формируют экзаменационную выборку. Соотношения объемов обучающей и экзаменационной выборок рекомендуется придерживаться принципа «золотого сечения» - 0,62:0,38. - Идентифицируются на обучающей выборке методом наименьших квадратов параметры формулы (2), рассчитывая для каждого из вариантов (см. Таблицу 1) СКО отличий аппроксимантов от значений Х* на экзаменационной выборке.
- В качестве итоговой математической модели (2) выбираются l лучших вариантов полученных в п.5 и осуществляется переход к реальным значениям Х и масштабу времени с учетом выполненных операций в пп.2 и 3. Свобода выбора решений l определяется исследователем или, в общем смысле, системой управления.
Таблица 1. Варианты структур формулы (2)
|
№ варианта |
Порядок включения составляющих термов в процессе идентификации (2) |
Характеристики модели |
|||||||
|
Ex(t) |
G(t) |
F(t) |
ε(t) |
B0 |
B1 |
B2 |
B3 |
СКО |
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 .... 56 |
1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 3 3 ... 0 |
2 3 3 4 0 0 2 3 2 3 2 0 0 0 1 1 1 ... 0 |
3 2 4 3 2 3 3 2 0 0 0 2 0 0 3 2 4 ... 0 |
4 4 2 2 3 2 0 0 3 2 0 0 2 0 4 4 2 ... 1 |
|
|
|
|
|
Таким образом, исследователь имеет l наиболее адекватных в статистическом смысле решений уравнений динамики.
При расчете параметров В рекомендуется применять процедуру «выметания» статистически незначимых термов, например, по критерию Стьюдента.
Составляющие формулы (2) предлагается идентифицировать следующими способами:
- Для Ex(t) - из набора: A0*EXP(A1 t), EXP(A0+A1*t), A0+A1*CH(t), A0+A1*SH(t), A0+A1*TH(t), A0+A1*ACH(t), A0+A1*ASH(t), A0+A1*ATH(t);
- Для G(t) - применяется аппарат метода группового учета аргументов синтеза математических моделей по некратным гармоникам (или применить Фурье-анализ с последующим отбросом незначимых термов);
- Для F(t) - из набора: А0 + А1*t, А0 + А1*Ln(t), 1/(А0 + А1*t), А0/(А1+t), А0*t/(A0+А1*t), t /(А0+А1*t), А0*А1t, А0*А1-t, А0+А1/t , А0+А1*t+A2*t2;
- Для ε(t) - по методике, предложенной И.Г.Уразбахтиным.
Таким образом, селекция лучших математических структур (2) на рядах самоорганизационного моделирования позволяет получить наиболее адекватное решение поставленной задачи.