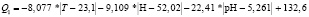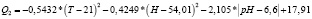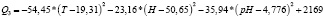Введение
В условиях растущей урбанизации и высокой плотности населения крупных мегаполисов вертикальное земледелие становится все более актуальным и востребованным методом выращивания сельскохозяйственных культур [1]. Этот метод позволяет значительно увеличить урожайность на единицу площади, что делает его идеальным решением для обеспечения продовольствием в условиях плотной городской застройки.
В условиях, когда ресурсы ограничены, а население продолжает расти, вертикальное земледелие становится ключевым элементом устойчивого развития. Оно не только обеспечивает продовольственную безопасность, но и способствует созданию новых рабочих мест и развитию инновационных технологий.
В данной статье рассматривается совершенно новый метод вертикального земледелия – аэроаквапоника. По своей сути и особенностям это результат слияния технологии аквакультуры и аэропоники [2], то есть растения выращиваются так же в условиях аэропоники, но питательный раствор берется в результате жизнедеятельности рыб, что является аналогом технологии аквапоники [3], которая так же основана на аквакультуре, только в условиях гидропоники.
Главным преимуществом новой технологии и ее превосходством над аквапоникой является полная универсальность. В данных условиях возможно выращивать абсолютно любые растения и разводить любые породы рыб, так как непосредственного контакта биологических видов, как в аквапонике, не происходит.
Аэроаквапоника открывает новые горизонты для сельского хозяйства, позволяя эффективно использовать ограниченные ресурсы и создавать устойчивые системы производства продовольствия. Этот метод не только способствует улучшению экологической ситуации, но и предоставляет возможности для экономического роста и социального развития. Аэроаквапоника представляет собой перспективное направление в области вертикального земледелия, которое может стать важным элементом устойчивого развития городов и обеспечения продовольственной безопасности в будущем.
Цель работы – получение адекватной математической модели технологического процесса аэроаквапоники.
Материалы и методы исследования
Для получения наибольшего урожая необходимо выдерживать все параметры технологического процесса на заданном уровне.
Таким образом:
Q = f (T,H,D,Λ,S,C,A,r,N,V,pH) → max, (1)
где Q – количество произведенной продукции за единицу времени, кг/ед. времени;
Т – температура, оС;
H – относительная влажность, %;
D – цикл освещенности, ч;
Λ – интенсивность, мкмоль/м2*с;
S – цикл распыления раствора, мин;
C – состав, мг;
A – аэрация корней, мин;
r – расстояние между растениями, м;
N – сорт картофеля;
V – порода рыбы;
pH – значение параметра рН жидкости.
В результате проведенного анализа отметим, что из всех ранее обозначенных переменных, входящих в выражение критерия оптимальности (1), были найдены и выведены все фиксированные значения переменных, кроме температуры, влажности и pH раствора.
В результате критерий оптимизации (1) для выращивания картофеля в аэроаквапонной установке сводится к следующему виду:
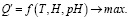(2)
Задача максимального прироста картофеля, производимого за технологический цикл, описанная ранее в формуле (2), является довольно общей, и поэтому для ее решения необходимо наложить некоторые ограничения, обоснованные физической сущностью процесса. Конечный вид функции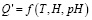 
не известен. Это можно объяснить как сложностью и весьма малой математической формализацией процесса выращивания картофеля в условиях вертикального земледелия, так и выращивания картофеля в условиях аэроаквапоники в частности.
В связи с вышесказанным было принято решение воспользоваться экспериментальным методом определения экстремальных характеристик. При этом на основании [4–6] и исследованиях [7] на аргументы функции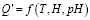 
накладываются следующие ограничения:
- Т ≥ 18ºС;
- Т ≤ 24ºС;
- Н ≥ 50%;
- Н ≤ 55%;
- рН ≥ 6,5;
- рН ≤ 8.
Однако, учитывая, что при росте и развитии куста картофеля растение проходит три фазы развития, предполагается, что необходимо произвести несколько экспериментов, непосредственно связанных с результатом предыдущей фазы, как продолжение максимального прироста.
Инструментом для получения экспериментальных данных для функции Q' = f (T,H,pH) является эксперимент.
Для первой фазы:
− берется 100 здоровых картофелин среднего размера по 100–150 г каждая и помещается в аэроаквапонную установку;
− производится сбрызгивание картофеля питательным раствором с заранее заданным интервалом в зависимости от фазы роста с одновременным контролем уровня влажности;
− производится увеличение значения pH с одновременным контролем значения параметра;
− все действия производятся при необходимой температуре и уровне аэрации;
− эксперимент прекращается при прорастании как минимум 70 % картофелин;
− если более 30 % картофелин погибло, эксперимент считается неудачным, комбинация значений не подходит под заданные значения оптимальности;
− при прекращении эксперимента вычисляется общее количество проросших картофелин (учитываются только здоровые корнеплоды с хорошо развитой корневой системой) и время, которое было затрачено на произрастание картофеля.
Для второй фазы:
− картофель из наилучшего по времени и качеству эксперимента переходит во вторую фазу эксперимента (при необходимости для второй фазы дополнительно проращивается картофель по уже известным параметрам первой фазы);
− производится сбрызгивание картофеля питательным раствором с заранее заданным интервалом в зависимости от фазы роста с одновременным контролем уровня влажности;
− производится увеличение значения pH с одновременным контролем значения рН;
− все действия производятся при необходимой температуре и уровне аэрации;
− эксперимент прекращается при образовании почек на корнях как минимум 70 % кустов картофеля.
− если более 30 % картофелин погибло, то эксперимент считается неудачным;
− при прекращении эксперимента во второй его фазе производится оценка размеров куста и количества клубней картофеля.
Для третьей фазы:
− в последней фазе эксперимента производится выращивание кустов картофеля с наибольшим размером вегетативной части и при этом наибольшим числом почек. Растения, полностью ушедшие в вегетативную часть, также отбраковываются и считаются неудачными;
− производится сбрызгивание картофеля питательным раствором с заранее заданным интервалом в зависимости от фазы роста с одновременным контролем уровня влажности;
− производится увеличение значения pH с одновременным контролем значения параметра рН;
− все действия производятся при необходимой температуре и уровне аэрации;
− эксперимент заканчивается при увядании куста картофеля;
− оценивается общая масса с куста картофеля, средняя масса одной картофелины и их количество.
Результаты исследования и их обсуждение
В результате проведения эксперимента были получены оптимальные значения технологических параметров для каждой из фаз.
Для первой фазы было выяснено, что наибольшее число здоровых ростков картофеля было получено при значениях:
pH = 6,5;
H = 52 %;
T = 23ºC.
При отклонении от этих значений наблюдались гнилостные новообразования и/или увядание растений.
В нормальных условиях картофель сорта «Розара» образует 15–18 клубней. Для второй фазы наибольшее количество клубней получено при значениях:
pH = 6,5;
H = 54 %;
T = 21ºC.
Для третьей фазы наибольший вес был достигнут при значениях:
pH = 6,5;
H = 51 %;
T = 19ºC.
В результате трехпараметрической аппроксимации было выяснено, что наибольшую точность для первой фазы эксперимента обеспечивает полином следующего вида:
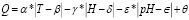,(3)
где Q – искомый результат;
T – температура;
H – влажность;
pH – параметр среды pH;
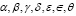– свободные коэффициенты.
Наибольшую точность для второй фазы эксперимента обеспечивает полином следующего вида:
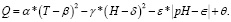(4)
Наибольшую точность для третьей фазы эксперимента обеспечивает полином следующего вида:
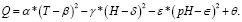(5)
При помощи программы, написанной на языке Python, были подобраны коэффициенты для каждой из фаз эксперимента.
В результате уравнение (3) для первой фазы эксперимента приняло следующий вид:
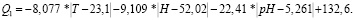(6)
График, описывающий уравнение (6), представлен на рис. 1.
Для второй фазы уравнение (4) имеет следующие коэффициенты
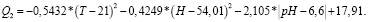(7)
График, описывающий уравнение (7), представлен на рис. 2.
На третьей фазе уравнение (5) имеет следующие коэффициенты
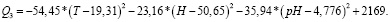(8)
График, описывающий уравнение (8), представлен на рис. 3.
Математическое описание процесса аэроаквапоники
|
Полином |
Максимальная приведенная ошибка |
|
|
1 фаза |
|
4,4 % |
|
2 фаза |
|
3,4 % |
|
3 фаза |
|
4,2 % |
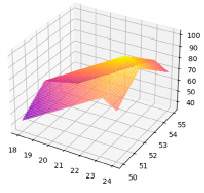
Рис. 1. График на основе уравнения (6)
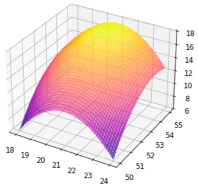
Рис. 2. График на основе уравнения (7)
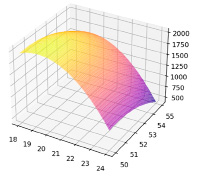
Рис. 3. График на основе уравнения (8)
Для определения адекватности полученного математического описания были рассчитаны приведенные погрешности для каждого из полученных полиномов.
Результаты расчетов в таблице.
В результате поиска теоретического экстремума были получены максимальные значений производительности для каждой фазы.
Для первой: pH = 6,5, H = 52 %, T = 23ºC, экстремальное значение полинома Q = 100, из чего следует, что при данных параметрах 100 % картофелин прорастут.
Для второй фазы: pH = 6,6, H = 54 %, T = 21ºC, экстремальное значение полинома Q = 18, из чего следует, что на каждом из проросших кустов завяжется по 18 клубней картофеля.
Для третьей фазы: pH = 6,5, H = 51 %, T = 19ºC, экстремальное значение полинома Q = 2062 г урожая с каждого куста картофеля.
Выводы
1. В результате использования экспериментального метода определения характеристических зависимостей количества производимого картофеля от параметров, влияющих на качество процесса выращивания, определено, что характер зависимости объема производимой продукции от температуры, влажности и параметра pH имеет экстремальную зависимость.
2. Определены полиномиальные зависимости, описывающие влияние температуры, влажности и параметра pH на развитие картофеля для каждого из этапов эксперимента, и определена максимальная ошибка, не превышающая погрешности измерения технологических параметров в 5 %, что свидетельствует об адекватности математического описания.