При движении летательного аппарата, в частности при его замедлении, тормозные элементы подвергаются высокому температурному воздействию, в связи с этим для получения высокого качества торможения дисковых механизмов необходимо выявить температурные значения элементов, участвующих в этом процессе. Такие результаты исследований используются для выбора материала и конструктивного исполнения при проектировании элементов трения, для последующего знания о количестве необходимых замедляющих движение устройств, которые впоследствии будут установлены в опоры летательных аппаратов. Получаемые результаты также способствуют получению взаимосвязи между параметрами, характеризующими энергетические данные тормозного узла, и температурными характеристиками трущихся элементов.
Для исследования возможности повышения физико-механических свойств материалов, используемых в изготовлении тормозных элементов, за счет технологических мероприятий будем считать, что торможение прекращается, как правило, при постоянной прижимающей силе, однако коэффициент трения фрикционных материалов, используемых в современных тормозах, изменяется в зависимости от скорости. Из-за этого тепловой расчет очень сложен. Торможение прекращается, как правило, постоянной силой давления, однако коэффициент трения фрикционных материалов, используемых в современных тормозах, изменяется нелинейно в зависимости от скорости.
Математически процесс торможения записывается в виде уравнения Фурье [1-3]:
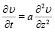, (1)
где a – коэффициент теплопроводности материала, который определяется как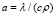 
; λ – коэффициент теплопроводности; с, ρ – удельная теплоемкость и соответственно плотность материала для изготовления тормозных элементов; z – глубина в элементе перпендикулярно поверхности контакта трущихся тел.
Уравнение (1) показывает связь между изменением температуры со временем с ее распределением в пространстве, перпендикулярном поверхности контакта трущихся деталей.
Материал и методы исследования
Далее необходимо рассмотреть процесс торможения, взяв за пример нагрев фрикционных элементов и их полупространства тепловым потоком q, при этом сам тепловой поток математически выражается через выражение (1), имеющую граничные условия второго рода [4-6]:
; 
,
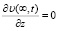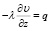а также при начальном условии, что:
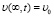. (2)
В случае неограниченной пластины. При одномерном нагреве постоянным тепловым потоком (q = const) тепловой режим описывается краевой задачей (1).
В теоретическом случае безразмерного элемента торможения и при равномерном прогреве, а также при постоянном тепловом потоке, т.е. q = const, тепловой режим будет описан уравнением (1) с граничными условиями:
; 
,
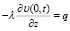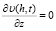и начальным условием:
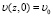. (3)
Рассмотрим решение данной задачи (1) с граничными условиями первого рода на диске: при z = 0; υx = υ0, где υ0 – начальная температура – является известной.
Тогда для граничных условий при необходимой толщине материала возьмем:
z = h; υx = 0.
А в качестве начального условия:
t = 0; υx = 0, (0 < z < h),
где υ0 – начальная температура (известная).
Дифференциальное уравнение с начальными и граничными условиями представляет собой параболическое уравнение.
Таким образом, уравнение (1) с граничными и начальными условиями представляет собой математическую модель рассматриваемого нестационарного процесса. Для этого заменим функцию:
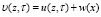, (4)
где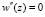 
и w(z) которые должны удовлетворять граничным условиям
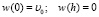, (5)
при этом функция u(x, τ) должна удовлетворять условию:
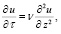(6)
которая имеет однородные граничные условия:
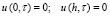, (7)
а также начальные условия, которое находятся из
,
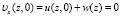откуда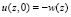 
. (8)
Рассмотрим уравнение Лапласа в дифференциальном виде:
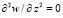, (9)
которое также соответствует граничным условиям (5).
При этом результат решения уравнения (3) запишем в виде w = Az + B; с учетом граничных условий вычислим значения А и В.
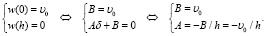
Получим, что:
.
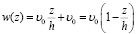Найдем решение уравнения (6), которое имеет однородные граничные условия (7), а также начальные условия (8):
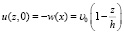(10)
Для решения уравнения (6) необходимо получить произведения пары функций, причем одна является функцией зависимости от τ, другая от x.
Такое решение называется методом разделения переменных:
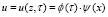(11)
После подстановки уравнения (11) в дифференциальное уравнение получим:
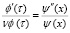(12)
Такое может быть, если оба отношения равны постоянному числу λ:
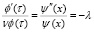(13)
В результате решения уравнений получим:
.
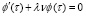
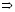
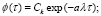
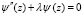
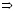
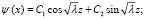
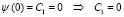
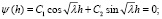
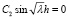
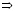
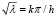
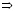
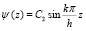Тогда:
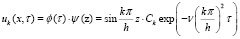(14)
Сумму решений можно представить в виде ряда:
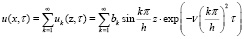(15)
Уравнение (15) по условию должно удовлетворять начальному (3):
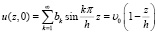(16)
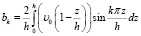(17)
Для нахождения коэффициентов bk, интегрируя по частям, находим:
; 
;
;
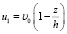
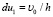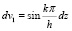
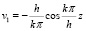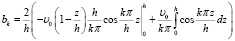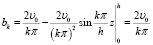. (18)
Подставляя значение bk в (14), получим:
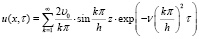(19)
Окончательно решение уравнения (1) будет иметь вид:
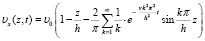(20)
Ограничимся двумя членами этого ряда, тогда получим:
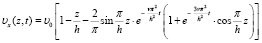(21)
Для анализа полученных зависимостей найдем отношение температур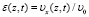 
по толщине диска в различные моменты времени:
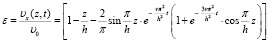(22)
Результаты исследования и их обсуждение
Из формулы (22) и рисунка 1 видно, что при значениях времени t в до 10 секунд режим изменения температуры является установившимся, а изменение температуры по оси z примет вид:
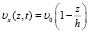(23)
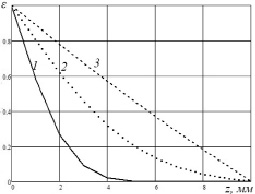
Рисунок 1 – Зависимость относительной температуры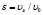 
от координаты z по температурному нагреву слоя диска в различные моменты времени: 1 – t = 1 c; 2 – t = 3 c; 3 – t = 10 c.
Результаты исследований теоретического расчета изменения температуры на поверхности трения тормозного диска
Для описания процесса торможения на примере фрикционного элемента рассмотрим нагревание постоянным тепловым потоком q, который описывается краевой задачей (1) с граничными условиями второго рода [7, 8]:
; 
,
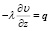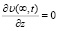и начальным условием: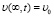 
.
Решение данной задачи описывается следующими зависимостями:
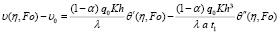, (24)
где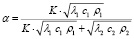 
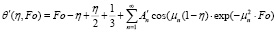(25)
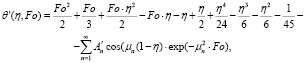(26)
где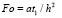 
, 
, 
, 
, 
, 
.
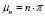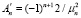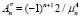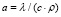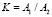Также на основе поставленной задачи был проведен тепловой расчет тормозного диска на примере пары трения «тормозной диск и тормозная колодка».
Расчеты проводились для диска, так как его материал имеет гораздо большую теплопроводность, чем материал колодок, и, соответственно, подвергается большим термическим нагрузкам. Тормозной диск изготовлен из стали. Толщина диска 40 мм. Внешний диаметр диска составляет 640 мм.
Тормозная колодка изготавливается из металлокерамического материала. Площадь ее 364 см2. Толщина материала составляет 22 мм, при этом минимальная толщина материала для эксплуатации составляет 5 мм. Коэффициент трения этой пары трения равен 0,3.
Во время экстренного торможения сила нажатия колодки на диск остается постоянной. Примем, что скорость трения V(t) и интенсивность тепловыделения при трении q(t) изменяются линейно в зависимости от времени торможения t [9, 10]:
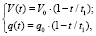(27)
где V0 – скорость трения в начале торможения; t1 – время торможения.
На поверхности трения η = 0 среднее приращение температур диска определяется как [11, 12]:
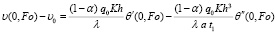; (28)
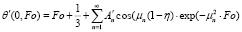; (29)
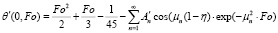, (30)
где α = 0,092 – коэффициент распределения теплового потока на колодку из тормозного механизма; 1 – α = 0,908 – коэффициент распределения теплового потока в тормозной диск; q(t) = 11565 (кВт/м2) – интенсивность тепловыделения на пятой секунде торможения; h2 = 0,02 м – толщина тормозного диска; К = 0,0364 / 0,1685 = 0,216 – коэффициент взаимного перекрытия колодки и диска; λ2 = 43 Вт/(м∙град) – теплопроводность диска.
Исследования теоретического расчета температур на поверхности трения диска при экстренном торможении приведены на рисунках 2 и 3.
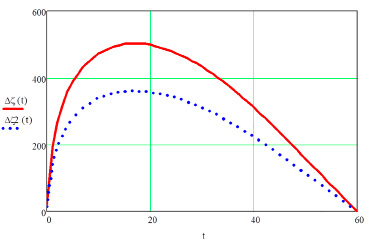
Рис. 2. Изменение приращений температур тормозного диска в зависимости от времени и коэффициента теплопроводности при переменном тепловом потоке: λ2 = 43 Вт/(м∙град) – сплошная линия; λ2 = 60 Вт/(м∙град) – пунктирная линия
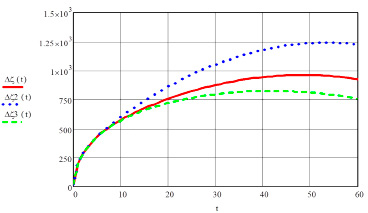
Рис. 3. Изменение приращений температур тормозного диска в зависимости от времени и толщины диска при постоянном тепловом потоке: h2 = 20 мм – сплошная линия; h2 = 25 мм – пунктирная линия; h2 = 15 мм – штрих-пунктирная линия
Заключение
Из графиков на рисунках 2 и 3 видно, что при увеличении толщины диска и коэффициента теплопроводности материала тепловая нагрузка на тормозную систему уменьшается.
Полученные результаты позволяют констатировать, что максимальная температура тормозного диска при h2 = 20 мм достигает 961°С за 50 с при экстренном торможении, а к концу торможения снижается до 927°С за 60 с. При этом в начальный момент торможения, на 5-й секунде температура вырастает до 388ºС.