Регрессионный анализ в настоящее время успешно применяется для решения широкого круга различных прикладных задач (см., например, [1-3]). А запас методов регрессионного анализа постоянно расширяется – появляются новые спецификации регрессионных моделей, методы их оценивания и критерии адекватности. Так, в работе [4] впервые была введена неэлементарная линейная регрессия (НЛР), регрессорами в которой выступают как объясняющие переменные, так и все возможные комбинации их пар, преобразованные с помощью бинарных операций min и max. В той же работе предложен алгоритм их приближенного оценивания с помощью метода наименьших квадратов (МНК). В [5] рассмотрены некоторые стратегии построения НЛР, основанные на переборных процедурах. А в [6] задача выбора оптимальной структуры НЛР сведена к задаче частично-булевого линейного программирования. До сегодняшнего дня рассматривались лишь НЛР, содержащие в каждом аргументе бинарной операции только одну объясняющую переменную.
Цель исследования состоит в формализации новой спецификации НЛР, разработке алгоритма её МНК-оценивания и решении задачи моделирования сельскохозяйственной продукции в Республике Бурятия.
Материал и методы исследования
НЛР с бинарными операциями min и max, впервые введенная в [6], имеет следующий вид:
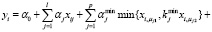
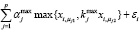
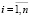, (1)
где n – объем выборки; l – число входных переменных; yi – i-е значение выходной переменной; xij – i-е значение j-й входной переменной; min (max) – бинарные операции, возвращающие минимум (максимум) двух чисел; 
– число всех возможных комбинаций пар входных переменных; μj1, μj2,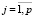 
– элементы первого и второго столбца матрицы M размера p×2, содержащей по строкам в лексикографическом порядке индексы всех возможных комбинаций пар входных переменных; αj , 
, 
, 
, 
, 
, 
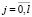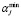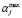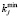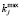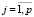– неизвестные параметры; εi – i-я ошибка аппроксимации.
Для обобщения модели (1) рассмотрим часто применяемую в экономике производственную функцию Леонтьева [7]:
, 
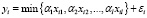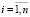. (2)
Модель (2) можно обобщить, используя в аргументах операции min линейные комбинации объясняющих переменных:
, 
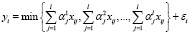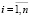. (3)
Аргументы в модели (3) естественным образом должны быть различны, т.е. в них не должно быть одинаковых линейных комбинаций объясняющих переменных. Также в регрессии (3) каждый аргумент должен срабатывать хотя бы 1 раз.
Пусть операция min в (3) является бинарной, т.е. содержит 2 аргумента. Тогда модель (3) примет вид:
, 
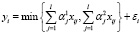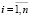. (4)
Для (4) будем считать, что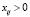 
, 
, 
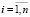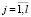, а все объясняющие переменные коррелируют с y с одинаковым знаком, т.е. оценки параметров 
, 
, 
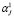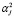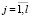либо только положительны, либо только отрицательны. Тогда за знак операции min в (4) можно вынести общий множитель:
, 
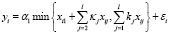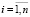, (5)
где κ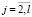j, 
, kj,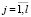 
– неизвестные положительные параметры.
Добавим в модель (5) свободный член α0:
, 
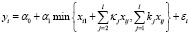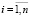. (6)
Приближенно найти МНК-оценки модели (6) можно по следующему алгоритму.
Найти область D возможных значений параметров κ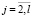j, 
, kj,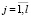 
.
Разбивая область D точками, определить для каждой из них МНК-оценки параметров α0 и α1 модели (6).
Выбрать оценки, для которых сумма квадратов остатков минимальна.
Область D идентифицируется по следующему алгоритму.
Находится область D1 значений параметров κ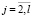j, 
, kj,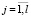 
, в которой срабатывает только первый аргумент бинарной операции в (6). Для этого необходимо решить систему линейных неравенств:
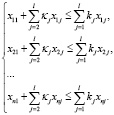
Находится область D2 значений параметров κ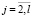j, 
, kj,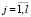 
, в которой срабатывает только второй аргумент бинарной операции в (6). Для этого решается система линейных неравенств:
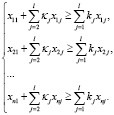
В условиях неотрицательности параметров κ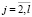j, 
, kj,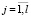 
, находится открытая область D как инверсия объединения областей D1 и D2.
Пусть в модель (6) каждая объясняющая переменная входит ровно 1 раз. Тогда сколько комбинаций различных регрессий можно из неё составить? Число переменных l можно разбить на 2 аргумента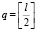 
способами, где [z] – целая часть числа z. Пусть все эти разбиения содержатся в матрице V = {vij} размера q×2. Тогда по этой матрице можно вычислить общее количество регрессий по формуле 
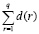, где
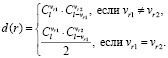
Просуммируем все эти уравнения, получив следующую модель:
, 
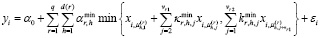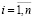, (7)
где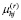 
– элементы матрицы M(r) размера d(r)×l, содержащей все возможные комбинации переменных для их r-го разбиения.
Например, если l = 4, то спецификация (7) принимает вид:
, 
.
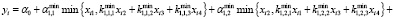
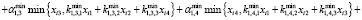
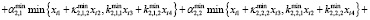
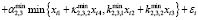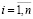В модели (7) в каждую бинарную операцию min входит ровно l объясняющих переменных. Расширим эту регрессию регрессорами с бинарными операциями min, содержащими 2, 3, ..., l–1 переменных:
, 
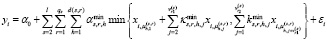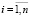, (8)
где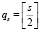 
, 
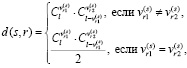
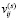– элементы матрицы V(s) размера qs×2, содержащей все разбиения числа s по 2, 
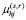– элементы матрицы M(s,r) размера d(s,r)×l, содержащей все возможные комбинации s переменных для их r-го разбиения.
Тогда с использованием спецификации (8) введем НЛР с линейными комбинациями переменных в аргументах бинарных операций:
, 
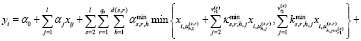
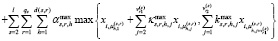. (9)
Очевидно, что если в (9) взять s = 2, то эта модель вырождается в НЛР (1).
Приближенные МНК-оценки регрессии (9) можно найти с использованием описанного выше алгоритма.
Результаты исследования и их обсуждение
Сформулированные в этой работе НЛР (9) были использованы для моделирования продукции сельского хозяйства в Республике Бурятия. Стоит заметить, что моделирование и прогнозирование сельскохозяйственной продукции является актуальной научной задачей. Решению этой проблемы посвящено множество научных работ. Так, например, в [8] построена модель регрессии зависимости стоимости произведенной продукции от объема затрат на неё в Саратовской области, в [9] – модель сельскохозяйственной продукции в Оренбургской области, в [10] – модели производства основных видов продукции сельского хозяйства в Республике Дагестан, в [11] – модель производства молочной продукции в Республике Крым.
Для построения НЛР были использованы ежегодные статистические данные (https://rosstat.gov.ru/) за период с 2000 по 2021 г. по следующим переменным:
y – продукция сельского хозяйства в Республике Бурятия (млн руб.);
x1 – урожайность овощей (центнеров с одного га убранной площади);
x2 – производство скота и птицы на убой (в убойном весе, тыс. тонн);
x3 – надой молока на одну корову в сельскохозяйственных организациях (кг).
Все объясняющие переменные тесно коррелируют с y со знаком «+».
Сначала с помощью МНК было получено уравнение линейной регрессии:
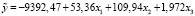. (10)
Коэффициент детерминации R2 модели (10) составил 0,942, что позволяет судить о её весьма высоком качестве.
Затем с помощью МНК оценивались следующие спецификации НЛР:
, 
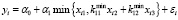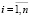, (11)
, 
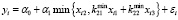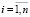, (12)
, 
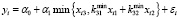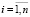. (13)
Оценивание моделей (11) – (13) проводилось с использованием специально разработанного скрипта для эконометрического пакета Gretl.
Для каждой из моделей (11) – (13) предварительно была найдена область возможных значений параметров, входящих в бинарные операции. Для параметров k11 и k12 модели (11) эта область представлена на рис. а, для k21 и k22 модели (12) – на рис. б, для k31 и k32 модели (13) – на рис. в.
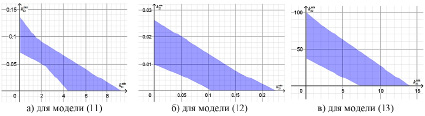
Области возможных значений параметров
Затем для каждой области (рисунок) были выбраны прямоугольники, у которых координаты левого нижнего угла (0,0), а координаты правого верхнего угла (9.343044,0.136461), (0.225949,0.026446) и (14.0987,100.2632) соответственно, т.е. эти прямоугольники целиком «покрывают» найденные области. После чего прямоугольники равномерно разбивались на 10 000 точек. Каждая точка проверялась на предмет попадания в соответствующую область, и, в случае попадания, находились МНК-оценки параметров α0 и α1 регрессий (11) – (13). Далее из каждой области выбиралась точка, обеспечивающая минимум суммы квадратов остатков НЛР. В итоге были получены следующие оцененные модели (11) – (13):
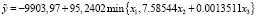, (14)
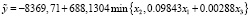, (15)
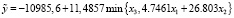. (16)
Для НЛР (14) R2 = 0,9388, для (15) R2 = 0,9608, для (16) R2 = 0,9755. Таким образом, модель (16) оказалась самой лучшей из регрессий (14) – (16) по величине коэффициента детерминации. Она также лучше линейной регрессии (10). Заметим, что дополнительно проводилось оценивание моделей (11) – (13) с бинарной операцией max. Однако по величине R2 все они оказались хуже зависимости (16).
Как видно, в уравнении (16) знаки всех коэффициентов удовлетворяют смыслу решаемой задачи, поэтому полученную модель можно интерпретировать. Для этого представим её в кусочно-заданной форме:
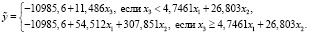
Тогда справедлива следующая интерпретация. Если линейная комбинация урожайности овощей x1 и производства скота и птицы x2 (4,7461x1 + 26,803x2) превосходит надои молока на одну корову x3, то на продукцию сельского хозяйства в Республике Бурятия y влияет только x3. Так происходило в 2000–2003 гг. и в 2014 году. При этом с увеличением x3 на 1 кг y увеличивается примерно на 11,486 млн руб. Если линейная комбинация 4,7461x1 + 26,803x2 не превосходит x3, то на y влияют и x1, и x2. Так происходило в 2004–2013 гг. и в 2015–2021 гг. При этом с увеличением x1 на 1 центнер y увеличивается примерно на 54,512 млн руб., а с увеличением x2 на 1 тыс. тонн увеличивается примерно на 307,851 млн руб.
Заключение
В результате проведенных исследований были предложены неэлементарные линейные регрессии с линейными комбинациями переменных в аргументах бинарных операций. Предложенные модели содержат большое число неизвестных параметров, что делает их довольно гибким инструментом регрессионного моделирования. Разработан алгоритм их численного МНК-оценивания. С помощью предложенных моделей успешно решена задача моделирования сельскохозяйственной продукции в Республике Бурятия. Дальнейшие работы автора будут связаны с разработкой универсального программного обеспечения для оценивания предложенных регрессий.