Шероховатость поверхности является нормированным показателем и наиболее часто применяемой характеристикой качества поверхности. В большинстве случаев по шероховатости поверхности в конструкторских и технологических документах проставляется требование только к высотным параметрам шероховатости: либо среднеарифметическое отклонение профиля (Ra, мкм), либо шероховатость по 10 точкам (Rz, мкм). Однако данные величины далеко не полностью характеризуют профиль поверхности. В целом следует сказать, что проблема описания шероховатости поверхности на сегодняшний день полностью не решена. Принципиально для решения этой задачи используются два подхода. Первый подход можно назвать параметрическим [1]. Он предполагает, что описание шероховатости поверхности реализуется за счет использования некоторой системы числовых параметров. Второй подход [2] для того, чтобы характеризовать профиль шероховатости поверхности по таким категориям, как распределение тангенсов углов наклона боковых сторон профиля, функция распределения высот профиля, функция, которая описывает опорную кривую, и т.д.
Наиболее широко в отечественной практике применяется оценка шероховатости поверхности с использованием параметров, которые регламентированы ГОСТ 2789. Данный нормативный документ предполагает использование как высотных параметров (Ra, Rz, Rmax), так и шаговых (S, Sm) и опорных (tp). Кроме того, в стандарте предусмотрена возможность указания особенностей геометрии профиля (например, направление неровностей). Однако возможна только качественная оценка данных аспектов профиля.
ИСО 4281/1-1984 – Международный стандарт, который расширяет набор параметров для оценки шероховатости поверхности, прописывая не только масштабные факторы, но и количественные параметры формы и расположения неровностей. Для этих целей используются величины среднеарифметического наклона неровностей Δа и среднеквадратического наклона неровностей Δq. Данные параметры определяются по следующим расчетным зависимостям:
,
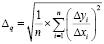
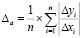где x, y – соответственно абсцисса и ордината точек на кривой профилограммы поверхности.
В целом можно сказать, что на сегодняшний день используется более 50 параметров для характеристики шероховатости поверхности. Общим недостатком параметрического подхода к описанию шероховатости поверхности является то, что ни одна система параметров не дает исчерпывающего описания профиля и, кроме того, параметрический подход неприменим при решении ряда задач по конструированию (например, исследования герметичности, контактного взаимодействия и т.д.).
Исследования в части описания шероховатости поверхности посредством непараметрического подхода были выполнены в работах В.Э. Завистовского и С.Э. Завистовского [3]. При этом делалось допущение, что высотные значения микропрофиля имеют подчинение нормальному закону распределения. Дальнейшее развитие данный подход получил в работах научной школы под руководством Ю.Р. Виттенберга [4], где для характеристики шероховатости поверхности были использованы корреляционные функции. При этом параметры шероховатости можно получить из соотношений вида:
,
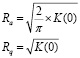где К(0) – значение автокорреляционной функции профиля в нулевой точке.
Моделям, которые приведены выше, присущи те же недостатки, что и параметрическому подходу. В работах научной школы И.В. Крагельского, Н.Б. Демкина и др. [5] шероховатость поверхности рассматривается как совокупность геометрических примитивов. Такой подход позволил решать задачи оценки исследования эксплуатационных свойств поверхностей. Однако недостатком подхода является то, что кривая профиля является детерминированной, и не учитываются структурные свойства профиля.
В последнее время все большее распространение при моделировании геометрических объектов получает фрактальная геометрия. Применению теории фракталов при моделировании профилей и поверхностей деталей посвящены исследования [6; 7]. Весьма неплохие результаты при моделировании шероховатости поверхности дает метод случайных сложений [7]. Однако в работе [7] показано, что использование нормального распределения в чистом виде не позволяет обеспечить требуемую точность. Поэтому в работе [7] была произведена корректировка алгоритма, которая фактически заключалась в подгонке закона под реальные профили поверхностей. Недостатком такого решения является то, что оно не универсально и требует индивидуального подхода применительно к каждому конкретному случаю. Например, результаты, полученные в работе [7], справедливы только для поверхностей, обработанных чистовым точением. Поэтому необходимо провести исследования и подобрать закон распределения, которому подчиняются высоты шероховатости поверхностей с регулярным профилем, которые обработаны разными методами (точением и выглаживанием).
Цель исследования: повышение точности моделирования шероховатости поверхностей с регулярным профилем за счет модернизации алгоритма построения фрактальной кривой.
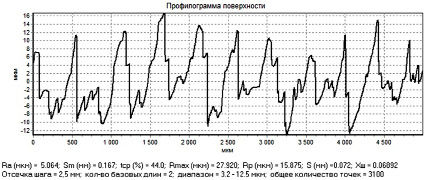
Рис. 1. Профилограмма поверхности
Материал и методы исследования
В качестве исходных данных были использованы значения высот профилей шероховатости поверхностей, обработанных на токарном станке чистовым точением и алмазным выглаживанием. Измерение шероховатости поверхностей осуществлялось при помощи профилометра-профилографа марки «Абрис ПМ-7». Пример профилограммы обработанной поверхности приведен на рисунке 1.
Полученные значения координат профиля были использованы в качестве исходных данных для проверки гипотезы о соответствии закону распределения. Проверялись следующие законы.
1. Нормальный закон распределения, параметры которого определяются по известным зависимостям [8]:
,
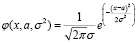где a, σ – параметры закона распределения.
2. Закон распределения Вейбула [8]:
,
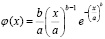где a, b – параметры закона распределения.
3. Закон распределения Рэлея [8]:
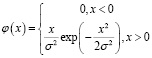
4. Закон распределения Накагами [8]:
,
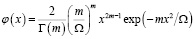где Г(m) – гамма-функция; m, Ω – параметры закона распределения.
При этом параметр m можно получить из следующего выражения:
,
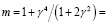
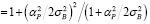где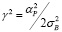 
– параметр, который отражает соотношение детерминированной (σр) и стохастической (σв) составляющих.
При этом значения σВ и σР можно получить на основе корреляционного анализа профилограмм поверхностей и определения реализации автокорреляционной функции KXX(t). Выражения для вычисления составляющих корреляционной функции имеют вид [7]:
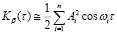
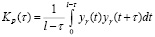
Параметры σВ и σР соответствуют значениям Kβ(0) и Kр(0).
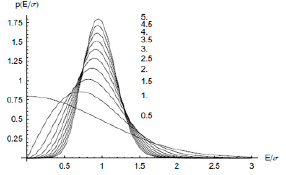
Рис. 2. Зависимость формы кривой закона распределения Накагами от параметра m
При этом можно отметить, что закон распределения Накагами обладает важным свойством: при изменении параметра m он переходит в нормальный (рис. 2).
Проверка соответствия закона распределения осуществлялась по критерию Колмогорова – Смирнова [8].
Построение фрактальной модели шероховатости поверхности осуществлялось на основе использования метода случайных сложений [7]. При этом укрупненно последовательность вычислений выглядит следующим образом.
1. В качестве начальных значений абсцисс профиля принимаются величины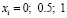 
.
2. Начальные значения ординат в данных точках принимаются нулевыми.
3. Генерируются значения ординат и прибавляются к исходным. При этом по умолчанию используется генератор с распределением Гаусса.
4. Полученные значения ординат усредняются согласно зависимости вида:
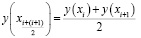
5. Осуществляется корректировка параметров рассеяния:
,
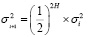где Н – эмпирический показатель Херста. В данном случае показатель Херста является оценкой величины фрактальной размерности D, т.к. данные величины между собой связаны выражениями вида:
– для плоских объектов: D = 2 – H;
– для объемных объектов: D = 2 – H.
6. Определяются новые значения абсцисс посредством усреднения предыдущих значений.
Результаты исследования и их обсуждение
На рисунке 3 приведены примеры расчетов параметров законов распределения.
Аналогичным образом строились кривые распределения и для других рассматриваемых законов. Ввиду отсутствия закона распределения Накагами в стандартных пакетах статистического анализа, расчеты проводились в авторской компьютерной программе. В результате статистической обработки более 150 профилограмм поверхностей было установлено, что, по критерию согласия Колмогорова – Смирнова, шероховатость поверхности соответствует закону распределения Накагами и не соответствует трем другим рассматриваемым. Был реализован генератор ординат фрактальной модели профиля на основе закона распределения Накагами. На рисунке 4 приведены примеры смоделированных двухмерного профиля и трехмерной шероховатой поверхности.
Для оценки точности получаемых результатов производилось моделирование профилей с исходными параметрами, которые были определены по реальным объектам (взяты с реальных профилограмм). Затем по полученным фрактальным кривым определялись параметры шероховатости поверхности в соответствии с ГОСТ 2789.
На рисунке 5 приведен пример результатов определения параметров по ГОСТ 2789 для реальных профилей, моделей, построенных с использованием генератора ординат профиля на основе закона распределения Гаусса (нормального) и закона распределения Накагами.
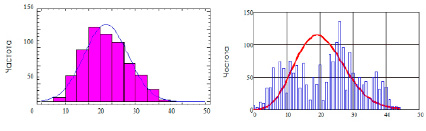
а б
Рис. 3. Результаты расчетов: а – нормальное распределение; б – распределение Накагами
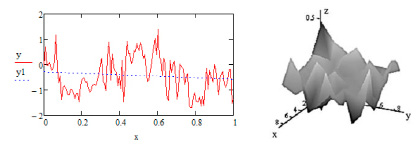
а б
Рис. 4. Пример результатов моделирования: а – фрактальная кривая профиля шероховатости; б – поверхность
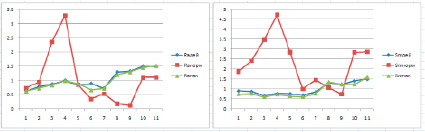
а б
Рис. 5. Пример точности моделей: а – значения Ra для реальных профилей и модели; б – то же для Sm
Как можно видеть из рисунка 5, использование генератора ординат профиля на основе закона распределения Гаусса дает значительную погрешность (более 25%). Генератор ординат на основе закона распределения Накагами позволяет получать погрешность, не превышающую 10%, что вполне достаточно для решения как задач описания шероховатости поверхности, так и при решении прикладных задач, связанных с исследованием эксплуатационных свойств.
Заключение
В результате статистического анализа профилограмм поверхностей, имеющих регулярный микропрофиль, доказано, что их ординаты подчиняются закону распределения Накагами. Реализация генератора ординат профиля на основе использования закона распределения Накагами позволяет получать фрактальные модели шероховатости поверхностей с погрешностью, которая не превышает 10%. Важным преимуществом является универсальность генератора в части моделирования профилей и трехмерных поверхностей деталей, которые обработаны чистовым точением и алмазным выглаживанием с жестким закреплением индентора без применения окон сглаживания [7]. Совместное использование фрактальной геометрии и закона распределения Накагами позволяет учесть как структурные особенности текстуры профиля (через значения фрактальной размерности), так и технологические аспекты ее формирования (через соотношение детерминированной и случайной составляющей).
Применение разработанной модели принципиально возможно при решении задач, не связанных с теми, которые рассматривались в данной статье. В частности, при помощи разработанного инструментария можно моделировать микропрофили дорог [9; 10] и других шероховатых объектов в разных областях практики моделирования.