Проблематика развития вероятностного подхода к математическому моделированию в области научных исследований и технических разработок является весьма актуальной. Можно указать для примера только самые востребованные в аспекте разработки вероятностных и статистических моделей направления: медицина [1], энергетика [2], химические технологии, в первую очередь связанные с нефтегазовым комплексом [3], информационные технологии [4], анализ бизнес-процессов [5] и т.д. В то же время, с точки зрения работодателей, именно построение математических моделей является слабым местом подготовки инженеров и экономистов в современных условиях. Это не вызывает удивления по двум основным причинам. Во-первых, на освоение курса теории вероятности, а иногда и математической статистики, в типовых учебных планах большинства инженерных направлений подготовки отводится один семестр, что не дает преподавателям возможности охватить весь материал, научить решать задачи по теории вероятностей и одновременно углубиться в вопросы построения вероятностных моделей явлений окружающего мира с анализом их точности и границ применимости. Во-вторых, освоение вероятностных университетских дисциплин преимущественно на 1–2 курсах осложняет ориентацию задач на будущую профессиональную деятельность инженеров и экономистов [6]. Авторы встречались с различными подходами к формированию смыслового и содержательного компонентов заданий по теории вероятностей: от строго классического, лишенного какого-то ни было эмоционального окраса, до ёрнического, в духе «Вредных советов» Григория Остера. Авторские попытки увязать содержание задач с инженерной и экономической проблематикой привели к продуцированию громоздких и скучных для студентов заданий. Можно рекомендовать остановиться на «умеренных» текстах житейской и студенческой тематики либо опираться на общекультурные ориентиры [7]. Вопросы выбора содержания текста задач важны, поскольку связаны с поддержкой мотивации к изучению вероятностных дисциплин, однако они не могут решить проблем формирования компетенций студентов в области построения и анализа математических моделей, которым и посвящено настоящее исследование.
Материалы и методы исследования
Настоящая работа продолжает исследования авторов, направленных на поиск механизмов формирования системного, в частности вероятностного, подхода студентов к научному познанию [8, 9]. В качестве соавторов работ были приглашены иностранные обучающиеся программ предмагистерской подготовки Санкт-Петербургского политехнического университета Петра Великого (СПбПУ). Подготовку иностранных граждан к освоению основных образовательных программ на русском языке осуществляют несколько сотен российских вузов, но менее двух десятков из них реализуют специализированные образовательные программы подготовки в магистратуру и аспирантуру. Дело в том, что для запуска и функционирования таких программ необходима численность контингента иностранных подготовительных отделений в несколько сотен обучающихся. Кроме того, такая подготовка имеет смысл только при условии формирования проектных исследовательских компетенций [10] будущих магистрантов, что требует наличия специально подготовленных научно-педагогических кадров. Именно в предмагистратуре преподаватели могут сосредоточиться на анализе вероятностных моделей, опираясь на сформированные в зарубежных вузах компетенции обучающихся в области теории вероятностей и математической статистики.
С помощью предмагистрантов авторы выполнили в предшествующие годы два исследования в области точности вероятностных моделей. Тематика формирования компетенций студентов в этой области представляется актуальной, что подтверждается, в частности, работами других авторов [11, с. 109–116].
В работе [12], выполненной в 2020 г. с помощью предмагистранта из Сирии, авторы, прежде всего, получили графическое подтверждение приближения формы полигона биномиального распределения в существенно несимметричном случае к форме кривой Гаусса. Эти графики были включены авторами в тексты лекций по теории вероятностей для российских и иностранных студентов 2-го курса, что позволило подойти в этих лекциях к проблеме оценки точности приближенных вычислений в теории вероятностей. Далее в этой же работе авторы провели сравнение значений вероятностей, вычисленных на интервалах, по точным формулам Бернулли и приближенным формулам, следующим из интегральной теоремы Лапласа. Такие же вычисления были проделаны для случая редких событий на основе сравнения результатов, полученных по точной формуле Бернулли и приближённым формулам Пуассона и Лапласа. Выбор распределений Бернулли и Пуассона объясняется тем, что, по мнению исследователей, именно эти распределения являются наиболее важными во множестве случаев практических приложений [13]. Несмотря на результаты, подтверждающие возможность замены расчётов по формуле Бернулли расчётами по формуле Пуассона уже при 20 измерениях, сами величины относительной ошибки нельзя было признать удовлетворительными. Это, во-первых, позволило использовать полученные результаты только как качественные, тем более что было получено подтверждение положения общей теории ошибок С.Г. Михлина об обратно корневом убывании ошибки с ростом числа измерений. Во-вторых, это же обстоятельство породило необходимость дальнейшего исследования точности вероятностных моделей Пуассона, аппроксимирующих формулу Бернулли с детальным анализом поведения абсолютной и относительной ошибок вычислений. Такое исследование было проведено авторами в 2021 г. с помощью предмагистрантов из Сирии и из Греции [14].
В этой работе было показано, что при вероятности наступления редкого события р = 0,005 наихудшее значение абсолютной ошибки достигается для Р (Х = 1) и не превышает 0,12 %, в то время как при вероятности наступления редкого события р = 0,0002 наихудшее значение абсолютной ошибки также достигается для Р (Х = 1), но не превышает 0,005 %. Таким образом, студентам можно демонстрировать положение, что точность формулы Пуассона существенно повышается при уменьшении вероятности редкого события. Эти результаты можно было бы считать превосходными, если бы не характер поведения относительной ошибки, которая неуклонно возрастает. Это связано с накоплением ошибок округления при операциях с малыми величинами. Действительно, наихудшие значения относительной ошибки получаются при вычислении Р (Х = 4), для нахождения которой требуется произвести наибольшее число операций. Эти результаты также пригодны для использования в учебном процессе. Студентам можно продемонстрировать конкретные ограничения, связанные с приближенными вычислениями в теории вероятностей и математической статистике.
В настоящем исследовании авторы обратились к другой стороне оценки вероятностных моделей, связанной с проблемой ограниченности выбора. А именно, предмагистрантам было предложено сравнить результаты вычисления вероятности событий, связанных с выбором из бесконечного и конечного полей (банков). Бесконечный выбор определяется формулами Бернулли и/или теоремами о сложении и умножении вероятностей событий, конечный – формулами на основе классического определения вероятности. Эта проблематика связана с современными воззрениями на определения вероятности [15]. Точнее, сопоставляются классическое и статистическое определения вероятности. Эта проблема является многозначной, что находит отражение и в курсе теории вероятностей. Можно привести характерные примеры формулировок задач на сумму и произведение событий: «вероятность того, что цель будет засечена первым локатором, составляет 85 %», «вероятность выхода устройства из строя составляет 2 %», «вероятность аварии на атомной станции составляет 0,05 %» и т.д. Ясно, что эти примеры основаны на неких упрощенных статистических данных, однако студенты должны задуматься над тем, сколько опытов необходимо провести, чтобы быть уверенным в точности модели выбора из бесконечного банка. Например, какова была статистика аварий на атомных станциях, достаточна ли она для того, чтобы определение вероятности было статистическим, а не экспертным? С этой же проблематикой отчасти связана задача о минимальном объёме выборки в статистике. Таким образом вопросы, поднятые в настоящем исследовании, актуальны и представляют дидактический интерес в аспекте формирования вероятностного подхода в научном познании студентов.
Результаты исследования и их обсуждение
Исследование было проведено на базе следующей модельной задачи:
Летом 75 % дней солнечных. Построить ряд распределения числа солнечных дней из 3 выбранных (0, 1, 2 или 3).
Выбор тематики определяется нейтральным содержанием, что важно в интернациональных группах студентов. Кроме того, у обучающихся создаётся представление о реальной возможности накопления статистического материала за счет повторяющихся наблюдений. Очевидно, что для решения используется формула Бернулли
РВ(i) = 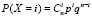
со значениями параметров
р = 0,75, q = 1 – p = 0,25, n = 3.
Это точное решение РВ(0), РВ(1), РВ(2), РВ(3).
Для исследования приближенных решений были использованы задачи с выбором на основе классического определения вероятности:
Из N = 12 дней m = 9 солнечных. Найти вероятности того, что среди этих 12 дней будет 0 солнечных, 1 солнечный, 2 солнечных, 3 солнечных.
Это будет приближенное решение РК(0), РК(1), РК(2), РК(3), которое находится по формуле
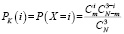
Для повышения точности приближённого решения находятся также значения обозначенных выше вероятностей для последовательности начальных условий: N = 16, m = 12; N = 20, m = 15; N = 40, m = 30; N = 60, m = 45; N = 80, m = 60; N = 100, m = 75. Для иллюстрации выбраны результаты крайних случаев грубого (N = 12, m = 9) и точного (N = 100, m = 75) приближённых решений по классической формуле. Соответствующие полигоны РК представлены на рис. 1 и 2 вместе с полигоном точного решения, полученного по формуле Бернулли РВ.
Очевидна сходимость приближённого решения к точному, причём ее характер можно наблюдать, рассмотрев последовательно все построенные полигоны. Наибольшее расхождение наблюдается для вероятности Р(2), но уже для N = 80, m = 60 оно не превышает 1 %.
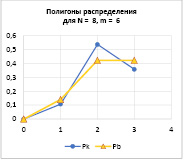
Рис. 1. Полигоны распределения по формуле Бернулли РВ и по классической формуле РК в грубом приближении
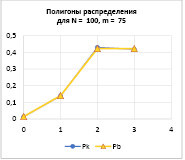
Рис. 2. Полигоны распределения по формуле Бернулли РВ и по классической формуле РК в точном приближении
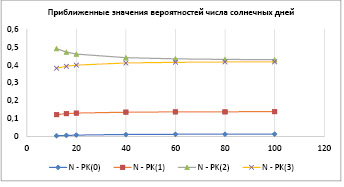
Рис. 3. Зависимость приближенных значений вероятностей РК(i) от объёма банка для выбора N
Таким образом, вероятно именно эти параметры можно считать приемлемыми для замены в условиях данной задачи выбора из бесконечного банка выбором из конечного банка. Разумеется, в случае расчётов параметра безопасной работы атомной станции необходима большая точность, а соответственно, и большие объёмы данных наблюдений.
Графики сходимости компонентов полигонов РК(i) представлены на рис. 3.
Видно, что все компоненты полигонов приближённых решений выходят на свои предельные (точные) значения снизу, и только наиболее грубые оценки Р(2) – сверху.
Для детального анализа сходимости приближенных значений вероятностей к точным были вычислены величины абсолютных ошибок Δ = PК – PВ (рис. 4) и относительных ошибок ε = Δ / PB (рис. 5) всех изученных случаев. Как и в предшествующих исследованиях авторов [12] и [14], величины абсолютных ошибок достигают долей процента с гарантией при N = 100, чего нельзя сказать о величинах относительных ошибок, остающихся в окрестности 10 %. Это объясняется, во-первых, выполнением деления малых величин, во-вторых, накоплением ошибок округления в связи с ростом числа операций. Ошибки округления становятся ведущим источником погрешности по сравнению с ошибками моделирования.
Были подобраны аппроксимации для графиков абсолютных и относительных ошибок. Оказалось, что
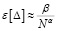 , = >
, = > 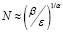 ,
,
где константа β варьируется от 1,2 до 8,1 для разных компонентов полигона РК(i) в случае относительной ошибки, или от 0,13 до 0,95 в случае абсолютной ошибки, а показатель α близок к 1, причём превышает 1 для трех компонентов из четырёх, что указывает на относительно быструю сходимость приближенного решения к точному.
Заключение
Проведенный анализ дает возможность сделать вывод о правомерности замены выбора из бесконечного банка вариантов выбором из конечного банка. Авторы провели анализ значений абсолютных и относительных ошибок приближенного вычисления вероятностей. Авторы показали, что уже при 100 вариантах выбора приближенные значения достаточно хорошо приближают точные. Это значит, что такое количество случаев оказывается достаточным для генерирования значений вероятности в соответствии со статистическим подходом к их определению. Эти данные могут быть использованы при прогнозировании бизнес-процессов и в теории надёжности при умеренных уровнях рисков.
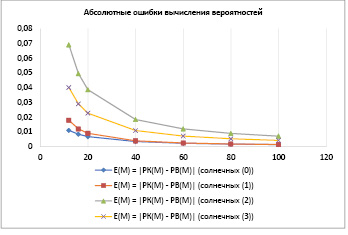
Рис. 4. Зависимость абсолютной ошибки вычисления вероятностей выбора от объёма банка для выбора N
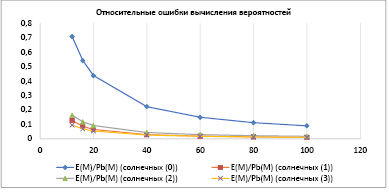
Рис. 5. Зависимость относительной ошибки вычисления вероятностей выбора от объёма банка для выбора N



