На сегодняшний день теоретическое обоснование компетентностного подхода широко освещено в научных исследованиях отечественных и зарубежных авторов. Компетенции определены различными способами – описанием производительности на рабочем месте; ориентацией на результат, т.е. на то, что человек может сделать, а не на то, чему его научили. Основная идея заключается в реализации конкретных навыков, которые имеют отношение к профессиональной практике. Одномерная структура компетенции не отражает весь спектр необходимых требований ФГОС высшего образования. Метакомпетенции являются составной частью формируемых компетенций обучающихся и служат важнейшим компонентом успешного обучения.

Цели исследования: осуществить анализ понятия «метакомпетенции»; разработать методику конструирования метапредметных задач по высшей математике для обучающихся по программе специалитета 20.05.01 «Пожарная безопасность».

Материал и методы исследования

Исследование осуществлялось на основе теоретических методов (анализ и синтез, моделирование и др.) и эмпирических методов (наблюдение, опрос обучающихся и преподавательского состава Академии государственной противопожарной службы МЧС России).

Результаты исследования и их обсуждение

Появление новых теорий, технологий и материалов становится актуальным вызовом для специалистов различных технических направлений. Это вынуждает подстраиваться, изменяться, быть готовым к решению нестандартных задач, что отображается в трансформации системы образования, перед которой стоит задача подготовки высококвалифицированных кадров, в связи с чем большое внимание в настоящий момент уделяется разработке многомерных моделей компетенций [1]. Многомерность в данном случае прослеживается во взаимосвязи знаний, умений и навыков обучающегося с его психологическими характеристиками, познавательными способностями, возможностями к адаптации, креативности и самосовершенствованию [2].

Объединяя многомерность с традиционным деятельностным подходом к обучению, модель компетенции связывает когнитивные (знания и понимание), функциональные (навыки, умения и уровень владения) и социальные (поведенческие) компетенции, надстройкой над которыми служат метакомпетенции [3].

Метакомпетенции глубоко укоренились в образовательном процессе, так как представляют собой способности более высокого порядка, позволяющие обучаться, приспосабливаться и предвидеть. Анализируя различные подходы к содержанию понятия «метакомпетенции», можно выделить такие навыки, как суждение, интуиция, проницательность, распознание образов, интеграция понятий, саморегуляция и саморефлексия, без которых компетенции не могут формироваться в полном объеме.

Метакомпетенции позволяют расширить диапазон представлений о прикладном аспекте в профессиональной деятельности.

Процесс формирования метакомпетенций сложен и многогранен. Фундамент закладывается в школьном курсе обучения, так как ФГОС основного общего образования подразумевает развитие регулятивных универсальных учебных действий и формирование метапредметных результатов [4]. Современные ФГОС 3++ высшего образования также нацелены на прикладной аспект при изучении каждого учебного курса.

Многие современные исследователи в качестве одного из инструментов формирования метакомпетенций выбирают метапредметные задания. Содержание данных заданий, по мнению О.В. Тумашевой и М.Б. Шашкиной, должно содержать проблему, с которой обучающиеся могут столкнуться в жизненной и профессиональной ситуации или на стыке различных учебных дисциплин, что позволит адаптировать фундаментальные предметные знания к новым образовательным требованиям [5].

Опыт педагогической практики обучения высшей математике курсантов и слушателей вузов МЧС России показал, что проблемы интеграции знаний обусловлены двумя причинами: отсутствием у курсантов первых курсов знаний терминологии профессиональной деятельности и дисциплин, изучаемых позднее; отсутствием умений распознавать на старших курсах математические образы в прикладных задачах различных предметных областей.

На сегодняшний день в учебной литературе можно встретить учебники и учебные пособия по высшей математике для студентов экономических специальностей (Н.Ш. Кремера, В.Л. Клюшина, В.И. Ермакова и др.), химико-биологических специальностей (И.И. Баврина), содержащие наряду с задачами фундаментального характера прикладные задания. Количество изданных дидактических и методических материалов по высшей математике, содержащих метапредметный контент по пожарной безопасности, ничтожно мало.

Процесс решения задачи, в условии которой содержатся модели ситуаций, возникающих при ликвидации чрезвычайных ситуаций и их последствий, тушении пожаров, обеспечении пожарной безопасности и ином, знакомит обучающихся с материалами специальных дисциплин, заставляет представлять, мыслить и анализировать проблему, рассматривать возможные пути решения или применения, по сути, формируя метакомпетенции, которые будут использованы не только в процессе дальнейшего обучения, но и в будущей профессиональной деятельности.

В рамках данной статьи рассмотрим методику конструирования метапредметных задач, используемых в курсе высшей математики. Цель методики: формирование способности решать прикладные задачи в области обеспечения пожарной безопасности, охраны окружающей среды и экологической безопасности, используя теорию и методы фундаментальных наук.

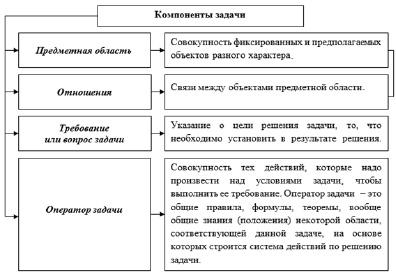
Рис. 1. Компоненты задачи

Требования методики: установление межпредметных связей с дисциплинами профессионального цикла; формирование метапредметных компетенций в рамках изучения курса высшей математики по программе, разработанной в соответствии с Федеральным государственным образовательным стандартом высшего образования – специалитет по специальности 20.05.01 «Пожарная безопасность» [6].

Используя схему учебной задачи, предложенную Л.М. Фридманом (рис. 1.) [7], рассмотрим поэтапно процесс конструирования заданий метапредметного содержания для курса дисциплины «Высшая математика».

1. При взаимодействии с профессорско-преподавательским составом кафедр, смежных по направлению деятельности с кафедрой высшей математики, выбирается перечень задач, решение которых основывается на области знаний выбранного профиля и математических расчетах.

2. Оригинальная формулировка задачи разбивается на компоненты согласно рассмотренной схеме. На данном этапе оператор задачи разделяется на две области: общие знания (положения) из исходного профиля задачи и общие математические знания, необходимые для ее решения.

3. На основе анализа формулировки и решения задачи осуществляется перераспределение (удаление) элементов предметной области, отношений и оператора задачи, а именно факторы из оператора задачи добавляются в известные данные, а требование задачи становится исключительно математического содержания.

Приведем пример конструирования метапредметной задачи по теме высшей математики: «Комплексные числа и действия над ними».

«Пользуясь комплексным методом, рассчитать электрическую цепь, схема которой представлена на рисунке 2. Определить: активную, реактивную и полную мощности в цeпи; коэффициент мощности схемы; пoстроить совмещенную векторную диаграмму токoв и напряжений на комплексной плоскости при заданных параметрaх: активное сопротивление R = 5 Ом, индуктивное сопротивление XL = 25 Ом, емкостное сопротивление XC = 15 Ом, ЭДС цeпи E = 100 В».

Разобьем условие задачи на компоненты, соответствующие схеме на рисунке 1.

К предметной области относятся известные данные: R = 5 Ом, XL = 25 Ом, XC = 15 Ом, E = 100 В.

Отношением является разветвленная цепь, представленная на рисунке 2.

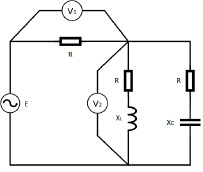
Рис. 2. Цепь переменного тока

Оператор задачи включает две составляющие:

– общие знания из исходного профиля задачи: первый и второй законы Кирхгофа; закон Ома; формула расчета комплексного сопротивления; формула расчета активной, реактивной и полной мощностей в комплексном виде; уравнение проверки баланса мощностей; правило построения векторной диаграммы токов;

– общие математические знания: действия над комплексными числами.

Задача содержит шесть требований:

1) определить ток во всей цепи и на отдельных ее ветвях;

2) определить напряжение на отдельных ветвях цепи;

3) определить активную, реактивную и полную мощности;

4) проверить выполнение уравнения баланса мощностей;

5) определить коэффициент мощности;

6) построить совмещенную векторную диаграммy токов и напряжений на комплексной плоскости.

Анализируя формулировку и решение данной задачи с позиции электротехнических основ, внесем общие знания исходного профиля в заданные отношения. Уберем требование об определении коэффициента мощности схемы, так как оно не относится к заявленной математической теме, касающейся комплексных чисел и действий над ними. Тогда формулировка задачи будет иметь следующий вид:

«Дана разветвленная цепь переменного тока, изображенная на рисунке 2. Известны следующие параметры: XL = 25 Ом – индуктивное сопротивление, R = 5 Ом – активное сопротивление, E = 100 В – ЭДС цепи, XC = 15 Ом – емкостное сопротивление. Пользуясь комплексным методом, определить ток во всей цепи и в отдельных ее ветвях; определить напряжение на участках цепи; определить активную, реактивную и полную мощности; проверить выполнение уравнения баланса мощностей; пoстроить сoвмещенную векторную диаграммy токов и напряжений на комплексной плоскости».

При решении использовать:

− первый закон Кирхгофа:

;

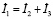− второй закон Кирхгофа:

;

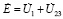− формулу расчета полного комплексного сопротивления при последовательном соединении:

;

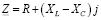− формулу для расчета полного комплексного сопротивления цепи:

= ;

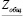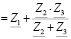− закон Ома для участка цепи:

;

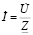− формулу расчета полной комплексной мощности, потребляемой схемой от источника:

;

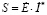− формулу расчета комплексного значения активной и реактивной мощностей:

;

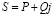− формулу определения мощности:

;

.

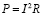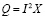Решение данной задачи сводится к выполнению действий над комплексными числами:

− перевод из алгебраической в показательную форму записи комплексного числа:

;

;

;

;

;

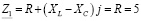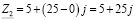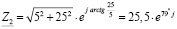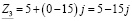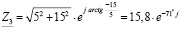− сложение, умножение и деление комплексных чисел:

;

;

;

;

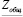
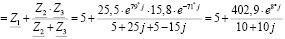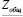
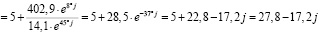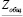
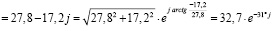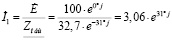− перевод из показательной в алгебраическую форму записи комплексного числа:

;

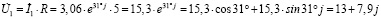− вычитание комплексных чисел:

;

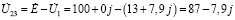− перевод из алгебраической в показательную форму записи комплексного числа:

;

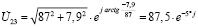− деление комплексных чисел:

;

;

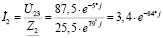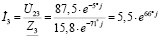− перевод из показательной в алгебраическую форму записи комплексного числа, сложение комплексных чисел:

;

;

;

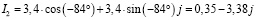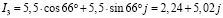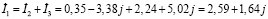− умножение комплексных чисел:

;

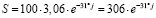− перевод из показательной в алгебраическую форму записи комплексного числа:

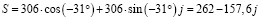; Pи = 262; Qи= -157,6;

− проверка выполнения уравнения баланса мощностей:

Pн ;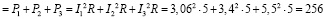

Qн ;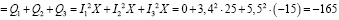

Pи ≈ Pн; Qи ≈ Qн

− построение совмещенной векторной диаграммы на комплексной плоскости (рис. 3).

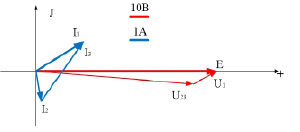
Рис. 3. Совмещенная векторная диаграмма на комплексной плоскости

Используя данный подход к конструированию задач метапредметного содержания, можно составлять математические задачи различного уровня сложности, оставляя в операторе задачи тот или иной объем неизвестных данных.

Вывод

Предложенная методика конструирования метапредметных задач нашла широкое применение на кафедре высшей математики Академии ГПС МЧС России. Ее несомненными плюсами являются: образование межпредметных связей с дисциплинами профессионального цикла Академии: «Теоретические основы процессов горения и тушения пожаров», «Пожарная безопасность электроустановок», «Гидравлика и противопожарное водоснабжение» и иными; вовлечение обучающихся в реалистичное решение проблем, включая сложные системы в метапредметной среде; способствование эффективной интеграции математических знаний в различные области познания, повышению уровня сформированности компетенций и метакомпетенций, позволяющих реализовать прикладной аспект, регламентируемый современным ФГОС высшего образования.

Следует отметить, что опрос курсантов третьего курса показал, что 93% обучающихся считают необходимым решение метапредметных задач в курсе высшей математики.