Тектонические движения, образование и развитие складчатых и разрывных структур, зон трещинноватости, зон подготовки землетрясений, формирование ряда месторождений в значительной степени обусловлены напряженно-деформированным состоянием коры. Способствующие этому процессы сжатия, растяжения земной поверхности в настоящее время активно изучаются в области решения краевых задач упругости, вязко-упругости, упруго-пластичности для выяснения динамических условий формирования месторождений полезных ископаемых. Сейчас, когда сокращается фонд перспективных положительных структур в традиционных нефтегазодобывающих районах, возникает интерес к неантиклинальным ловушкам, с которыми могут быть связаны средние и малые месторождения нефти и газа. В связи с этим использование математического моделирования напряженно-деформированного состояния пород в массиве позволяет выявить динамические ловушки, зоны растяжения, в которых при благоприятных условиях может произойти образование залежи углеводородов. Одним из применяемых в этом случае методов является метод конечных элементов.
Цель исследования – разработка алгоритма моделирования напряженно-деформированного состояния массива горных пород с помощью метода конечных элементов [1, 2] для последующего прогнозирования зон растяжения и сжатия.
Материалы и методы исследования
Метод конечных элементов в настоящее время активно используется для решения различных инженерных задач, таких как: строительство, гидро- и аэродинамика, горное дело и новейшая техника и т.д.
В данном методе реальная континуальной среда заменяется ее дискретной моделью, при этом применяются вариационные принципы, а дифференциальные уравнения представляются системой алгебраических уравнений, которая решается любым из известных численных методов.
Конечные подобласти, на которые разбивается рассматриваемая область (одно- , двух- или трехмерная), называются конечными элементами [3] (рис. 1а, 1б).
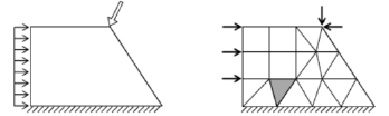
а)
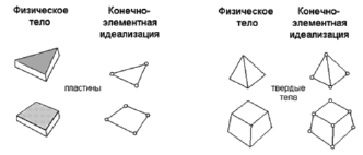
б)
Рис. 1. Разбиение области на конечные элементы
Наибольшее распространение получил метод конечных элементов в перемещениях. Главными искомыми считаются перемещения узловых точек дискретной схемы, напряжения уходят на второй план.
Приведем упрощенный вариант упруго-пластической задачи для двумерного случая. Деформация – это изменение или формы, или размеров, или объема тела. При упругих деформациях после действия на тело внешних сил изменение полностью исчезает, при пластических деформациях они сохраняются и после того, как внешние силы перестали действовать [4]. Рассмотрим часть тела, определенную двумерной областью D. Cσ – граница области, где приложены силы, Cu – граница, где тело зафиксировано в пространстве,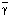 
– вектор, направленный по нормали к границе наружу, 
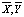– объемные силы, действующие на тело (рис. 2). При исследовании механизма деформирования блока или процесса образования разрыва при характерных размерах порядка 102 км целесообразно использовать модель пластины. Необходимо определить значения относительных деформаций εX, εY и двух нормальных и касательного напряжений σX, σY, τXY вдоль соответствующих осей. Пусть вектор 
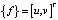– вектор перемещений рассматриваемой точки области D.
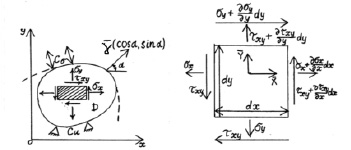
Рис. 2. Упруго-пластическая задача
При изучении кратковременных процессов в ряде случаев естественно учитывать упругие, а при изучении длительных процессов – временные, реологические свойства вещества. Рассмотрим состояние тела при произвольной нагрузке. Выпишем необходимые дифференциальные уравнения, выражающие состояния объекта, происходящие в области малых деформаций.
Уравнения равновесия
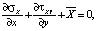
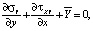(1)
где силы обусловлены, например, градиентом температуры, гравитацией и т.п.
Зависимости между деформациями и перемещениями
Условия совместности деформаций и пере- мещений называются соотношениями Коши:
,
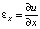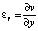, (2)
,
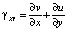γXY – деформация сдвига.
Уравнение состояния для упругих компонент – обобщенный закон Гука
Наращивание деформаций в твердых телах прямо пропорционально наращиванию напряжения:
,
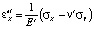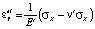, (3)
,
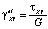где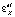 
, 
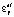– относительные деформации вдоль соответствующих осей;
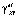– угловое перемещение;
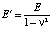– модуль Юнга;
v – коэффициент Пуассона;
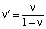– абсолютная величина отношения поперечной и продольной относительной деформации образца материала. Данный коэффициент несет информацию о природе материала, из которого изготовлен образец;
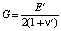– модуль сдвига.
Уравнения состояния для пластических компонент
Согласно деформационной теории пла- стичности:
,
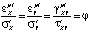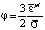, (4)
;
;
;
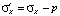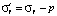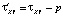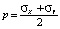– гидростатическое давление;
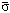– эквивалентное напряжение, 
;
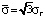σT – предел текучести при сдвиге.
Условия текучести Мизеса
Предельные значения проявления пластических свойств будут выглядеть следующим образом:
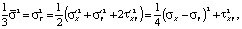(5)
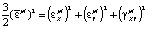. (5’)
Общая деформация
Сложение компонент пластической и упругой деформации:
,
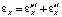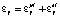, (6)
.
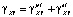Граничные условия:
А) геометрические, на Cu:
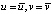; (7)
В) силовые, на Cσ:
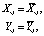(8)
где
,
.
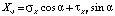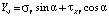Результаты исследования и их обсуждение
В двумерной области D с границей C уравнения равновесия (1) и механические граничные условия (8), (7) можно преобразовать при помощи вспомогательных условий совместности (2), (4), (5). Используем условие минимума полной потенциальной энергии системы (принцип Лагранжа). Тогда принцип виртуальной работы в приращениях будет иметь вид [5]:
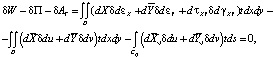(9)
где t –толщина рассматриваемой пластины;
δW – элементарная энергия деформации;
δП – элементарная потенциальная энергия;
δAT – элементарная работа приложенных сил;
ds – элемент длины на границе области;
δdu, δdv – виртуальные перемещения, удовлетворяющие (2) и нулевые на Cu.
Применим дискретизацию пространства, т.е. рассматриваемую область D разобьем на ограниченное число треугольных элементов (рис. 3) и введем допущения о распределении перемещений внутри каждого элемента.
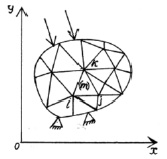
Рис. 3. Аппроксимация области конечными элементами
Имеем:
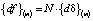– приращение перемещения в одном конечном элементе (m);
N – матрица дифференцирования функций перемещений,
,
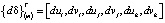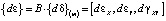, (10)
,
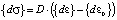B – матрица функций перемещений;
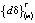– вектор узловых перемещений элемента (m);
{dε0} – начальная деформация;
D – матрица связи напряжений и дефор- маций.
Тогда принцип виртуальной работы можно выразить уравнением:
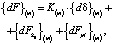(11)
где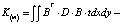 
матрица жесткости, связывающая приращения нагрузки dF с приращениями узловых перемещений:
,
.
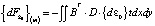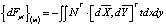Определяя зависимости (11) по всем элементам и используя условие непрерывности напряжения в узлах и условия равновесия сил, составим систему уравнений для всей конструкции. Определим решения в узлах путем решения системы линейных уравнений для заданных граничных условий, а перемещения, деформации и напряжения внутри элементов вычислим по (10) [6].
Опишем коротко алгоритм решения задачи.
1. В начале i-го шага вычисляем матрицу жесткости, входящую в (11), для упругих элементов.
2. Далее, чтобы в элементе (m) возникла текучесть, необходимо, чтобы приращение нагрузки было rm{dF}, где rm – коэффициент относительной нагрузки, при котором эквивалентное напряжение становится равным пределу текучести (выражение в правой части (5)). Этот коэффициент находится для всех упругих элементов.
3. Упругий элемент с минимальным значением rm становится элементом, текучесть которого наступает на i-м шаге.
4. Напряжения и деформации после этого шага определяются в виде:
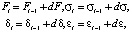
где индекс соответствует шагу приращения нагрузки.
5. Решение задачи получается путем итераций, пока не будет достигнута заданная нагрузка.
Для реализации алгоритма необходимо применять системы автоматизированного проектирования, которые используют численные методы расчета полевых и сложных инженерных задач, сводящиеся к приближенному решению дифференциальных уравнений в частных производных. Наибольшее применение получили программные продукты, использующие метод конечных элементов: Maxwell EM, ANSYS, EMS, FLUX 2D и FLUX 3D, MagNet, Magneto, FEA, ELCUT и др.
Выводы
Разработан алгоритм, позволяющий моделировать напряженно-деформированное состояние массива горных пород с помощью метода конечных элементов для двумерного случая. При этом, имея достаточный уровень геофизической изученности, при существующих признаках неотектонических движений исследуемого района возможно моделировать механизмы, сопровождающие процессы растяжения с разрывными нарушениями коры и литосферы, что позволит выявить динамические ловушки, зоны растяжения, в которых при благоприятных условиях может произойти образование залежи углеводородов.