Два последних десятилетия ведутся интенсивные научные исследования методов идентификации нелинейных динамических систем, представленных различными математическими моделями. Весьма перспективной в этом отношении является интегральная модель «вход-выход», состоящая из нескольких уравнений Вольтера, ядра которых образованы из соответствующих слагаемых ряда Вольтера [1, 2]. Один из подходов к идентификации квадратичного ядра (двумерной импульсной переходной функции (ИПФ)) [3, 4] требует вычисления смешанной производной второго порядка от двумерного выходного сигнал fкв(t, τ) идентифицируемой системы при подаче на ее вход серии прямоугольных импульсов разной амплитуды в разные моменты времени [5]. Следовательно, необходимо по измеренным в дискретные моменты времени (ti, τj) зашумленным значениям 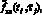
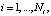
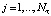 вычислить смешанную производную
вычислить смешанную производную 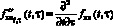 .
.
Как известно, задача дифференцирования даже функции одной переменной является некорректно поставленной задачей, когда небольшие ошибки измерения значений функции вызывают существенные ошибки в производной. В работах [6, 7] для устойчивого вычисления первой производной использовались одномерные сглаживающие кубические сплайны (СКС). При соответствующем задании краевых условий и выборе параметра сглаживания (из условия минимума СКО сглаживания) удается с приемлемой точностью построить оценку для ИПФ линейной стационарной системы. Для устойчивого вычисления смешанной производной второго порядка 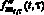 в данной работе предлагается также использоваться сглаживающий сплайн, но уже бикубический, т.е. являющийся функцией двух переменных, который будем обозначать как СБС (сглаживающий бикубический сплайн). Однако построение такого сплайна существенно сложнее построения одномерного СКС. Во-первых, краевые условия задаются уже не в двух точках, а на четырех прямых, являющихся границами прямоугольной области построения СБС. Во-вторых, из-за разной «гладкости» функции fкв(t, τ) по разным переменным t, τ необходимо выбрать уже два параметра сглаживания αt, ατ (по каждой переменной сплайна) из условия минимума СКО сглаживания. Эти два момента обусловили две основные задачи, которые решаются в данной работе:
в данной работе предлагается также использоваться сглаживающий сплайн, но уже бикубический, т.е. являющийся функцией двух переменных, который будем обозначать как СБС (сглаживающий бикубический сплайн). Однако построение такого сплайна существенно сложнее построения одномерного СКС. Во-первых, краевые условия задаются уже не в двух точках, а на четырех прямых, являющихся границами прямоугольной области построения СБС. Во-вторых, из-за разной «гладкости» функции fкв(t, τ) по разным переменным t, τ необходимо выбрать уже два параметра сглаживания αt, ατ (по каждой переменной сплайна) из условия минимума СКО сглаживания. Эти два момента обусловили две основные задачи, которые решаются в данной работе:
- разработка алгоритма, позволяющего строить сглаживающий бикубический сплайн с большим числом комбинаций краевых условий на разных границах области построения сплайна;
- выбор двух параметров сглаживания (по каждой переменной сплайна) из условия минимума СКО сглаживания на основе проверки статистических гипотез об оптимальности того или иного параметра сглаживания.
Материалы и методы исследования
Предположим, что регистрируемый в узлах прямоугольной сетки 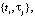
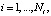
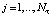 , зашумленный сигнал
, зашумленный сигнал 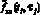 допускает представление:
допускает представление:
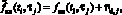
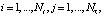 (1)
(1)
где ηi,j – случайный шум измерения с нулевым средним и дисперсией 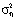 . Заметим, что узлы как ti, так и τj могут иметь не одинаковый и не равный шаг. Требуется по исходным данным
. Заметим, что узлы как ti, так и τj могут иметь не одинаковый и не равный шаг. Требуется по исходным данным 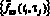 вычислить смешанные производные сглаживающего сплайна. Простой, но достаточно эффективный алгоритм вычисления частных производных СБС (при заданных параметрах сглаживания αt, ατ) можно получить, обобщая методику построения самого СБС работы [7]. Предлагаемый алгоритм вычисления частных производных СБС можно представить следующими шагами.
вычислить смешанные производные сглаживающего сплайна. Простой, но достаточно эффективный алгоритм вычисления частных производных СБС (при заданных параметрах сглаживания αt, ατ) можно получить, обобщая методику построения самого СБС работы [7]. Предлагаемый алгоритм вычисления частных производных СБС можно представить следующими шагами.
Шаг 1. Для каждого фиксированного значения аргумента τj и заданного параметра сглаживания αt строится одномерный СКС 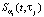 по зашумленным значениям
по зашумленным значениям 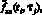
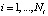 (т.е. СКС строится по переменной t). Напомним, что каждый из Nτ построенных CKC на отрезке
(т.е. СКС строится по переменной t). Напомним, что каждый из Nτ построенных CKC на отрезке 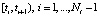 представляет собой полином третьей степени вида [8, 9]:
представляет собой полином третьей степени вида [8, 9]:
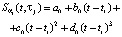 (2)
(2)
и на всем интервале 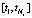 имеет вторую непрерывную производную. Так как при построении сплайна находятся коэффициенты сплайна
имеет вторую непрерывную производную. Так как при построении сплайна находятся коэффициенты сплайна 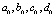 , то вычисление частной производной от сплайна
, то вычисление частной производной от сплайна 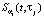 по переменной t можно осуществить по формуле
по переменной t можно осуществить по формуле
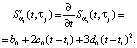 (3)
(3)
Очевидно, что при t = ti, из формулы (3) получаем
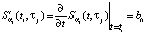 .
.
Шаг 2. Для каждого фиксированного значения аргумента ti при заданном параметре сглаживания ατ строится одномерный СКС 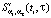 по значениям частной производной
по значениям частной производной 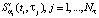 (т.е. СКС строится по переменной τ). Каждый из Nt построенных CKC на отрезке
(т.е. СКС строится по переменной τ). Каждый из Nt построенных CKC на отрезке 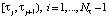 представляет собой полином третьей степени вида
представляет собой полином третьей степени вида
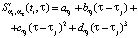 (4)
(4)
и на всем интервале 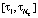 имеет вторую непрерывную производную. Для вычисления смешанной производной второго порядка выполним дифференцирование (4) по переменной τ. Получаем
имеет вторую непрерывную производную. Для вычисления смешанной производной второго порядка выполним дифференцирование (4) по переменной τ. Получаем
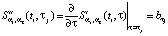 . (5)
. (5)
Таким образом, построен алгоритм вычисления смешанной производной с высокой вычислительной эффективностью – число вычислительных операций можно выразить формулой: C∙Nt∙Nτ, где C – константа, не зависящая от Nt, Nτ (для одномерного СКС значение C не превышает 60 [8]).
Напомним, что для однозначного вычисления коэффициентов одномерного СКС 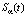 необходимо задать так называемые краевые условия на левой и правой границе отрезка (для определенности обозначим эти границы как t1 и tN), на котором строится СКС [8, 9]. Так как многие алгоритмы непараметрической идентификации используют значения производных от построенных сплайнов, то целесообразно в качестве краевых условий принимать значения первых производных, т.е. условия
необходимо задать так называемые краевые условия на левой и правой границе отрезка (для определенности обозначим эти границы как t1 и tN), на котором строится СКС [8, 9]. Так как многие алгоритмы непараметрической идентификации используют значения производных от построенных сплайнов, то целесообразно в качестве краевых условий принимать значения первых производных, т.е. условия
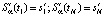 . (6)
. (6)
Алгоритм построения СКС с такими условиями был изложен в работе [7]. К сожалению, в ряде случаев информация о точных значениях 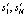 первой производной отсутствует, и в этом случае обращаются к естественным краевым условиям вида [6]:
первой производной отсутствует, и в этом случае обращаются к естественным краевым условиям вида [6]:
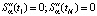 , (7)
, (7)
которые могут значительно увеличить ошибку идентификации по сравнению с условиями (6) [7]. Задание краевых условий при построении двумерного сплайна существенно усложняется из-за необходимости задавать сочетания разных типов краевых условий не в двух точках, а на четырех прямых, являющихся границами прямоугольной области, в которой строится СБС. Поэтому в разработанном пакете прикладных программ (используемого при решении практических задач идентификации) предусмотрена возможность задавать любые комбинации из краевых условий (6), (7) на этих четырех границах. Пример такого задания будет приведен ниже в описании выполненного вычислительного эксперимента.
Ранее при изложении алгоритма вычисления смешанной производной предполагалось, что параметры сглаживания αt, ατ определены. Необходимость введения двух параметров сглаживания была обусловлена разной степенью «гладкости» дифференцируемой функции по переменным t, τ, и эта разница может быть весьма значительной. Как же определить приемлемые значения (исходя из минимума ошибки дифференцирования) этих параметров? Очевидно, что нахождение значений этих параметров является более сложной задачей, чем выбор параметра сглаживания в одномерном СКС, где находится только один параметр. Для выбора двух параметров αt, ατ предлагается следующий подход, основанный на проверке статистических гипотез об оптимальности параметра сглаживания [10], который использовался в работах [6, 7] для выбора одного параметра сглаживания.
Первоначально рассмотрим выбор параметра αt. Введём статистику
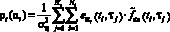 , (8)
, (8)
где 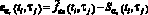 – невязка i, j-ого измерения,
– невязка i, j-ого измерения, 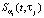 – СКС с параметром сглаживания αt, построенный по переменной t при фиксированном значении
– СКС с параметром сглаживания αt, построенный по переменной t при фиксированном значении 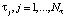 . В качестве параметра сглаживания αt принимается значение
. В качестве параметра сглаживания αt принимается значение 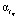 , для которого выполняется неравенство
, для которого выполняется неравенство
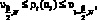 (9)
(9)
где величины 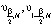 – квантили χ2-распределения с
– квантили χ2-распределения с 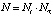 степенями свободы уровней
степенями свободы уровней 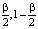 соответственно. Величина β определяет вероятность ошибки первого рода при проверке гипотезы об оптимальности (величина среднеквадратической ошибки сглаживания) оценки
соответственно. Величина β определяет вероятность ошибки первого рода при проверке гипотезы об оптимальности (величина среднеквадратической ошибки сглаживания) оценки 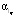 и, как правило, β = 0.05. Если N > 30, то для вычисления квантилей χ2-распределения при β = 0.05 можно использовать простые формулы
и, как правило, β = 0.05. Если N > 30, то для вычисления квантилей χ2-распределения при β = 0.05 можно использовать простые формулы
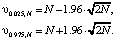 (10)
(10)
Вычисление 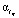 сводится к решению нелинейного уравнения
сводится к решению нелинейного уравнения
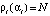 (11)
(11)
итерационными алгоритмами. В качестве 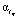 принимается очередное приближённо решение
принимается очередное приближённо решение 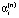 уравнения (11), которое удовлетворяет неравенству (9).
уравнения (11), которое удовлетворяет неравенству (9).
Для выбора параметра ατ введём статистику
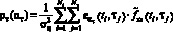 , (12)
, (12)
где 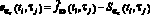 – невязка i, j-ого измерения,
– невязка i, j-ого измерения, 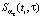 – СКС с параметром сглаживания ατ, построенный по переменной τ при фиксированном значении
– СКС с параметром сглаживания ατ, построенный по переменной τ при фиксированном значении 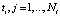 . В качестве параметра сглаживания ατ принимается значение
. В качестве параметра сглаживания ατ принимается значение 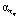 , для которого выполняется неравенство
, для которого выполняется неравенство
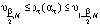 . (13)
. (13)
Эффективность предложенного подхода к выбору двух параметров сглаживания СБС будет показана ниже на результатах выполненного вычислительного эксперимента.
Результаты исследования и их обсуждение
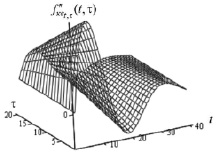
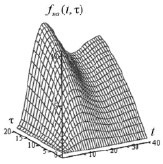
В качестве «точной» смешанной производной 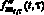 была принята функция двух аргументов, показанная на рис. 1, а. Проинтегрировав
была принята функция двух аргументов, показанная на рис. 1, а. Проинтегрировав 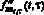 по переменным t, τ, получаем «точную» функцию fкв(t, τ), показанную на рис. 1, б. Для перехода к временным осям оцифровку осей τ1, t нужно умножить на шаг по времени 0,04, а оцифровку осей τ2, τ – на шаг 0,15 с.
по переменным t, τ, получаем «точную» функцию fкв(t, τ), показанную на рис. 1, б. Для перехода к временным осям оцифровку осей τ1, t нужно умножить на шаг по времени 0,04, а оцифровку осей τ2, τ – на шаг 0,15 с.
а) б)
Рис. 1. Точные функции 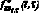 и fкв(t, τ)
и fкв(t, τ)
Зашумленные значения 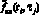 генерировались в соответствии с (1) и искажались нормально распределённым шумом с относительным уровнем 0,04, при этом
генерировались в соответствии с (1) и искажались нормально распределённым шумом с относительным уровнем 0,04, при этом 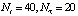 . При построении СБС в точках
. При построении СБС в точках 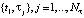 задавались краевые условия
задавались краевые условия 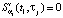 , на остальных трех границах области построения сплайна
, на остальных трех границах области построения сплайна 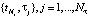 ,
, 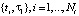 ,
, 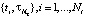 задавались вторые нулевые производные (из-за предполагаемого отсутствия априорной информации о значениях первой производной).
задавались вторые нулевые производные (из-за предполагаемого отсутствия априорной информации о значениях первой производной).
а) б)
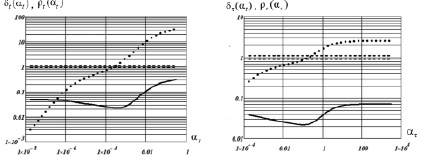
Рис. 2. Выбор параметров сглаживания 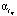 ,
, 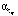
На рис. 2, а, приведены зависимости от параметра сглаживания αt: относительной ошибки сглаживания (сплошная кривая)
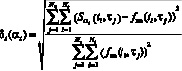 ; (14)
; (14)
статистика 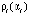 на рисунке показана точечной кривой; штрихами нанесены квантили
на рисунке показана точечной кривой; штрихами нанесены квантили 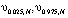 . Последние три величины для приемлемого масштаба отображения на рисунке поделены на величину
. Последние три величины для приемлемого масштаба отображения на рисунке поделены на величину 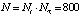 . На рис. 2, б, нанесены аналогичные характеристики
. На рис. 2, б, нанесены аналогичные характеристики 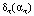 ,
, 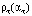 параметра сглаживания ατ сплайна
параметра сглаживания ατ сплайна 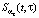 , который строится по переменной τ при фиксированных значениях ti. Как следует из (9), (13), в качестве параметров
, который строится по переменной τ при фиксированных значениях ti. Как следует из (9), (13), в качестве параметров 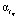 ,
, 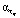 принимаются значения, для которых значения статистик
принимаются значения, для которых значения статистик 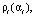
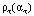 находятся между штриховыми прямыми (квантили (10)). Анализ этих графиков позволяет сделать вывод, что предложенный подход к выбору двух параметров сглаживания позволяет: а) вычислить значения
находятся между штриховыми прямыми (квантили (10)). Анализ этих графиков позволяет сделать вывод, что предложенный подход к выбору двух параметров сглаживания позволяет: а) вычислить значения 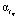 ,
, 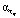 из области минимума соответствующих относительных ошибок сглаживания (рис. 2); б) определить разные
из области минимума соответствующих относительных ошибок сглаживания (рис. 2); б) определить разные 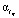 ,
, 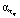 в зависимости от «гладкости» функции fкв(t, τ) по переменным t, τ. Принятая в эксперименте функция fкв(t, τ) по переменной τ более гладкая, и поэтому значение
в зависимости от «гладкости» функции fкв(t, τ) по переменным t, τ. Принятая в эксперименте функция fкв(t, τ) по переменной τ более гладкая, и поэтому значение 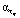 примерно на два порядка больше
примерно на два порядка больше 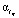 и это уменьшает ошибку дифференцирования по этой переменной. Относительная ошибка вычисленной
и это уменьшает ошибку дифференцирования по этой переменной. Относительная ошибка вычисленной 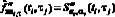 составила 0,127. Для сравнения была определена наименьшая относительная ошибка вычисления смешанной производной равная 0,109 (в вычислительном эксперименте это можно осуществить), что позволяет сделать вывод о приемлемой для практики точности вычисления смешанной производной второго порядка по зашумленным данным. Для относительного уровня шума 0,10 эти ошибки составили 0,205 и 0,188 соответственно. Это позволяет делать вывод о хорошей устойчивости алгоритма к шумам измерения исходных данных.
составила 0,127. Для сравнения была определена наименьшая относительная ошибка вычисления смешанной производной равная 0,109 (в вычислительном эксперименте это можно осуществить), что позволяет сделать вывод о приемлемой для практики точности вычисления смешанной производной второго порядка по зашумленным данным. Для относительного уровня шума 0,10 эти ошибки составили 0,205 и 0,188 соответственно. Это позволяет делать вывод о хорошей устойчивости алгоритма к шумам измерения исходных данных.
Заключение
Предложенный подход позволяет с приемлемой точностью вычислить смешанную производную второго порядка, дает возможность задавать разные типы краевых условий (исходя из имеющейся априорной информации), а также учитывать (за счет выбора двух параметров сглаживания) разную гладкость дифференцируемой функции по отдельным переменным. Алгоритм дифференцирования на основе сглаживающего бикубического сплайна может работать с различными шагами дискретизации, как по каждой переменной, так и с разным шагом дискретизации «внутри» каждой переменной, что особенно ценно при обработке реальных экспериментальных данных.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 20-38-90041.



