Проблема повышения качества обучения постоянно находится в центре внимания отечественного и зарубежного образования. Болонская декларация, принятая в 1999 г., определила стратегию высшего образования, сформулировав основные задачи, которые включают разработку методологии модульного построения образовательных программ высшего профессионального образования. Для преподавателя эта система позволила рационально планировать учебный процесс по дисциплине, контролировать ход усвоения изучаемого материала, своевременно вносить коррективы в организацию учебного процесса по результатам текущего рейтингового контроля, оценивать выполнение каждого учебного поручения, объективно определять оценку по предмету, позволяя рассматривать контроль как неотъемлемую часть образовательного процесса [1]. При проектировании рабочих программ дисциплин и учебных предметов для организации обучения студентов в вузе преподаватели используют уже не только традиционные режимы организации аудиторной и самостоятельной работы студентов, но и постоянно стараются находить новые формы, обеспечивающие повышение качества обучения. Здесь, в частности, присутствуют различные формы анализа и систематизации по группам допускаемых студентами ошибок, с целью дальнейшей работы над методикой их устранения [2]; разработка новых критериев и функций оценивания, влекущих за собой изменения системы мониторинга качества обучения [3], и другие работы, позволяющие системе стать более эффективной в тех случаях, когда такая работа носит систематический и целенаправленный характер.
Цель данной работы – описать и ознакомить читателей с методикой, позволяющей оперативно осуществлять проведение в группе объективного индивидуального контроля знаний студентов по различным разделам дисциплины, а также совокупную оценку по всем разделам. Данная методика, разработанная и апробированная авторами как в аудиторном, так и в режиме онлайн, охватывает полный цикл проведения рейтингового контроля усвоения материала: оперативную подготовку индивидуальных тестов каждому студенту; автоматическое объективное (фактически без личного участия преподавателя) тестирование с определением индивидуальных рейтинговых оценок степени усвоения; выявление наиболее трудноусвояемых разделов тематических заданий. Регулярное проведение на занятиях подобного тестирования позволяет получить предварительную достоверную оценку степени усвоения изучаемой дисциплины, которую можно использовать при аттестации.
Материалы и методы исследования
Формирование тестовых заданий и проведение процедуры тестирования по различным дисциплинам должно соответствовать требованиям Федеральных государственных образовательных стандартов высшего образования. Материалы, входящие в содержание тестовых вопросов, не должны выходить за рамки утвержденных рабочих программ дисциплин.
Критерии оценивания учебной деятельности студента должны отвечать, в частности, следующим принципам [3]:
– оценка должна быть валидной, то есть результат должен быть четко и ясно определен;
– процедура оценивания должна быть ясной и четкой;
– должен иметься механизм апелляции и повторного оценивания, оценка должна быть прозрачна и понятна студентам;
– надежность оценки – это ее устойчивость, что в свою очередь подтверждается на сходном материале в подобных условиях;
– необходимы унификация временных отрезков и условий контроля, одинаковые временные критерии для однотипных заданий, а также одинаковые методы контроля;
– регистрация результатов всегда должна быть систематизирована.
Результаты исследования и их обсуждение
Процедура проведения рейтингового контроля знаний по дисциплинам включает в себя следующие этапы: подготовку вопросов для включения их в индивидуальные тестовые задания; оперативное индивидуальное тестирование студентов с выставлением рейтинговых оценок; проведение анализа наиболее трудноусвояемого материала. Первый тип тестов состоит из обычных текстовых вопросов-утверждений с возможным дополнением их рисунком, схемой, графиком, формулой. Студент просто определяет, верен ли этот вопрос-утверждение или неверен. Кратко обозначим верный вопрос «1», а неверный «0», или «вопрос верный» и «неверный». Уровень сложности подобных утверждений формируется преподавателем в соответствии с рабочей программой дисциплины (РПД) таким образом, чтобы правильный ответ (верное утверждение) продемонстрировал квалификацию и уровень знаний студентов. Например, для раздела «Трёхфазные цепи в электротехнике» в РПД Электротехника относительно высокий уровень оценки знаний может быть отражен в следующем вопросе-утверждении (далее просто «вопрос»): «В 3-фазной симметричной цепи звезда-звезда с нулевым проводом частота переменного тока, текущего по нулевому проводу, имеет ту же частоту, что и фазный ток потребителя». Этот вопрос предполагает не поверхностное знание предмета, а более углубленное. Потому, что если бы цепь была несимметричной, то правильный ответ на этот вопрос был бы «да», обозначим «1». Но если цепь симметрична, как сказано в вопросе, то правильным ответом будет «0», потому что в этом случае ток в нулевом проводе не будет переменным с частотой фазного тока, он постоянно будет равен 0. Естественно, чем больше число N подобных различных вопросов будет включено в тест, тем точность оценки рейтингового уровня знаний студентов по какому-то разделу дисциплины будет выше. Как показывает практика, для достоверной оперативной (5–10 мин) проверки достаточно ограничить значение вопросов в тесте N, например 6. При появлении же каких-то сомнений в оценке или для более глубокой проверки достаточно просто повторить тест, естественно, уже с другими вопросами. По результатам ответов на все шесть вопросов каждому студенту системой выставляется итоговая рейтинговая оценка от 0 до 1. Важно отметить, что число «верных» и «неверных» вопросов в тестах не зафиксировано и произвольно формируется системой. Потому что если число правильных ответов в тесте предопределено, то экзаменуемый будет стараться подогнать свой ответ под правильный результат. Поэтому число «верных» вопросов в каждом тесте может быть любым в пределах заданного преподавателем интервала. Например, от 1 до 5 или от 2 до 4. Естественно, в тесте должен быть хотя бы один «верный» вопрос. Далее возникает вопрос, каким же образом в системе по результатам ответов на все N вопросов следует формировать относительную рейтинговую оценку Q в пределах от 0 до 1. Очевидно, что если единицей отмечается верный вопрос, то рейтинговая оценка Q по тесту должна повышаться, а если единицей отмечается неверный вопрос, то рейтинговая оценка Q должна понижаться. Насколько должна повышаться или уменьшаться – зависит от относительной цены вопроса Ci в данном i-м тесте. Обозначим через m1i – количество верных вопросов в i-м тесте. Причем соблюдаем условие, что 1 ≤ m1i < N. Тогда относительная цена вопроса в этом тесте определится следующим образом: Ci = 1/m1i.
Обозначим через n1i – число вопросов в тесте, которые студент отметил как верные. Естественно, при этом возможны случаи, когда единицей отмечены как верные вопросы, их число обозначим a1i, так и неверные b1i. Причем соблюдается условие: a1i + b1i = n1i. В случае если студент обозначил единицами только верные вопросы, т.е. a1i = n1i, рейтинговая оценка определяется пропорционально относительному числу отмеченных вопросов: Qi = Ci*(n1i/m1i). То есть каждый отмеченный единицей верный вопрос увеличивает рейтинговую оценку Q на цену вопроса. Действительно, если m1i = 1, то цена вопроса в тесте Ci = 1/m1i = 1, если m1i = 5, то Ci = 1/5 = 0,2. В случае если единицей отмечены как верные, так и неверные вопросы, то должно соблюдаться правило: каждая единица в первом случае должна повышать, а во втором случае понижать рейтинговую оценку на относительную цену вопроса. Окончательно формирование рейтинговой оценки осуществляется по правилу:
Qi = Ci*(a1i/m1i) – Ci*(b1i/m1i) =
= Ci*(a1i – b1i)/m1i.
В случаях, когда a1i < b1i, понижение рейтинговой оценки, естественно, происходит только до 0.
В итоге, например, если в тесте присутствуют четыре правильных вопроса, то студент, отметив единицами из них только два, получает рейтинговую оценку 0,5, что справедливо. Но если при этом студент отметит единицей ещё и неверный вопрос, то рейтинговая оценка понизится до 0,25. Это правило делает более ответственным и обоснованным выбор студентом правильных вопросов. Подобное оценивание, когда за каждый правильный ответ рейтинговая оценка увеличивается, а за каждый неправильный – уменьшается, приводит к более точной оценке реальных знаний испытуемых. На практике студенты, получив свои тесты (билеты или онлайн), при необходимости сопровождаемые схемой, графиком или рисунком, в течение 5–10 мин определяют и отмечают единицей верные вопросы, а неверные просто оставляют пустыми. Для сокращения времени занесения результатов в таблицу студенты в поле Ответ1 (первый тест) или Ответ2 (второй тест) записывают просто десятичное число, равное по значению 6-разрядному двоичному, в котором наличие 1 в соответствующих разрядах (р1-р6) указывает на правильность этого ответа (рис. 1).


а) б)
Рис. 1. Таблицы рейтинговых оценок тестов с шестью вопросами: а) идеальная; б) реальная
Двоичное число, наглядно показывающее студенту, какие из вопросов у него отмечены единицами верными, формируется автоматически системой. Итоги рейтинговой оценки становятся доступны студентам по завершению тестирования.
Естественно, проведение контроля уровня знаний с выставлением рейтинговых оценок целесообразно проводить не только в случаях, когда студентам предлагаются тестовые вопросы-утверждения, но также и тогда, когда необходима проверка знаний и умения проводить различные расчеты и вычисления. Например, расчет токов в цепях или расчет параметров элементов в схемах. Выполнение таких заданий тестов требует определенного времени для их выполнения. Поэтому подобные тесты, как правило, задаются студентам уже во внеурочное время, в том числе дистанционно. Для контроля их выполнения используется Второй тип тестов. Для их проверки в системе используется другой алгоритм, позволяющий проводить проверку всех результатов с заданной для каждого из расчетов относительной погрешностью в процентах (рис. 2). Здесь также выставляется рейтинговая оценка, учитывающая, правильно ли выполнены все расчеты. Число рассчитываемых параметров в каждом тесте может достигать 10.
Разработка вопросов для подобных тестов, естественно, вызывает увеличение нагрузки преподавателя за счёт дополнительной работы по структурированию содержания дисциплины. Однако такая работа позволяет усовершенствовать учебный процесс, сосредоточиться на творческой части преподавания и экономит время при контроле.
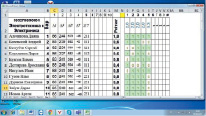
Рис. 2. Тесты с вычислениями параметров
Выше уже отмечалось, что процедура оце- нивания должна быть ясной и четкой. Здесь необходимо добавить еще и то, что оценка должна максимально отражать истинные знания студентов. С пониманием этого разрабатываются и используются соответствующие методы оценивания, отличающиеся друг от друга степенью соответствия условиям и законам окружающего мира. Наиболее часто для этого используются инструменты, разработанные в рамках научного направления «квалиметрия» [4]. В рамках такого подхода каждому вопросу присваивается свой коэффициент сложности и отпадает необходимость при контроле обучающегося подбирать близкие по сложности вопросы. Подобный квалиметрический подход и был использован в описанной выше системе тестирования для определения рейтинговой оценки по результатам выполнения одного теста. Система позволяет оценивать знания студентов по разделам дисциплины быстро, не составляя никаких проблем и студентам, и преподавателю.
Обратим внимание на то, что в описанной выше системе предусматривались ответы в двузначной логике (0 или 1), что не вполне соответствует реальным знаниям студента (ответ может быть полностью правильным, совсем неправильным, не совсем правильным и т.д.). Иными словами, система тестирования оперирует двузначными исходными данными, а результат (рейтинговая оценка) выдает в рамках непрерывнозначной шкалы от 0 до 1.
Отметим, что средневзвешенная оценка (квалиметрическая) обладает существенным недостатком. Дело в том, что рассчитанная рейтинговая оценка будет равна 0 только в том случае, когда оценки по каждому вопросу равны 0. Это объясняется свойством аддитивности расчетной формулы. Очевидно, что такая особенность не даёт возможности считать полученную оценку адекватной реальной жизненной ситуации, когда всегда существуют такие ключевые оцениваемые показатели, нулевая оценка которых приводит к нулевой оценке всего теста. Этот недостаток в некоторой степени может быть нивелирован назначением соответствующих относительных цен вопросов теста. Тем не менее такой прием не может полностью избавить методику от указанного недостатка и не позволяет отказаться от поиска более объективной и адекватной реальному миру системы оценивания.
Избавление системы тестирования от отмеченного недостатка обеспечивается применением новых методов в рамках непрерывнозначной логики, когда итоговая оценка рассчитывается с использованием специальных операторов (связок), позволяющих устранить негативное влияние свойства аддитивности. При этом можно отказаться и от представления исходных данных по непрерывнозначной шкале (например, от 0 до 1), что дает дополнительное преимущество такого подхода. Особенности такого подхода использованы в данной системе на этапе определения оценки степени усвоения по всем разделам дисциплины на основе рассчитанных выше рейтинговых оценок по результатам тестирования по отдельным тестам.
В последние десятилетия на практике все чаще применяются математические методы, основанные на применении новых непрерывнозначных логик, позволяющих совершенствовать системы оценивания различных объектов. Одной из таких логик является предложенная в 1990-х гг. канд. физ.-мат. наук Я.Я. Голотой и пока еще не получившая достойного признания логика противоположностей (логика антонимов). Для примера приведем ряд публикаций последних лет, в которых представлены различные случаи успешного применения логики противоположностей [5, 6].
В основу аксиоматики логики противоположностей положены две аксиомы, определяющие характер связей между двумя рассматриваемыми (оцениваемыми) объектами [7]:
- тесная связь γ между элементами оцениваемой системы подразумевает следующее: если характеристика хотя бы одного из элементов выходит за допустимые пределы, то и совокупная характеристика всей системы выходит из допустимых границ;
- слабая связь β между элементами означает, что выход за пределы значений, характеризующих любой из элементов, не влечет за собой вывод из допустимых границ характеристики всей системы, а лишь ухудшает ее.
Автор логики противоположностей, введя в оборот новые виды операторов (связей) γ и β, предложил и расчетные формулы для использования. Для определения суммарного рейтинга оценивания Q[C] они будут выглядеть следующим образом:
Q[C] = Q[A] + Q[B] + …+ Q[К] – при слабой связи между А, B,…K;
Q[C] = -log2[1 – (1 – 2Q[A])∙(1 – 2Q[B])∙…∙(1 2Q[K])] – при тесной связи между А, В,...K.
В приведенных формулах Q[С] – оценка сложной системы С, например совокупности тестов по всем разделам (А, В,…К) дисциплины, состоящей из элементов – тестов по разделам. Выражения Q[A], Q[B], …Q[К] – оценки элементов (тестов) А, В,…К. Каждой из оценок Q[A], Q[B], …Q[К] присваиваются весовые коэффициенты (по усмотрению преподавателя), которые не указаны, чтобы излишне не загромождать формулы. Нетрудно заметить, что если при тесной связи любая из оценок Q[A], Q[B], … Q[К] принимает значение 0, то оценка системы (в нашем случае – интегральная оценка освоения всей дисциплины по результатам тестирования) также станет равна 0, что отличает её от средневзвешенной оценки. Интегральная оценка освоения всей дисциплины получается как функция от оценок результатов отдельных тестов по разделам: Qинт = F{Q[A], Q[B],…Q[K]}.
Вид функции определяется путем указания характера связей между результатами выполнения тестов, в результате чего с использованием приведенных выше расчетных формул, при слабой или тесной связи, получается итоговое аналитическое выражение. Таким образом, использование логики противоположностей дает возможность получить в необходимых случаях оценку по результатам тестирования более объективную и адекватную реальным условиям. Кажущаяся, на первый взгляд, сложность вычислений согласно приведенным выражениям легко преодолевается разработкой программы вычислений и не составляет никаких препятствий на практике.
При определении содержания тестовых вопросов и заданий, естественно, следует уделять особое внимание формулированию предметных инновационных и актуальных технических задач, проблем, требующих вовлечения студентов в генерирование, анализ, оценку и реализацию идей, характерных для профессиональной инженерной деятельности (конструирование, моделирование и анализ ситуаций, решение практических задач).
Заключение
Рассмотренная методика оценки качества усвоения знаний у студентов, при наличии подготовленной базы сформулированных тестовых заданий (вопросов) и разработанного программного сопровождения, обеспечивает оперативное индивидуальное тестирование с выставлением рейтинговых оценок каждому студенту как по отдельным разделам дисциплины, так и по дисциплине в целом. Применение рейтинговой системы оценивания позволяет добиться более ритмичной работы студента в течение семестра, а также стимулирует их заинтересованность и творческую активность. Полученные в течение семестра рейтинговые оценки позволяют преподавателю предварительно оценить уровень полученных студентом знаний по данному предмету и в совокупности с другими факторами обоснованно выставлять соответствующие оценки.
В системе реализована возможность, по результатам тестирования выявлять наиболее трудные или недостаточно изученные разделы дисциплины, которым следует уделить в дальнейшем больше внимания. В случаях, когда возникает необходимость проведения углубленной оценки, учитывающей знание нескольких предметов или другие факторы, имеющие ключевое значение (инновационность, перспективность, экономическую целесообразность), формирование рейтингового оценивания целесообразно осуществлять с применением новых непрерывнозначных логик противоположностей (антонимов). Регулярное проведение подобного контроля с одинаковыми условиями для всех участников, оперативность и формальное устранение преподавателя от процесса оценивания результатов нацеливают студентов на качественное улучшение изучения дисциплины и стимулируют активность. Применение современных математических методов нечеткой логики противоположностей и полная автоматизация процесса тестирования позволяют рассчитывать на оперативную и максимально адекватную оценку степени усвоения студентами дисциплины. Авторы готовы ознакомить заинтересованных лиц с результатами своей работы и наработанным программным обеспечением.



