При переключении режимов работы современного оборудования возникает необходимость реализации последовательности различных задач управления. Системы с фиксированной структурой, настраиваемые обычно на установившийся режим, не обеспечивают наилучшего качества управления в других режимах. Для оптимизации режимов работы системы по выбранному критерию (быстродействие, отсутствие перерегулирования и др.) в каждом из режимов работы системы при ограничении на управляющее воздействие следует использовать перестраиваемую структуру системы управления с реализацией локальных алгоритмов управления. Повышение требований к качеству САУ техническими и технологическими объектами обуславливает необходимость решения задачи синтеза систем управления с учетом многорежимности их функционирования в априори неопределенных условиях. Многорежимность и неопределенность условий функционирования обуславливают необходимость решения проблемы синтеза многорежимных систем управления, основанных на интеллектуальных подходах. Универсальных методов решения задач синтеза многорежимных систем управления на основе интеллектуальных подходов в настоящее время не получено. Поэтому задача разработки и исследования многорежимных систем управления объектами различного назначения, анализ возможностей аппаратных и программных средств их реализации являются актуальными.
Целью исследования являлся анализ возможностей аппаратных и программных средств для разработки и исследования многорежимной системы управления на основе комбинирования регулятора с нечеткой логикой и нелинейного регулятора с аппроксимирующим управлением.
Анализ особенностей промышленных объектов управления в условиях многорежимности их функционирования
Применение многорежимных систем управления (МСУ) оправдано, когда динамический объект характеризуется следующими особенностями:
– необходимость последовательности осуществления пусковых и установившихся режимов функционирования;
– неконтролируемое воздействие внешних факторов на управляемые объекты, проявляющихся в условиях неопределенности функционирования оборудования;
– ограниченный уровень управляющего воздействия и недопустимость смены его знака (например, наличие в системе охлаждения только хладагента и отсутствие теплоагента при выводе реактора на оптимальный температурный режим), а также чрезмерное снижение его (например, уменьшение расхода подаваемого воздуха на аэрацию из-за возможного лимитирования кислорода в биореакторах);
– последовательное осуществление после пускового режима режимов стабилизации и программного управления.
Наиболее полно все перечисленные особенности проявляются, например, при управлении базовыми объектами биотехнологических производств, объектами энергетики, подвижными объектами. С учетом вышеперечисленного можно сформулировать требования к многорежимным системам управления:
– алгоритмы управления должны обеспечивать максимальное быстродействие в переходных (пусковых) режимах либо заданную точность скорости изменения управляемого параметра в пусковом режиме и не допускать значительное перерегулирование на этапе перехода к установившемуся режиму;
– регулятор (алгоритм управления) должен быть реализован как регулятор (алгоритм управления) с переключаемой структурой с помощью совмещенных как минимум двух регуляторов, один из которых релейный (либо квазирелейный с аппроксимирующим управлением [1]), а второй линейный с ограничением смены знака управляющего воздействия;
– многорежимный цифровой регулятор (МЦР) может быть использован как супервизорный регулятор в автоматизированной системе управления технологическим процессом (АСУ ТП).
Многообразие систем управления при любом варианте их реализации требует многомодульного аппаратного и программного обеспечения (ПО) для организации и проведения процесса управления и моделирования в диалоговом режиме [2]. На практике для реализации алгоритмов управления МСУ на базе интеллектуальной технологии, например на основе нечеткой логики, возможно использование нечетких алгоритмов с помощью нечетких контроллеров. Это обеспечивает существенное повышение быстродействия регуляторов с нечеткой логикой. Известен ряд поколений нечетких контроллеров [3]. К первым относятся контроллеры на основе аналоговых больших интегральных схем (Fuzzy Chips), представленных на рынке в 1987 г. В последующем (1990 г.) появились нечеткие регуляторы на основе сверхбольших интегральных схем (СБИС), интегрирующих в себе аналоговые и цифровые принципы работы. Примерами таких СБИС являются OMRON FP-3000, TOGAI-Infra Logic F 110. Впоследствии (1992 г.) разработанные нечеткие компьютеры (Fuzzy-Computers) или нечеткие процессоры (Fuzzy-Processors) повысили удобство реализации диалогового режима взаимодействия оператора и ЭВМ, а также обеспечили повышение скорости обработки поступающей информации.
Совместной разработкой фирм «Siemens» и «Inform» является процессор с нечеткой логикой FUZZY-166 на базе 16-разрядного микропроцессора фирмы «Inform». Реализация регулятора с нечеткой логикой возможна также на базе контроллера Siemens S7-300. Японская фирма «Omron» разработала для ПЛК нечеткий микропроцессор [4]. Корпорацией Klockner-Moeller (Австрия) был разработан сᴨециализированный ПЛК, сочетающий в себе fuzzy-логику и стандартные алгоритмы управления.
С введением в 1997 г. в действие ГОСТ Р МЭК 61131-7-2017 «Контроллеры программируемые. Часть 7. Программирование нечеткого управления», идентичного международному стандарту МЭК 61131-7:2000 «Контроллеры программируемые. Часть 7. Программирование нечеткого управления» (IEC 61131-7:2000 «Programmable controllers – Part 7: Fuzzy control programming», IDT), производители микропроцессорных контроллеров широко интегрируют «нечеткие» элементы в АСУТП.
Разработка МСУ предполагает компьютерное моделирование. В настоящее время среди программ для разработки МСУ применимы следующие программы и программные продукты [2]:
– программа MexBIOS Development Studio для разработки и моделирования ПО систем управления технологическими процессами и микроконтроллерами STM32F10x, STM32F4XX;
– программные продукты «Standard PID Control» и «Modular PID Control», предназначенные для конфигурирования программируемых логических контроллеров (ПЛК) SIMATIC S7, а также «PID Self Tuner», позволяющий осуществлять автонастройку для систем с ПИД-регуляторами;
– пакет Matlab со средой моделирования Simulink и fuzzyTECH, предназначенный для имитационного моделирования динамических систем, включая нечеткое моделирование [5];
– программа VisSim («Visual Solution»), позволяющая осуществлять моделирование и проектирование систем управления и цифровую обработку сигналов;
– пакет компьютерного моделирования динамических технических систем SimInTech [6], предназначенный для создания и эксплуатации автоматических систем регулирования. Отличительной особенностью программного обеспечения данного пакета является наличие программных средств моделирования систем с нечеткой логикой и нейросетевых систем.
Таким образом, разработчикам современных систем управления в настоящее время доступен широкий инструментарий реализации нечетких алгоритмов управления.
Результаты исследования и их обсуждение
Рассмотрим применение нечеткого контроллера в многорежимной системе управления подачей воздуха на аэрацию с помощью растворенного в жидкости кислорода (рО2) в биореакторе периодического действия. Реализуем уравнение закона управления МСУ в следующем виде [7]:
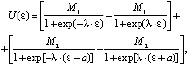(1)
где М1, М2 – коэффициенты для регулирующего воздействия соответственно на участке с зоной нечувствительности (ЗН) и за ее пределами; ε – ошибка регулирования; λ – коэффициент усиления нелинейности; 2а – величина ЗН.
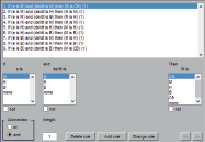
Для проектирования системы воспользуемся инструментарием нечеткой логики Fuzzy Logic Toolbox, входящим в пакет программ MatLab [5]. Для входных лингвистических переменных НР ошибки регулирования и ее производной используем следующие термы: М – малое, Н – норма, В – высокое. Для выходной лингвистической переменной НР используем следующие термы: СМ – сильно уменьшить, М – уменьшить, Н – норма, В – увеличить, СВ – сильно увеличить. База нечетких правил для определения коррекции расхода воздуха по содержанию концентрации растворенного в жидкости кислорода рО2 с использованием приведенных термов приведена в таблице.
База правил определения коррекции расхода аэрирующего воздуха в биореактор
|
Ошибка εрО2 |
Производная ошибки dεрО2/dt |
||
|
М |
СМ |
М |
Н |
|
Н |
М |
Н |
В |
|
В |
Н |
В |
СВ |
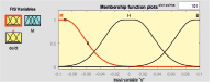
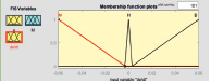
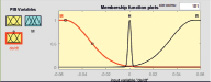
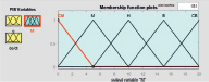
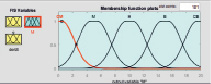
Важную роль в процессе синтеза НР играет выбор функции принадлежности (ФП). Поэтому при синтезе НР предварительно проведен анализ использования фаззификации треугольными и гауссовыми функциями принадлежности. Ошибка обучения нейро-нечеткой сети, полученная при различных ФП и разном числе эпох, показала, что при наименьшем числе эпох, равном 34, ошибка при треугольной ФП равна 0,075882; при числе эпох, равном 140, ошибка при двухсторонней гауссовской ФП наименьшая и равна 0,003283. Функции принадлежности значений переменных НР соответствующим термам для заданных диапазонов их изменения представлены на рис. 1. Результаты синтеза алгоритма построения нечеткого регулятора представлены на рис. 1.
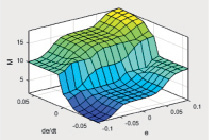
Как показал анализ поверхностей вывода регулирующего воздействия нечеткого регулятора от входных переменных, результаты с обеими ФП идентичны (рис. 1, з). Поэтому синтез НР осуществлен с использованием наиболее простых треугольных функций принадлежности и алгоритма Мамдани [8]. Дефаззификация переменных произведена с помощью метода центра тяжести [5].
а) б)
в) г)
д) е)
ж) з)
Рис. 1. Результаты синтеза алгоритма НР с треугольными (а, в, д) и гауссовыми двухсторонними (б, г, е) функциями принадлежности
При исследовании свойств системы использован интервальный подход в условиях неопределенности [9]. Согласно этому подходу рациональной моделью объекта управления по каналу регулирования рО2 в биореакторе является передаточная функция, параметры которой записываются границами интервалов их изменения и представлены в следующем виде
W(p) = Коб∙ехр(–τp)/(T22∙p2 + T1∙p + 1) =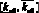 
∙ехр(–
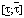p)/(
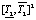∙p2 +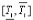 
∙p + 1), (2)
где Коб – коэффициент передачи, 0,029 ≤ kоб ≤ 0,375, %/м3/ч; Т1,Т2 – постоянные времени 10,19 ≤ T1 ≤ 14,8 мин; 41,49 ≤ Т22 ≤ 101,53 мин2; τ – время запаздывания 2,7 ≤ τ ≤ 7,5 мин.
На рис. 2 представлены переходные процессы в двухрежимной САУ с нелинейным регулятором (1) при скачкообразном действии задания на входе регулятора (кривые 1–6) и одновременном действии задания и возмущения на входе объекта в пусковом режиме (кривая 7). Причем параметры моделируемого объекта в системе с переходными процессами 1–7 соответствовали различному их сочетанию из интервалов неопределенности. В ходе экспериментов получены следующие значения параметров настройки регулятора (1): M1 = 7, M2 = 14, λ = 0,25, a = 0,1. Как видно из рис. 2, система сохраняет устойчивость, но не устраняет колебания в режиме стабилизации: амплитуда автоколебаний при действии возмущения на входе объекта в пусковом режиме составляет более 10 % задания.
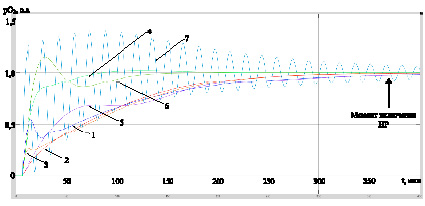
Рис. 2. Переходные процессы в САУ с нелинейным регулятором при вариабельности параметров объекта управления (кривые 1–6) и действии возмущения на входе объекта в пусковом режиме (кривая 7)
Далее рассмотрено устранение колебаний регулируемой переменной в установившемся режиме с помощью НР [8]. При исследовании систем управления в условиях параметрической неопределенности целесообразно объект управления моделировать номинальной моделью с параметрами со среднеинтервальными значениями [10]. С учетом этого параметры номинальной модели объекта были заданы в виде
=
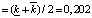[ %/м3/ч];
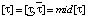
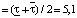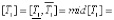
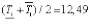мин;
= 
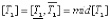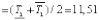мин;
=
мин,
где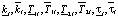 
– нижнее и верхнее значения коэффициента передачи объекта ki, постоянных времени Т1i, Т2i и времени запаздывания объекта τi соответственно; mid[νi] – середина интервального параметра [νi], i = 1,…, N.
С использованием среднеинтервальных параметров объекта осуществлена настройка нечеткого регулятора для установившегося режима. Переходный процесс в САУ с нечетким регулятором представлен на рис. 3. Из графика переходного процесса видно, что максимальная динамическая ошибка значительно уменьшилась, а недопустимые колебания полностью устранены и время их устранения не превышает времени переходных процессов 1–6 на рис. 2.
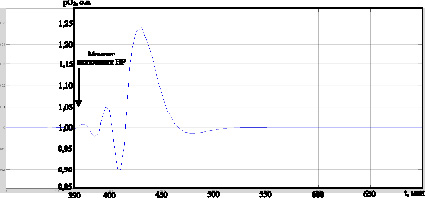
Рис. 3. Кривая переходного процесса в САУ при включении НР в установившемся режиме
Таким образом, рассмотренную систему с нелинейным аппроксимирующим регулятором нет необходимости настраивать отдельно для переходного и установившегося режимов, что в условиях неопределенности параметров динамических характеристик объекта управления и при непредсказуемом действии возмущения затруднительно. Достаточно после пускового режима включать нечеткий регулятор. Реализуемая система управления с переключением регуляторов более устойчива и нечувствительна к параметрическим и внешним возмущениям на объект по сравнению с системой с одним аппроксимирующим регулятором.
Заключение
При проектировании САУ необходимо учитывать то, что для многих промышленных объектов отсутствуют точные математические модели и для них характерны многорежимность, чрезмерная сложность, запаздывание и нелинейность. Для систем с неполной информацией, а также при высокой сложности объекта управления необходимо применение интеллектуальных САУ и, как рациональный их вариант, – комбинация переключаемых структур на основе принципов аппроксимирующего и нечеткого регулирования. Рациональное решение может быть достигнуто при системном подходе к управлению, предусматривающем решение задачи выбора структуры системы управления с учетом всех режимов работы объекта. В результате этого возникает задача разработки многорежимной системы управления, решение которой потребовало в данном случае комбинации принципов аппроксимирующего и нечеткого регулирования и, как следствие, нового алгоритма управления.
Анализ возможностей аппаратного и программного инструментария для разработки комбинированных алгоритмов управления в МСУ показывает, что, несмотря на отмеченные достоинства, они не содержат готового инструментария для конструирования алгоритмов регулирования в многорежимных системах управления c переключаемой структурой, но дают возможность их построения и моделирования. На примере двухрежимной САУ показано эффективное управление на основе комбинации аппроксимирующего и нечеткого регулятора с минимальной базой правил. Исследования многорежимной САУ процессом аэрации с помощью растворенного в реакторе кислорода проведены с использованием отечественного программного инструментария Matlab со средой моделирования Simulink и fuzzyTECH. Следовательно, актуальная задача разработки и исследования многорежимных систем управления объектами различного назначения может быть эффективно решена.