В последние годы наблюдается повышенный интерес к применению низкоорбитальных систем спутниковой связи (ССС). Такие системы нашли применение при освоении Северного морского пути, развертывании Вооруженных Сил в Арктике, а также в дистанционных системах контроля и управления необслуживаемыми объектами добычи углеводородного сырья в районах Крайнего Севера. Так как наблюдается тенденция к увеличению группировок как отечественных, так и зарубежных спутников, то для предотвращения навязывания спутником-нарушителем ранее прихваченной и задержанной команды управления в работах [1, 2] предлагается применять систему «свой – чужой» для спутников. Снижение времени, необходимого на аутентификацию спутника, позволит повысить информационную скрытность низкоорбитальных ССС. Решить проблему можно за счет использования в системах «свой – чужой» методов аутентификации, реализующих параллельные вычисления с использованием кодов системы остаточных классов (СОК).
Для обеспечения высокой имитостойкости к подбору сигнала ответчика без использования криптографических шифров применяются методы аутентификации на основе протоколов с нулевым разглашением знаний. При этом наибольший интерес представляют протоколы, имеющие один раунд аутентификации. Повысить информационную скрытность ССС возможно за счет повышения скорости процесса аутентификации космического аппарата. Достичь данной цели можно за счет использования модифицированных протоколов, реализованных в модулярных кодах (МК). Данные коды, выполняя параллельно операции сложения, вычитания и умножения, позволяют повысить скорость работы системы «свой – чужой». Целью работы является снижение временных затрат на определение статуса спутника за счет применения кодов системы остаточных классов.
Материалы и методы исследования
Коды системы остаточных классов являются арифметическими непозиционными кодами [3, 4]. Для вычислений целое число X однозначно задается кортежем остатков
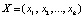, (1)
где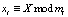 
, mi – основания кода СОК; НОД 
; 
.
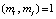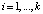Так как основаниями СОК выступали попарно простые числа mi, где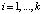 
, то их произведение задает размер рабочего диапазона
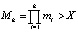. (2)
Так как коды выполняют параллельно операции сложения, вычитания и умножения
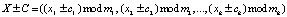, (3)
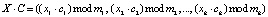, (4)
то их целесообразно использовать для повышения скорости выполняемых вычислений.
Анализ выражений (3) и (4) показал, что коды СОК можно использовать в протоколах аутентификации, в которых используются аддитивные и мультипликативные операции по модулю. Особое место среди последних занимают протоколы, основанные на доказательстве с нулевым разглашением знаний. В работе [5] представлен протокол аутентификации Фиата – Шамира. Рассмотрим модификацию данного протокола в МК.
1. Определяем два больших простых числа m1 и m2 в качестве оснований МК. Тогда согласно (2) их произведение дает диапазон М2, который является частью открытого ключа.
2. Ответчик выбирает случайное число Q, которое является секретным ключом, из условия НОД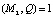 
, 
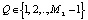. Число переводится в МК Q = (Q1, Q2).
3. Ответчик вычисляет квадратичный вычет L по модулю М2 в модулярном коде. Это вторая часть открытого ключа
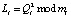. (5)
При этом должно выполняться условие
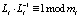. (6)
Процесс аутентификации включает в себя следующие этапы.
4. Ответчик выбирает случайное число R и представляет его в модулярном коде. Затем проводится вычисление числа W и его передача запросчику
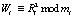. (7)
5. Запросчик, получив W = (W1, W2), выбирает случайное число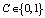 
и передает ответчику.
6. Ответчик вычисляет ответ на поставленный вопрос С:
Уi =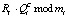 
. (8)
Ответ передается запросчику.
7. Запросчик проверяет истинность ответа при условии:
- если вопрос С = 0, то получаем выражение
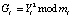, (9)
- если вопрос С = 1, то получаем выражение
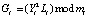. (10)
Проверяемый объект получит статус «свой» если будет справедливым условие
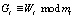. (11)
При невыполнении условия (11) проверяемый объект получает статус «чужой».
В работах [6, 7] представлен протокол аутентификации Гиллоу – Куискуотера, который также относится к протоколам с нулевым разглашением знаний. Проведем его модификацию в модулярном коде СОК.
Для выполнения данного протокола претендент Р должен обладать определенной идентификационной информацией IP. В состав этих данных может входить тип спутника, его личный идентификатор, срок выхода на орбиту, и т.д. На этапе получения открытого и секретного выполняется алгоритм, который состоит из следующих шагов.
1. Выбираются два больших простых числа m1 и m2 , которые являются основаниями МК. Затем находится их произведение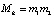 
.
2. Ответчик вычисляет хеш-функцию строки идентификации IP , используя выра- жение
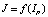, (12)
где f – функция, реализующая процедуры свертки.
3. Ответчик выбирает секретный ключ В = (В1, В2) из условия
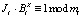, (13)
где i = 1, 2.
Открытым ключом данного протокола являются (M, X, J). Секретным ключом – В.
На этапе проведения аутентификации выполняются следующие этапы.
4. Ответчик выбирает случайное число С, из условия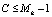 
, и преобразует его в модулярный код. После этого он вычисляет число в МК
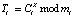, (14)
где i = 1, 2.
Данное число Т = (Т1, Т2) передается на проверяющую сторону запросчику.
5. Запросчик, получив число D, выбирает случайное число из условия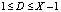 
. Выбранное число пересылается ответчику на борт спутника.
6. Ответчик, получив вопрос D, отвечает на поставленный вопрос
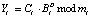. (15)
Вычисленный ответ Y = (Y1, Y2) пересылается запросчику.
7. Запросчик, получив число Y = (Y1, Y2), проверяет правильность ответа
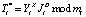. (16)
Если вычисленное значение совпадет с числом Т, то запросчик принимает решение, что спутник имеет статус «свой». В противном случае – спутник получает статус «чужой».
Результаты исследования и их обсуждение
Рассмотрим выполнение протокола аутентификации Фиата – Шамира. Рассмотрим модификацию данного протокола в МК.
1. Пусть выбраны основания кода m1 = 5 и m2 = 7. Тогда согласно (2) их произведение дает диапазон М2 = 35, который является частью открытого ключа.
2. Ответчик вычисляет квадратичные вычеты L по модулю М2 = 35, которые удовлетворяют условию (5). Тогда получаем числа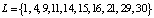 
. Из них условию (6) удовлетворяют 
.
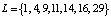Например, если выбрать число L = = 16 = (1, 2), то мультипликативная инверсия по модулю 35 будет равна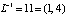 
, так как имеем 
.
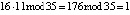3. Ответчик выбирает случайное число Q, которое является секретным ключом, из условия НОД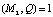 
, 
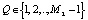. При этом число Q должно удовлетворять выражению (5). Пусть ответчик выбрал число Q = 9 = (4, 2). Возведем его в квадрат
.
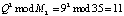В модулярном коде получаем
.
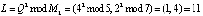Тогда открытым ключом является кортеж (М2, L) = (35, (1, 4)).
Процесс аутентификации включает в себя следующие этапы.
4. Ответчик выбирает случайное число R. Пусть R = 8 = (3, 1). Затем проводится вычисление числа W на основе (6) и его передача запросчику
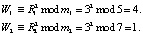
Вычисленное число в модулярном коде W = (4, 1) передается запросчику.
Рассмотрим оба случая проверки статуса объекта, то есть при С = 0 и С = 1.
5.1. Запросчик, получив W = (4, 1), выбирает число С = 0 и передает ответчику.
6.1. Ответчик вычисляет ответ на вопрос С = 0, используя выражение (8):
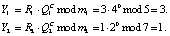
Ответ Y = (Y1, Y2) = (3, 1) передается запросчику.
7.1. Так как запросчик передал С = 0, то для проверки используется (9). Тогда
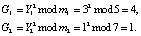
Так как выполняется равенство (11), то объект имеет статус «свой».
5.2. Запросчик, получив W = (4, 1), выбирает число С = 1 и передает ответчику.
6.2. Ответчик вычисляет ответ на вопрос С = 1, используя выражение (8)
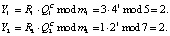
Ответ Y = (Y1, Y2) = (2, 2) передается запросчику.
7.1. Так как запросчик передал С = 1, то для проверки используется (10). Тогда
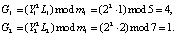
Так как выполняется равенство (11), то объект имеет статус «свой»
Рассмотрим модификацию протокола аутентификации Гиллоу – Куискуотера.
1. Пусть ответчиком выбираются два простых числа m1 = 5 и m2 = 11. Тогда диапазон модулярного кода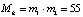 
.
2. Положим, что идентификатор ответчика равен IP = 14367. Затем он вычисляет хеш-функцию согласно (12) в модулярном коде
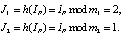
3. Ответчик выбирает секретный ключ В из условия (13), используя МК
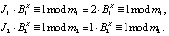
Преобразуем данные равенства и получаем, что
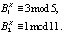
Тогда в качестве секретного ключа В можно взять число В = 3 (3, 3), а показатель степени Х = 5.
Открытым ключом данного протокола являются (M, X, J) = ((5, 11), 5, (1, 2)).
Рассмотрим аутентификацию ответчика. Для этого необходимо выполнить
4. Ответчик выбирает случайное число С = 17 = (2, 6) из условия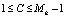 
, а затем вычисляет число
.
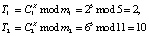Данное число Т = (2, 10) передается запросчику.
5. Запросчик, получив число Т = (2, 10), выбирает случайное число D = 4, из условия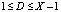 
. Число D = 4 пересылается ответчику.
3. Ответчик, получив вопрос D = 4, отвечает на поставленный вопрос
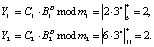
Вычисленный в модулярном коде ответ пересылается запросчику.
4. Запросчик, получив число Y = (2, 2), проверяет правильность ответа
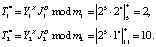
Так как вычисленное значение совпадет с числом Т, то есть Т* = Т = (2, 10), то запросчик принимает решение, что проверяемый спутник «свой».
Рассмотренные модификации протоколов аутентификации, построенные на основе доказательства с нулевым разглашением знаний, можно отнести к многошаговым. При этом для обеспечения высокого уровня криптостойкости протокола аутентификации Фиата – Шамира требуется выполнения от 20 до 40 раундов. Это связано с тем, что вероятность подбора правильного ответа на одном раунде составляет 0,5. Поэтому для снижения такой вероятности необходимо многократное повторение раундов аутентификации.
Для оценки реализации данных модификаций протоколов в модулярных кодах был разработан аппаратный дизайн структурной модели системы опознавания, реализованной на основе 32-разрядного модуля. Построение выполнено на основе ПЛИС FPGA Xilinx Virtex-7 с использованием инструментария Vivado HLS 2019.2. Максимальная тактовая частота устройства составила 250 МГц. Для выполнения мультипликативных и аддитивных операций использовались LUT-таблицы. Сравнительный анализ одного раунда аутентификации, реализованный в модулярных кодах, показал, что для реализации протокола Фиата – Шамира требуется 2,42 ms. При этом временные затраты на один раунд выполнения протокола Гиллоу – Куискуотера составят 3,7 ms. В результате получаем, что реализация одного раунда протокола Фиата – Шамира требует в 1,53 раза меньше временных затрат по сравнению с протоколом Гиллоу – Куискуотера. Однако для достижения требуемой криптографической стойкости к подбору сигнала ответчика для выполнения протокола аутентификации Фиата – Шамира требуется несколько раундов реализации. В этом случае при выполнении 20 раундов опознавания спутника временные затраты составят 48,4 ms. Поэтому модификацию протокола аутентификации Гиллоу – Куискуотера, реализованного в МК, можно считать более эффективной по сравнению с многораундовым проколом Фиата – Шамира.
Заключение
Для повышения эффективности систем аутентификации низкоорбитальных спутников необходимо уменьшать время на процедуру вычисления статуса спутника, так как это позволяет снизить вероятность подбора сигнала ответчика. Для достижения поставленной цели в статье рассмотрены модификации протоколов аутентификации Фиата – Шамира и Гиллоу – Куискуотера, реализованные в МК. Проведенный сравнительный анализ показал, что, несмотря на то, что временные затраты на выполнение одного раунда аутентификации протоколом Фиата – Шамира в 1,53 раза меньше временных затрат по сравнению с протоколом Гиллоу – Куискуотера, на полную аутентификацию спутника потребуется 48,4 ms. На основе полученных результатов исследования можно сделать вывод о том, что модификация протокола аутентификации Гиллоу – Куискуотера, реализованная в МК, можно быть использована для построения систем опознавания спутника.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 20-37-90009.