Установки и технологии, основой функционирования которых является электролиз, называют электрохимическими системами. К ним относят такие промышленные процессы, как электролитическое формование, электролитно-плазменная обработка, электрохимическая защита подземных и подводных металлических сооружений от коррозии, производство цветных и редких металлов, нанесение на детали гальванических покрытий и др. Важную роль в современном машиностроении играет алюминий, производство которого является необходимым условием успешного развития космической, авиационной, автомобильной и других отраслей промышленности. Вопросам проектирования и оптимизации процессов электролиза алюминия посвящены многие экспериментальные и теоретические исследования [1, 2]. Разработка математических моделей процессов, происходящих в электролизерах, отражена, в частности, в работах [3–5]. Сложность моделирования процессов, происходящих в электролизере, обусловлена технологическими ограничениями и взаимным влиянием многих факторов: магнитного и электрического полей, температуры, изменяющегося состава электролита и др. [6–8].
Целью данной работы является построение алгоритма расчета стационарного электрического поля в алюминиевом электролизере в двумерной постановке с учетом различной электропроводности отдельных элементов.
Основные предположения и постановка задачи
Рассмотрим двумерное сечение многоэлементной электролизной системы на примере алюминиевого электролизера с самообжигающимся анодом (рис. 1).
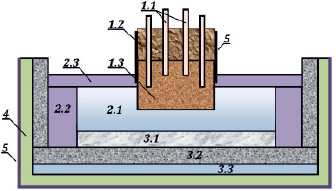
Рис. 1. Сечение алюминиевого электролизера: 1.1 – токоподводящие анодные штыри; 1.2 – анодная масса (расплавленный нефтяной кокс с каменноугольным пеком); 1.3 – спеченный анод; 2.1 – жидкий электролит; 2.2 – гарнисаж (затвердевший электролит); 2.3 – глинозем, корка; 3.1 – жидкий алюминий; 3.2 – угольные блоки; 3.3 – катодный токоподвод; 4 – теплоизоляция. 5 – стальной кожух
Для построения алгоритма все элементы сгруппируем по трем зонам: анодная зона Z1 (элементы 1.1, 1.2, 1.3), зона электролита Z2 (2.1, 2.2, 2.3) и катодная зона Z3 (3.1, 3.2, 3.3). В этом случае область решения представляет собой объединение этих зон: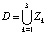 
. Пусть каждая из зон состоит, в свою очередь, из Mk элементов с различными свойствами: 
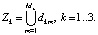Тогда общее число элементов системы равно 
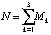, а вся область решения является их объединением: 
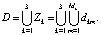Здесь, и далее везде, первый индекс отвечает номеру зоны (1 – анодная зона, 2 – зона электролита, 3 – катодная зона); второй индекс соответствует номеру элемента внутри зоны.
В [9] показано, что потенциал электрического поля φ(p) удовлетворяет уравнению
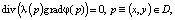(1)
где λ(p) – удельная электропроводимость.
Будем предполагать однородность отдельных элементов, т.е.
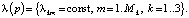
Уравнение (1) необходимо дополнить условиями на границах между отдельными элементами. Заданной величиной является внешнее напряжение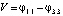 
, приложенное к анодному и катодному токоподводам. Полагая потенциал катодного токоподвода нулевой точкой отсчета (φ3.3 = 0), краевое условие на анодном токоподводе можно записать как
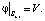(2)
На внешних границах электролизера должны выполняться условия непротекания тока. Такие же условия могут быть поставлены на границах симметрии. Подобные линии (в трехмерной постановке – плоскости) вводятся для сокращения общей длины границ интегрирования. Указанный прием позволяет значительно сократить размерность итоговой системы уравнений, а следовательно, и время расчета, На указанных границах потенциал удовлетворяет условиям [9]:
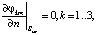(3)
здесь вектор n – нормаль к границе; индекс m принимает значения, которые имеют смысл, т.е. соответствуют изолированным границам.
На границах элементов с различной проводимостью внутри каждой из зон ставятся условия непрерывности плотности тока и потенциала (простые условия сопряжения при идеальном контакте):
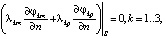(4)
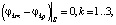(5)
где S – граница между соседними элементами dkm и dkp.
Так как элементы dkm и dkp в данном случае принадлежат одной и той же зоне, то m ≠ p. Индексы m и p принимают значения, соответствующие элементам, имеющим общую границу.
На границах анодных и катодных элементов с электролитом, вследствие наличия двойного электрического слоя, возникает разрыв решения, с учетом которого формируются краевые условия сопряжения (случай неидеального контакта) [10]:
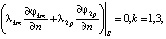(6)
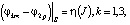(7)
где S – граница между соседними элементами, один из которых принадлежит зоне электролита (k = 2); η(J) – заданная функция поляризации, которая строится по данным экспериментальных измерений. Остальные обозначения в формулах (6), (7) имеют тот же смысл, что и в условиях (4), (5).
В электролизной системе выполняется закон Ома; на границах отдельных элементов он может быть записан в виде краевого условия второго рода:
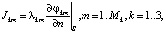(8)
для нормальной составляющей Jkm плотности тока на границах элементов.
Вектор нормали, фигурирующий в краевых условиях, должен иметь определенное направление. Так, если два элемента с номерами m1 и m2 в одной и той же зоне имеют общую границу и при этом m1 < m2, то далее везде условимся считать, что нормаль к границе направлена от m1 к m2.
Балансовые соотношения по току должны выполняться на любом замкнутом контуре:
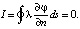(9)
В предложенном алгоритме проверка выполнения (9), т.е. закона сохранения заряда, наиболее просто реализуется по контурам отдельных элементов электролизной системы.
Уравнение (1) с условиями (2)–(7) описывают распределение электрического поля в электролизной системе с однородными свойствами ее отдельных элементов. В сформулированной модели реализована нелинейная зависимость плотности тока от скачка потенциала на границах электролита с элементами анодной и катодной зон. В каждой из зон на границах соприкасающихся элементов установлены простые условия сопряжения.
В системах электролиза, зависимости для поляризации η(J), как правило, во многих случаях описываются логарифмическими функциями [11]. Обратная зависимость J(η), которая используется в предлагаемой модели, может быть описана соотношением [12]:
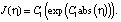(10)
Здесь параметры C1, C2 зависят от свойств граничащих элементов и вычисляются на основе данных эксперимента.
Расчет потенциала в анодной зоне
При построении алгоритма используется тот факт, что в области с однородной средой (в каждом отдельном элементе) потенциал удовлетворяет уравнению Лапласа [9]:
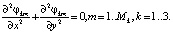(11)
Изложим алгоритм для численного решения задачи, который включает метод граничных интегральных уравнений [12] для каждого элемента, и внешнюю итерационную процедуру. Вначале опишем внутренний итерационный процесс в одной из зон. Пусть это будет анодная зона; в нашем примере она содержит M1 элементов. Для потенциала в этой зоне на основе формулы Грина [10] в каждом элементе строится граничное интегральное уравнение:
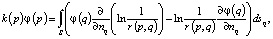(12)
здесь интегрирование проводится по координатам точки q; а решение находится в точке р; k(p) = 2π, если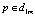 
; k(p) = π, если 
; 
.
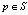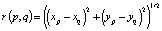Цель дальнейших преобразований в том, чтобы в (12) избавиться от интегрирования по внутренним границам зоны и оставить только внешние границы; тем самым сократить время расчета. Этот прием изложен в [4, 8]; обе части уравнения (12) умножаются на λ1m, затем суммируются по m от 1 до M1 (для краткости опустим аргументы у r(p, q)):
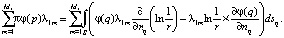
Из последнего соотношения, с учетом условий (4), (5) на границах внутри зоны, проведя тождественные преобразования, несложно получить уравнение для неизвестной функции φ:
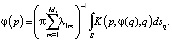(13)
В уравнении (13) ядро определяется из следующих соотношений:
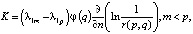
если q лежит на границе между элементами;
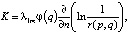
для q, лежащей на границе-изоляторе;
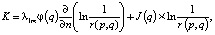
когда q лежит на границе электролита с одним из анодных элементов.
Важно заметить, что в последнем соотношении значение J(q) на границах анод/электролит вычисляется согласно зависимости (10).
В уравнении (13) суммирование производится только по внешним границам анодной зоны, что в итоге значительно сокращает время расчета. Аналогично правилу, изложенному для анодной зоны, выводятся уравнения для катодной зоны и зоны электролита.
Численное решение уравнения (13) последовательно в каждой зоне Zk находится с помощью следующей итерационной процедуры [12]:
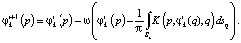(14)
Здесь i – порядковый номер итерации; ω – положительный параметр, значение которого находится из условия сходимости процесса (14) при проведении вычислительных экспериментов. Повторение процедуры (14) происходит до выполнения условия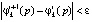 
, для всех 
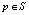и наперед заданного положительного ε. Из внешней итерационной процедуры процесс (14) вызывается поочередно с соответствующими параметрами для каждой зоны Zk.
Внешний итерационный процесс
Общая схема алгоритма состоит из следующих блоков:
a) для граничного потенциала в электролите и электродах (анод и катод) выбирается начальное приближение из физических соображений, после чего рассчитывается по формуле (7) скачок потенциала, а затем, согласно соотношению (10), плотность тока;
b) в зонах анода и катода поочередно выполняется процедура (14), по завершению которой находятся новые приближения для потенциала φ(p) на границах анод/электролит и катод/электролит. Из формулы (7) находятся очередные приближения поляризации η(p), затем вычисляются для плотности тока новые значения J(р) на границах электролита с анодом и катодом;
c) в электролитной зоне осуществляется выполнение процедуры (14), в результате чего потенциал φ(p) получает новые значения на границах; вычисляется поляризация η(p); плотность тока J(р) корректируется новым приближением;
d) закон сохранения заряда (9) проверяется по замкнутым границам анода, электролита и катода. В случае его невыполнения с определенной точностью осуществляется повторение блоков b) и c) изложенного алгоритма.
На рис. 2 представлена блок-схема предложенного алгоритма.
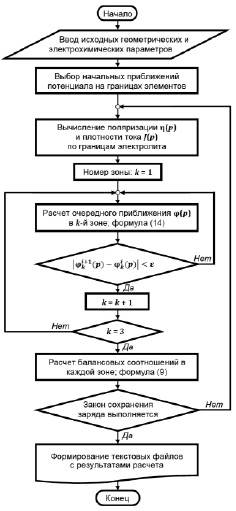
Рис. 2. Блок-схема алгоритма
Заключение
Анализ влияния входных параметров на интенсивность электролиза является одной из целей проведения численных расчетов. Предложенные математическая модель, алгоритм и программный код предоставляют возможность проведения многочисленных расчетов электрических полей в сложных электрохимических системах. В работе в качестве примера приведена упрощенная схема (двумерное сечение) алюминиевого электролизера. Так как основой итерационного процесса является метод граничных элементов, то предложенный подход применим также для решения аналогичных задач в трехмерных областях.