В настоящее время в связи с введением новых стандартов высшего образования все большее внимание ученых и практиков уделяется изучению различных аспектов формирования и развития профессиональных компетенций будущих учителей. Одной из таких компетенций учителей математики является культура математической речи, которой необходимо обучать студентов, готовящихся к этой профессии.
Проведенный нами анализ психолого-педагогической и другой научной литературы позволил выявить сущность понятий «компетентностный подход», «математическая речь», «культура математической речи»; а также рассмотреть их взаимосвязи.
Теоретическую базу нашего исследования составляют работы ученых Б.В. Гнеденко, В.А. Далингер, С.С. Елифантьевой, Д.А. Зуевой, А.С. Монгуш, И.В. Налимовой, И.М. Османовой, О.М. Тановой, М.В. Танзы, Д.В. Шармина, Х.Ш. Шихалиева, посвященные проблеме развития математической речи будущих учителей. Так, например, Х.Ш. Шихалиев, исследовав уровень математической культуры выпускников средней школы, пришел к выводу, что они совершенно не владеют устной и письменной математической речью [1].
В результате изучения трудов вышеназванных ученых сделаны выводы о том, что поднятая проблема является актуальной. Следует подчеркнуть, что развитие культуры математической речи будущего учителя математики процесс довольно-таки сложный и долгий в связи с особенностью, символьностью математического языка.
Компетентностный подход в образовании предполагает освоение обучающимися умений, позволяющих им в будущем действовать эффективно в ситуациях профессиональной, личной и общественной жизни. Это в своих трудах отмечают Ж.Б. Бейсбекова, Ф.А. Меджидова, В.Я. Назмутдинов, Т.А. Разуваева, Г.Р. Юсупова и др. Компетентностный подход является продуктом потребности в специалистах, не только имеющих багаж знаний, но и умеющих эти знания применить на практике. Главными умениями для учителя являются владение математической речью и умелая организация самостоятельной познавательной деятельности обучающихся; использование индивидуальной, групповой и коллективной деятельности в различных сочетаниях.
В настоящее время обуславливается объективная необходимость поиска методических подходов к развитию культуры математической речи в связи с тем, что использование современных информационных технологий, введение дистанционного образования актуализируют необходимость в развитии культуры речи, как одной из основных компетенций будущих учителей математики.
Объект исследования: процесс развития культуры математической речи будущих учителей математики.
Цель исследования: выявить педагогические условия эффективного развития культуры математической речи будущих учителей математики в условиях компетентностного подхода.
Гипотеза исследования: процесс развития культуры математической речи будущих учителей математики будет наиболее эффективным, если будут соблюдены следующие педагогические условия:
- учебный процесс будет организован так, что развитие культуры математической речи будущих учителей математики будет носить системный характер;
- в структуру занятий будут включены интерактивные формы взаимодействия между всеми участниками образовательного процесса;
- будет проводиться систематическая диагностика уровня развития культуры математической речи будущих учителей математики, в ходе которой анализируются, корректируются и вводятся различные формы, методы и технологии обучения.
Для решения поставленной цели нами рассмотрена научно-методическая литература по теме исследования и выявлены основные определения и содержание понятий «компетентностный подход», «культура математической речи», а также приемы работы по развитию математической речи, критерии, уровни сформированности культуры речи.
Так, например, для нашего исследования интерес представляет определение, данное О.Е Лебедевым: «компетентностный подход – это совокупность общих принципов определения целей образования, отбора содержания, организации образовательного процесса и оценки образовательных результатов» [2].
И.В. Налимова и С.С. Елифантьева к специальным приемам работы по развитию математической речи студентов относят:
- «воспроизведение определений, правил, теорем при решении задач;
- стимулирование студентов задавать друг другу вопросы;
- обсуждение хода решения задач;
- решение специальных заданий, направленных на формирование культуры математической речи» [3, с. 75].
В.А. Далингер считает, что формированию культуры математической речи может способствовать специально разработанная система задач, в которую целесообразно включать следующие задания:
- задания, предназначенные для работы с терминологией, символикой и графическими изображениями;
- задания, предназначенные для работы со словесно-логическими конструкциями математического языка;
- задания, предназначенные для работы с письменными обучающими текстами по математике [4].
Д.В. Шарминым показано, что такие критерии, как правильность, точность, логичность, ясность и уместность математической речи, можно рассматривать как некоторый минимальный набор коммуникативных качеств, по совокупности которых можно судить об уровне сформированности математической речи обучающихся в целом [5]. К первому уровню автор относит правильность, точность и логичность; ко второму – ясность и уместность.
Группа ученых из Татарстана, изучив вопрос сформированности коммуникативных качеств математической речи у студентов-билингвов, пришла к выводу, что для определения базовых характеристик «более математически структурированной речи» достаточно рассмотреть правильность, точность и логичность [6].
Теоретический анализ работ и собственное исследование проблемы позволили нам согласиться с коллегами из Татарстана и выделить следующие критерии, которые рассматриваются в работах Д.В. Шармина:
- правильность (П), включающая математическую (МП), орфографическую, пунктуационную и грамматическую (ОПГП), графическую (ГП) составляющие;
- точность (Т) – умение точно выражать свои мысли в устной и письменной речи;
- логичность (Л) – владение основными словесно-логическими структурами математического языка [5].
Эксперимент был проведен на кафедре методики преподавания математики Института математики и информатики Северо-Восточного федерального университета, с охватом 82 студентов разных курсов, в том числе обучающихся заочного отделения, основная часть которых – действующие учителя математики республики.
Основываясь на определении компетентностного подхода О.Е. Лебедева, а также на выявленных И.В. Налимовой специальных приемах работы по развитию математической речи студентов нами разработаны задания по таким дисциплинам, как «Вводный курс математики», «Методика обучения математике», «Современные образовательные технологии в обучении математике», «Элементарная математика» и т.п.
Приведем примеры заданий по дисциплине «Вводный курс математики» для развития и проверки правильности речи по Д.В. Шармину, рассматриваются основные параметры (математическая составляющая, графическая составляющая и грамматические составляющие) [5]:
1. При выполнении данного задания отрабатывается умение переводить символьные записи на математический язык, что является математической составляющей культуры математической речи (МП):
Даны высказывания: M = «Четырехугольник ABCD – параллелограмм», N = = «Диагонали четырехугольника ABCD в точке пересечения делятся пополам». Сформулируйте высказывания, соответствующие формулам: а) M > N, б) N > M, в) 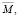 г)
г) 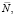 д)
д) 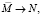 е)
е) 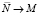 , ж)
, ж) 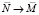 .
.
Решение: а) Если четырехугольник ABCD – параллелограмм, то диагонали четырехугольника ABCD в точке пересечения делятся пополам; б) если диагонали четырехугольника ABCD в точке пересечения делятся пополам, то четырехугольник ABCD – параллелограмм»; в) четырехугольник ABCD – не параллелограмм; г) диагонали четырехугольника ABCD в точке пересечения не делятся пополам; д) если четырехугольник ABCD – не параллелограмм, то диагонали четырехугольника ABCD в точке пересечения не делятся пополам; е) если диагонали четырехугольника ABCD в точке пересечения не делятся пополам, то четырехугольник ABCD – параллелограмм; ж) если диагонали четырехугольника ABCD в точке пересечения не делятся пополам, то четырехугольник ABCD – не параллелограмм. Осмысленность перевода символьной записи на математический язык можно проверить с помощью дополнительного вопроса: истинно или ложно полученное высказывание.
С целью большего охвата обучающихся можно организовать данную работу в диадах, когда студенты проговаривают друг другу полученные высказывания. Затем можно организовать совместную проверку и обсуждение.
2. Выполняя данное задание, студенты учатся переводить из одного вида символьной записи в другой, а также правильно выполнять графические изображения, что относится к графической составляющей культуры математического языка (ГП):
Задание: 1) прочитайте промежутки, 2) задайте числовое множество описанием характеристического свойства элементов, 3) изобразите на координатной прямой перечисленные множества: а) [-4,5; 10); б) [6; +∞).
Решение: а) 1) «полуинтервал от -4,5 до 10, включая -4,5»;
2) характеристическое свойство: A = = {x|x∈R, -4,5 ≤ x < 10};
3) 
б) 1) «числовой луч от 6 до плюс бесконечности»;
2) характеристическое свойство: B = = {x|x∈R, x ≥ 6};
3) 
Данную работу можно организовать как лекцию-визуализацию или, если это изучают на практике, можно использовать технологию Ассессмент-центра, то есть имитировать профессиональную деятельность и предложить студентам провести урок.
3. Орфографическую, пунктуационную и грамматическую составляющие правильности речи (ОПГП) можно развивать и проверять с помощью диктантов. Приведем примеры некоторых заданий таких диктантов:
а) терминологический диктант (запись под диктовку основных терминов): кортежи, отображения, бинарное отношение, рефлексивность, симметричность, транзитивность, эквивалентность, прообраз, сюрьективность, инъективность, биективность, композиция.
б) данная форма работы используется во время лекции. Обучающимся предлагается записать под диктовку определение: конъюнкцией (логическим умножением) двух высказываний x, y называется новое высказывание, которое считается истинным, если оба высказывания x и y истинны, и ложным, если хотя бы одно из них ложно (т.е. в остальных случаях). Далее проверяется пунктуация и предлагается самостоятельно составить по записанному определению таблицу истинности конъюнкции.
Затем, работа над понятием дизъюнкция проводится наоборот: дается таблица истинности, студенты должны написать определение по аналогии с определением конъюнкции.
Таким образом, формируется коммутативное качество «ясность», показатель второго уровня сформированности культуры математической речи обучающихся;
в) грамматическую составляющую правильности речи можно развивать с помощью следующих заданий, которые можно использовать во время лекции-диалога: нарисовать на доске два графа и задать следующие вопросы:

А. Который из графов будем называть ориентированным графом или орграфом? Неориентированным графом? Обоснуйте свой ответ.
Б. Какую из вершин можно назвать изолированной вершиной? Висячей вершиной? Обоснуйте свой ответ.
В. Назовите подграф неориентированного графа. Обоснуйте свой ответ.
Так как грамматика – это раздел лингвистики, который изучает строение слов (словообразование), то на ее основе обучающиеся учатся понимать термин и, в данном случае, определять его на рисунке. Также с помощью данного задания можно проверить сформированность второго уровня культуры математической речи – коммутативное качество речи «ясность», которое определяется Д.В. Шарминым как «осознание предмета речевого сообщения, которое характеризуется обоснованностью проводимых рассуждений, умением самостоятельно приводить иллюстрирующие материал примеры и объяснить их» [5].
Развитие культуры математической речи будущих учителей математики будет носить системный характер, если этим будут заниматься все преподаватели. Поэтому приведем ещё примеры организации работы студентов на занятиях по дисциплине «Методика преподавания математики».
При изучении специальной методики важное место отводится самостоятельной работе с учебно-методической литературой в ходе самоподготовки обучающихся к аудиторным занятиям. Самостоятельные работы включают в себя такие задания, как:
- ознакомьтесь с материалами п. 19 учебника Ю.Н. Макарычева и др. «Алгебра 9» и решите с комментарием учителя № 435 (а); спланируйте индивидуальную учебную деятельность обучающихся, в том числе с особыми образовательными потребностями;
- объясните, какие сдвиги параболы y = x2 приводят к построению графика функции: а) 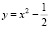 ; б) y = (x + 7)2; в) y = (x + 4)2 – 5;
; б) y = (x + 7)2; в) y = (x + 4)2 – 5;
- восстановите следующее утверждение: Если при … двух прямых … соответственные … равны, то прямые …;
- разработайте мотивационный материал для изучения темы «Отрицательные числа» с применение аудиовизуальных средств обучения;
- Найдите ошибки в речи ученика, комментирующего выполнение задания № 589:
Преобразуйте в многочлен стандартного вида:
а) 18x2 – (10x – 5 + 18x2) = раскрываем скобки, перед которыми стоит знак минус, скобки опускаем, а знаки меняем на противоположные = 18x2 – 10x + 5 – 18x2 = сокращаем 18x2, получим = –10x + 5.
На занятиях по дисциплине «Методика обучения математике» активно используются различные методы и технологии обучения, такие как метод проектов, кейс-технологии, дебаты, деловая игра, мастерская, «Атака мыслей», «Ищи ошибку», «Перевернутый класс», проблемное обучение, модульное обучение, информационно-коммуникационные технологии и др.
Показатели основных параметров, характеризующих культуру математической речи обучающихся (среднее арифметическое по группе)
|
Коммутативные качества речи |
ЗМПО-16 (10 чел.) |
МПО-16 (25 чел.) |
МПО-18 (23 чел.) |
МПО-19 (24 чел.) |
|||||
|
На начало |
На конец |
На начало |
На конец |
На начало |
На конец |
На начало |
На конец |
||
|
П |
МП |
3,20 |
3,50 |
2,32 |
3,20 |
2,40 |
2,96 |
2,33 |
2,54 |
|
ОПГП |
3,20 |
3,60 |
2,44 |
3,28 |
2,13 |
2,80 |
2,33 |
2,38 |
|
|
ГП |
3,0 |
3,30 |
2,12 |
3,02 |
1,96 |
2,72 |
2,17 |
2,29 |
|
|
П (ср.ар.) |
3,13 |
3,47 |
2,29 |
3,33 |
2,16 |
2,83 |
2,77 |
2,40 |
|
|
Т |
3,0 |
3,20 |
2,08 |
2,52 |
2,08 |
2,36 |
1,92 |
2,08 |
|
|
Л |
2,80 |
3,20 |
1,96 |
2,44 |
1,88 |
2,18 |
1,75 |
1,96 |
|
Таким образом, на занятиях создаются условия для развития культуры математической речи на основе системной работы, использования различных методов и технологий обучения. При этом нами постоянно проводился мониторинг сформированности культуры математической речи обучающихся, и дальнейшая работа велась с учетом полученных результатов.
Итоги опытно-экспериментальной работы за период с 2014 по 2020 г. свидетельствуют о том, что у студентов значительно повысилась культура математической речи. Отметим, что результаты десяти обучающихся заочного отделения оказались несоизмеримы с результатами бакалавриата, так как за их плечами уже не один год работы в качестве учителя математики.
В данной статье приведем результаты среднеарифметических значений по группам, подсчитанные по методике, предложенной Д.В. Шарминым [5] (таблица).
Как видим из таблицы, значительное развитие культуры математической речи показали студенты всех групп; заметим, что студенты группы МПО-16 – это уже выпускники, дипломированные бакалавры, а МПО-18 и МПО-19 еще продолжают учиться на третьем и втором курсах соответственно. Работа с данными обучающимися будет еще продолжена.
Полученные результаты говорят о том, что разработанные задания и созданные педагогические условия: системность развития культуры математической речи обучающихся, использование интерактивных методов обучения, постоянный контроль, анализ, корректировка различных форм, методов и технологий обучения – способствовали достижению поставленной цели.



