Формирование профессиональной компетентности инженера включает в себя изучение графических дисциплин, которые позволяют овладеть методом проецирования. Проецирование – основа построения изображений конструкторского графического документа – чертежа. Чертеж детали, сборочной единицы – это необходимый этап технологической цепочки изготовления любого технического объекта, к которому и подготавливает изучение графических дисциплин.
Наиболее трудно воспринимаемой студентами графической дисциплиной становится начертательная геометрия, обучающая теоретическим основам построения чертежей простых геометрических объектов: точки, прямой, плоскости, поверхности. При кажущейся простоте этих объектов выявляется сложность построения их проекций, обусловленная тем, что эти объекты с точными математическими характеристиками абсолютно не наглядны, не материальны и их взаимоотношения (параллельность, перпендикулярность, пересечение) при параллельном проецировании совсем не очевидны. Например, на рис. 1 (часть 1) прямые AB и BC не составляют прямой угол – как это показано на горизонтальной и фронтальной проекциях этих прямых. Часть 2 рис. 1 содержит чертеж перпендикулярных прямых AB и BC.
Неочевидность взаимного расположения простых геометрических объектов в проекциях или сложная пространственная конструкция линий пересечения объемных поверхностей, изображаемые проекциями кривой линии, а также другие сложные графические построения, свойственные начертательной геометрии, вызывают трудности у студентов. Это приводит к тому, что обучаемые решают графические задачи при изучении начертательной геометрии, не используя пространственное воображение, чтобы представить графические объекты и понять суть проблемы (например, что представляет пересечение поверхностей), а просто применяя изученный алгоритм. Решение задачи по алгоритму представляет собой воспроизведение корректной и точной последовательности построений, которые дают возможность найти графическое решение задачи. При этом трехмерное представление обучаемых не формируется должным образом, не развивается пространственное мышление, необходимое представителю инженерной специальности [1].
Цель исследования – разработать методику применения трехмерного моделирования в системе Компас 3D на примере выполнения практической работы по теме «Пересечения поверхностей способом вспомогательных сфер вращения».
Материалы и методы исследования
При проведении исследования использовались следующие методы: анализ психолого-педагогической и методической литературы по изучаемой проблеме, педагогическое наблюдение, накопление и отбор фактов, анкетирование, беседа, анализ результатов самостоятельной работы студентов, эксперимент, метод экспертных оценок.
Был проведен анализ существующей литературы по теме использования трехмерного моделирования при решении задач по начертательной геометрии, при введении элементов трехмерного моделирования в учебный процесс осуществлялось наблюдение за успеваемостью студентов, проводилось анкетирование, беседы со студентами, анализ самостоятельных работ на предмет использования трехмерного моделирования в ходе их выполнения, таким образом, реализовался научный эксперимент с экспертной оценкой результатов.
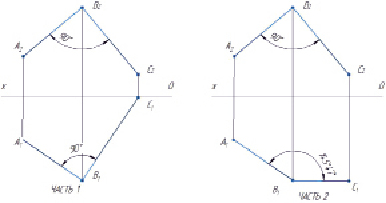
Рис. 1. Перпендикулярные прямые
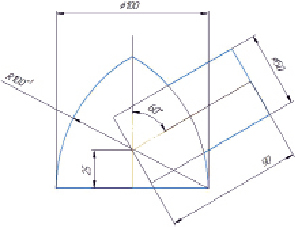
Рис. 2. Условие задачи
Результаты исследования и их обсуждение
Рассмотреть на примере решения задачи по определению линии пересечения поверхностей методом вспомогательных секущих сфер вращения методику применения виртуального моделирования в процессе решения задачи. Решение задачи по алгоритму состоит в следующем.
Главные условия применения способа сечений вспомогательными секущими сферами:
- заданные тела должны быть телами вращения;
- оси тел вращения должны пересекаться;
- оси тел вращения должны быть параллельны одной из плоскостей проекций.
Основные положения данного способа [2]:
1. Центр вспомогательных секущих сфер – точка пересечения осей тел вращения.
2. Радиус сферы максимум равен расстоянию от центра вспомогательных сфер до наиболее удаленной точки линии пересечения.
3. Сфера минимум должна пересекать одну поверхность и касаться другой поверхности.
Вспомогательные сферы должны пересекаться с поверхностями по таким окружностям, которые на плоскости проекций проецируются отрезками прямых или окружностями.
Рассмотрим решение задачи на пересечение закрытого тора и цилиндра. Способ решения задачи – при помощи вспомогательных сфер вращения, центр которых находится в точке пересечения осей вращения поверхностей. Условия задачи приведены на рис. 2.
Необходимо построить линию пересечения заданных поверхностей.
1. Строим сферу максимум и сферу минимум (рис. 3).
2. Для нахождения точек 2, 4, 5 используем вспомогательные секущие сферы, радиус которых больше сферы минимум, но меньше сферы максимум.
3. Определяем видимость линии пересечения и геометрических тел, считая тор целым телом, а цилиндр – усеченным (рис. 3).
В результате решения задачи был построен чертеж линии пересечения поверхностей вращения с применением способа вспомогательных сфер. Обучаемый освоил алгоритм построения в проекции, научился определять линии пересечения соосных поверхностей (отрезки) и находить их общие точки. При решении задач способом сфер очень важно понимать, что линии – отрезки, которые позволяют получать общие точки поверхностей вращения – это проекции окружностей, плоскости которых перпендикулярны данной плоскости проекций. Но чертеж не позволяет наглядно увидеть конструкцию линии пересечения и элементы построения общих точек поверхностей. Для усиления наглядности можно использовать виртуальное моделирование при помощи систем автоматизированного проектирования, например программы КОМПАС 3D V17. Эта программа дает возможность построить модель пересекающихся поверхностей и те вспомогательные сферы вращения, при помощи которых происходит построение линии пересечения [3].
Рассмотрим технологию построения виртуальной модели тела вращения на рис. 4.
Для того чтобы создать виртуальные модели поверхностей вращения, которые заданы в условии задачи, необходимо использовать операцию «Элемент вращения». Для построения элемента вращения нужно выбрать плоскость для построения эскиза, который обязательно должен содержать сечение элемента вращения и, возможно, ось вращения.
Для построения поверхности тор выбираем плоскость ZX и строим ось вращения штрих-пунктирной линией и дугу радиусом 100 мм, образующую сечение операции вращения.
Для построения цилиндра создаем эскиз в плоскости ZY. Эскиз должен содержать ось вращения цилиндра, построенную штрихпунктирной линией и параллельную ей линию сечения, выполненную основной линией.
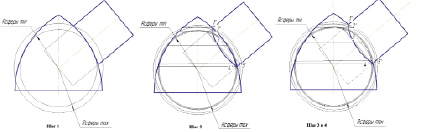
Рис. 3. Решение задачи. Строим проекции сечений поверхностей сферой минимум – получаем точку 3 и сферой максимум – получаем точку 1, которые будут принадлежать одновременно обеим поверхностям, а значит, и линии их пересечения
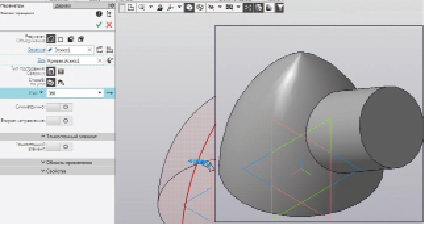
Рис. 4. Построение моделей тел вращения
Выполнив вышеописанные действия, обучаемый может увидеть то, что ему необходимо построить при помощи способа сфер на эпюре (чертеже), виртуально воплотить конечный результат задачи. Но при этом он не сможет понять принцип построения при помощи вспомогательных сфер, не научится соотносить свои пространственные представления, полученные при виртуальном моделировании, с теми построениями, которые были сделаны при решении задачи. Введение в методику решения задачи построения виртуальной модели пересекающихся поверхностей – это использование возможностей компьютерных технологий для усиления наглядности абстрактно-теоретической дисциплины. Построение модели пересекающих поверхностей – это виртуальная презентация пространственных линий пересечения поверхностей, доступная любому обучающемуся [4].
Затем соотнесем виртуальную презентацию элементов решения задачи, в частности вспомогательных сфер посредников. Чтобы не повторяться, рассмотрим один шаг в решении задачи с его виртуальной презентацией. Обратимся к рис. 2, шаг 2, и выполним построение сферы для нахождения точки 2 в виртуальной модели. Для этого поменяем свойства элементов построения: изменим цвет поверхностей. Создадим эскиз в плоскости ZY. Спроецируем поверхности цилиндра и тора в эскиз при помощи команды «Спроецировать объект», обозначим вспомогательными линиями оси вращения, построим дугу, образующую тор, и линию, образующую цилиндр. Построим окружность радиусом большим, чем Rсферы min, и меньшим, чем Rсферы max. Это и будет сфера, необходимая для нахождения любой промежуточной точки, такой как 2, 3, 4. Оставим только половину окружности, удалим лишние элементы и применим команду «Элемент вращения». Получаем виртуальную модель сферы, тора и цилиндра, которая демонстрирует:
- линию пересечения тора и сферы;
- линию пересечения цилиндра и сферы;
- получение общей точки цилиндра и тора;
- линию пересечения тора и цилиндра.
Опишем подробнее этот шаг в построении на чертеже при помощи ассоциативного чертежа с комбинированной модели. На рис. 5 приведены три изображения:
- виртуальная комбинированная модель тор, цилиндр, сфера, позволяющие построить точку 2, тора и цилиндра (рис. 5, часть 1);
- ассоциативный вид виртуальной модели, выполненный в программе Компас 3D V17 (рис. 5, часть 2);
- дополненное на основе вида модели построение точки 2.
Рассмотрим подробнее построение точки 2 (рис. 5, часть 3). В ассоциативный чертеж комбинированной виртуальной модели внесем элементы оформления чертежа: осевые линии, изображения максимальной и минимальной сферы, с обозначенными радиусами, очерковые линии сферы, тора и цилиндра. При этом мы используем еще одну возможность программы «Компас» [5]: работу с командами панелей «Геометрия», «Размеры», «Обозначения».
После этого, используя имеющуюся на чертеже сферу, определяем линии пересечения соосных поверхностей, используя команду «Отрезок», и находим их общую точку 2, которую обозначаем при помощи команды «Надпись».
Соотношение этапов ранее предложенной нами методики [4] и методики, описанной в данной статье, приведено в таблице.
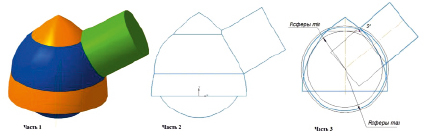
Рис. 5. Поэтапное построение точки линии пересечения тора и цилиндра при помощи виртуальной модели
Соотношение этапов решения задачи
|
Этапы решения задачи, приведенные в ранее описанной нами методике |
Уточненные этапы решения задачи |
|
Построение виртуальной модели пересекающихся поверхностей |
Построение виртуальной модели (Модель 1 рис. 4) пересекающихся поверхностей |
|
Просмотр при помощи Команд «Панели быстрого доступа» |
Просмотр при помощи Команд «Панели быстрого доступа» |
|
Построение ассоциативного чертежа пересекающихся поверхностей |
Введение в виртуальную модель вспомогательного элемента (рис. 5, часть 1) а: сферы – поверхности посредника, позволяющего наглядно показать построение общей точки |
|
Оформление чертежа и выполнение построения точек линии пересечения при помощи команд панели «Геометрия» |
Просмотр при помощи Команд «Панели быстрого доступа» |
|
Результат: задача решена |
Построение ассоциативного чертежа комбинированной модели со сферой (Модель 2, рис. 5) и оформление этапа построения одной из точек линии пересечения |
|
Построение ассоциативного чертежа пересекающихся поверхностей (по модели 1) |
|
|
Оформление чертежа и выполнение построения точек линии пересечения при помощи команд панели «Геометрия» |
|
|
Результат: задача решена |
Введение в решение задачи дополнительных этапов виртуального моделирования обусловлено тем, что важен не только конечный результат и наглядное представление его для обучаемого, важно и понимание способа решения задачи, создание пространственного представления о вспомогательных поверхностях, поверхностях посредников. Это основополагающая информация, теоретический фундамент, правило построения линии пересечения соосных поверхностей. Форма этих линий – окружность, плоскость которой перпендикулярна плоскости проекции, которой параллельны оси вращения пересекающихся поверхностей. И эта важная для обучаемых информация должна быть представлена им наглядно, в виде пространственной презентации. Такая презентация возможна с помощью моделирования в программе Компас [6].
Рассмотрим преимущества предлагаемой нами методики решения задачи.
На современном этапе развития производства особенно актуально введение в учебный процесс изучения компьютерных технологий. Чем раньше вводим в систему графической подготовки изучение компьютерной графики, тем нагляднее, иллюстративнее происходит процесс проецирования преобразования трехмерного представления о детали в двухмерную проекцию чертежа. Это не отменяет того факта, что чертеж остается основным документом, содержащим всю информацию об изделии. Построению, оформлению и содержанию различных видов чертежей необходимо обучать будущих инженеров.
Введение компьютерных технологий происходит в двух важных аспектах: обучение построению элементов двухмерного изображения, обучение разработке виртуальных моделей. Второе невозможно без первого, поскольку обязательным этапом создания модели является эскиз – двухмерное изображение, задающее основные характеристики создаваемого в модели элемента. Наша методика позволяет освоить элементы моделирования и изучить инструменты построения двухмерных изображений на начальных этапах графической подготовки, при изучении начертательной геометрии, закладывающей теоретические основы построения проекций. При этом в процессе обучения теоретическим основам построения чертежа получают дополнительную мотивацию обучаемые, имеющие слабое пространственное воображение и поэтому трудно воспринимающие абстрактный учебный материал. В результате знания теории применены при решении практического задания, проведена апробация правильности решения задачи путем построения виртуальной модели пересекающихся поверхностей. Способ решения задачи продемонстрирован наглядно и стал визуально доступным для понимания.
Заключение
Рассмотрев преимущества данной методики решения задач по начертательной геометрии, можно сделать вывод о том, что современные технологии необходимо внедрять в учебный процесс на начальных этапах графической подготовки. Это позволяет сформировать у обучаемых знания, умения и навыки работы с компьютерными системами разработки чертежа и добавить наглядность и презентативность в процесс изучения теоретических основ построения проекций.



