В финансово-хозяйственной деятельности любого предприятия микроэлектронной промышленности можно выделить большое количество задач, требующих автоматизации. В настоящее время для управления предприятиями используются системы АСУ и ERP.
При этом следует учесть, что управление предприятиями при использовании АСУ происходит по отдельным технико-экономическим критериям подсистем предприятий (основной – производственной и вспомогательных – материально-технического снабжения, технико-экономической, финансовой, складского хозяйства, логистики, управления кадрами и др.) автономно. При использовании же ERP систем управление происходит по совокупности технико-экономических критериев подсистем предприятий – комплексно [1].
Установление понятия кроссированных объектов – объектов ERP-управления. Свойство выходной мажоритарной мультиплицированности этих объектов
Такой переход от отдельных критериев управления к системе критериев управления сопровождается операцией кроссировки подсистем предприятий, т.е. образования между этими подсистемами кроссирующих (от англ. cross – скрещивающий, перекрестный) продольных и поперечных связей, и, соответственно, сопровождается образованием кроссированных объектов ERP-управления (рис. 1).
Речь идёт об образовании связей: основной – кроссируемой подсистемы с подсистемами вспомогательными – кроссирующими. При этом такая операция кроссировки сопровождается сохранением связей «продольных» и образованием новых связей – «поперечных».
Такое образование связей «поперечных» при сохранении связей «продольных» приводит к превалированию числа выходных переменных кроссированного объекта над числом его входных переменных. Назовем такое превалирование числа выходных переменных любого объекта управления (в том числе и объекта ERP) над числом его входных переменных свойством выходной мажоритарной мультиплицированности объектов ERP-управления.
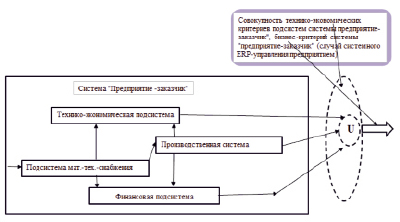
Рис. 1. Функциональная схема кроссированных объектов управления
На рис. 2 представлена блочная схема кроссированных объектов ERP-управления предприятиями в системе обозначений из теории многосвязного управления Меерова – Месаровича [2, 3].
В данном случае это схема с условным обозначением имеющего место у кроссированных объектов ERP управления предприятиями свойства мажорирования (>) n выходными переменными X числа m переменных входных U.
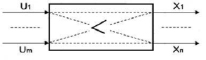
Рис. 2. Иллюстрирование свойства мажорирования (>) обозначением свойства мажорирования (>) n выходными переменными X числа m переменных входных U
Обратим внимание на то, что порождаемое описанной кроссировкой подсистем предприятий – объектов ERP-управления свойство выходной мажоритарной мультплицированности объектов ERP-управления, в свою очередь, приводит к координатной неуправляемости по Р. Калману [4] этих объектов. В данном случае речь идет о неуправляемости именно координатной, а не параметрической. А это значит, что при обращении к управляющим параметрам таких координатно неуправляемых объектов они становятся уже управляемыми.
Обоснование феномена координатной неуправляемости кроссированных объектов управления по Р. Калману
На рис. 3 представлена блок-схема простейшего – элементарного, кроссированного объекта управления, для которого проводится доказательство означенного феномена Р. Калмана.
Обоснование феномена координатной неуправляемости по Р. Калману будет осуществляться на математической модели – системе уравнений, именно элементарного кроссированного объекта управления, и будет осуществляться по критерию, обратному известному «по наихудшему случаю».
Таким образом, будет осуществляться по критерию «наилучшего случая». Здесь – «наилучшего случая» именно элементарного кроссированного объекта. Потому что доказанная для элементарного кроссированного блока неуправляемость, в случае кроссированного объекта более сложного – неэлементарного, будет иметь место тем более.
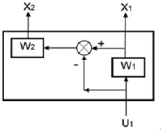
Рис. 3. Блок-схема простейшего кроссированного объекта управления, где W1 – передаточная функция кроссируемой основной (производственной) подсистемы и W2 – передаточная функция какой-либо из вспомогательных подсистем
Математическую модель элементарного кроссированного объекта можно представить в виде такой системы уравнений нормальной формы Коши, взятой в пространстве состояний [5, 6]:
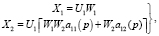(1)
где U1 – входная переменная кроссированного объекта управления;
X1, X2 – выходные переменные кроссированного объекта управления.
Рассмотрим случай управления кроссированным объектом, при котором учитывается только выходная переменная.
Этому случаю управления отвечают единичные значения постоянных коэффициентов в системе уравнений (1), такие как a11 = 1 и a12 = –1.
В этом случае система уравнений (1) принимает вид
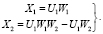(2)
Применительно к системе уравнений (2), будем рассматривать простейший случай инерционных звеньев первого порядка W1, W2 так что
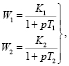(3)
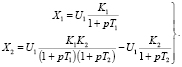(4)
Представленная выше форма уравнений (3) – наличие знаменателей у входной переменной объекта управления не позволяет привести их к нормальной матричной форме Коши («форме Р. Калмана») [6].
Выход: введение вспомогательных переменных:
y1, y2, где py1 = b1y1 + b2U1, py1 = y2 и z1, z2,
где
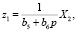
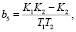
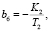
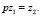
В случае подстановки введённых переменных в уравнения (1) оно принимает требуемую форму Р. Калмана:
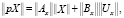(5)
где
, 
.
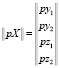
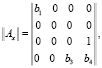
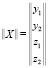Далее отметим, что в общем случае кроссированного объекта для его уравнения в форме Р. Калмана так называемая матрица Р. Калмана имеет вид
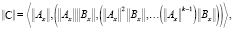(6)
где k – размерность, т.е. составляющая размера dim (k x k) квадратной матрицы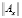 
.
Доказательство феномена координатной неуправляемости по Р. Калману кросcированных объектов ERP-управления
В рассматриваемом случае кроссированного блока (рис. 3), в соответствии с (5), k = 4, тогда матрица управляемости Р. Калмана (6) будет выглядеть как
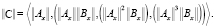(7)
Как показано в [7, 8], для линейного стационарного матричного уравнения, каким является уравнение (5), критерий Р. Калмана – необходимое и достаточное условие координатной управляемости системы, заключается в необходимой и достаточной невырожденности матрицы управляемости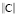 
(6) Р. Калмана.
А это значит, что условием такой управляемости системы является необходимое и достаточное равенство ранга rank – числа n, матрицы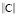 
(6) размерности k квадратной матрицы 
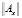размера dim (k x k). То есть условием управляемости исследуемой системы является критерий
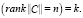(8)
Или для кроссированного объекта управления (рис. 3) таким необходимым и достаточным условием координатной управляемости является следующее равенство:
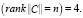(9)
В то же время, как также показано в [8], необходимое и достаточное условие координатной неуправляемости системы заключается в вырожденности матрицы управляемости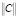 
(20) Р. Калмана.
Тогда условием координатной неуправляемости системы является условие
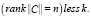(10)
Для кроссированного объекта правления (рис. 3):
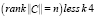. (11)
Это означает, что действительно имеет место феномен: всякий кроссированный объект управления предприятием (объект управления систем ERP), обладающий свойством выходной мультиплицированности, оказывается координатно неуправляемым по Р. Калману.
Следует отметить, что неполная управляемость систем заключается в факте одного только изменения выходных управляемых переменных систем под воздействием входных управляющих переменных.
В то же время полная управляемость заключается не только в изменении выходных управляемых переменных систем под воздействием входных управляющих переменных, но и в достижении при этом заданных значений выходных управляемых переменных [7].
А это значит, что в названном отношении понятия неполной управляемости и неуправляемости, когда в результате воздействия входных управляющих переменных не могут быть достигнуты заданные значения выходных управляемых переменных, являются тождественными.
В случае кроссированного объекта управления (рис. 3) причиной проявления неуправляемости при большем, например равном k = 3, ранге матрицы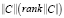 
является наличие двух нулевых строк в матрице 
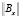входа кроссированного объекта управления (рис. 3) (случай одной входной управляющей переменной U1 при двух выходных управляемых переменных X1, X2).
При этом стоит отметить, что для неуправляемости системы, по Р. Калману, достаточно наличия в матрице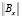 
уже и одной нулевой строки [8].
При этом следует отметить, что и в общем случае всех кроссированных объектов, у которых алогично число n выходных управляемых переменных Xj, j = 1÷n превышает число m переменных Ui, i = 1÷m входных управляющих эффект наличия многих (больше двух) нулевых строк в матрице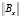 
входа кроссированных объектов только усиливается.
Эффект кроссированности усиливается тем более, чем в большей степени имеет место превалирование числа n выходных управляемых переменных Xj, j = 1÷n над числом m входных управляющих переменных Ui, i = 1÷m.
В отмеченном выше общем случае кроссированных объектов эффект наличия многих нулевых строк в матрице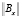 
входа кроссированных объектов будет тем большим, чем большее число n выходных управляемых переменных Xj, j = 1÷n превалирует над числом m входных – управляющих переменных Ui, i = 1÷m.
Получается, что по мере увеличения степени кроссированности блоков систем ERP эффект превалирования показателей k матриц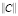 
над рангами матриц 
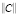, рангов матричных кортежей будет только возрастать.
Вместе с возрастанием этого эффекта будет возрастать, по причине увеличения степени кроссированности, и степень неуправляемости кроссированных объектов управления систем ERP.
Тогда феномен координатной неуправляемости по Р. Калману объектов ERP-управления можно сформулировать следующим образом.
Всякая кроссированность объектов управления систем ERP приводит к их координатной неуправляемости.
И эта неуправляемость является тем более сильной, чем большая степень кроссированности этих систем имеет место.
Заключение
В статье приведены теоретические попытки обосновать феномен неуправляемости, возникающей из-за наличия эффекта мультиплицированности, при переходе от управления системой «предприятие – заказчик» по отдельным технико-экономическим критериям подсистем предприятий (случай АСУ) к управлению по совокупности технико-экономических критериев подсистем предприятий (случай ERP систем).
При этом такой переход сопровождается возникновением эффекта кроссировки подсистем системы «предприятие – заказчик», т.е. образования между этими подсистемами кроссирующих продольных и поперечных связей. При этом такая операция кроссировки сопровождается сохранением связей «продольных» и образованием новых связей – «поперечных». Такое образование связей «поперечных» при сохранении связей «продольных» приводит к превалированию числа выходных переменных кроссированного объекта над числом его входных переменных. Такое превалирование числа выходных переменных любого объекта управления над числом его входных переменных называется свойством выходной мажоритарной мультиплицированности объектов управления. Обратим внимание на то, что порождаемое описанной кроссировкой подсистем предприятий – объектов ERP-управления свойство выходной мажоритарной мультиплицированности объектов ERP-управления, в свою очередь, приводит к координатной неуправляемости по Р. Калману этих объектов. Обоснование феномена координатной неуправляемости по Р. Калману такими объектами авторами показано на математической модели.