Пенобетоном называют разновидность ячеистого бетона, представляющего собой искусственный каменный материал пористой структуры, изготовленный из вяжущего, кремнеземистого компонента, порообразователя и воды [1]. Отличительной особенностью пенобетона, по сравнению с другими разновидностями легких и особо легких бетонов, является трудность достижения стабильных значений показателей качества. Зачастую это связано с необходимостью управления многочисленным количеством рецептурных и технологических факторов [2]. Наиболее распространенным методом решения данной задачи является применение аппарата математического моделирования с элементами статистического анализа.

Для объективного отображения технологического процесса приготовления пенобетона необходимо, чтобы его математическая модель включала все факторы, существенно влияющие на выходную величину [3]. Отсутствие в модели хотя бы одного из существенных факторов может повлечь за собой ошибочную интерпретацию явлений, происходящих в технологическом процессе.

Процесс приготовления и твердения пенобетона сопровождается параллельным протеканием ряда химических и физических процессов. Косвенными показателями этих процессов можно рассмотреть перечень рецептурных факторов. По оценкам многих исследователей, количество факторов, влияющих на свойства пенобетона, может быть достаточно обширным – от пяти до нескольких десятков [1, 4]. Степень влияния этих факторов на выходные данные весьма неоднозначна и зависит от типа исследуемых параметров: средняя плотность, прочность при сжатии, коэффициент теплопроводности, трещиностойкость, морозостойкость и т.д.

В анализе факторов и их оптимизации во многих отраслях промышленности используют так называемый принцип Парето. Принцип является своего рода условным эмпирическим правилом, названным в честь итальянского инженера и экономиста Вильфредо Парето. Сам принцип формулируется следующим образом: «20 % усилий дают 80 % результата, а остальные 80 % усилий – 20 % результата» [5]. В данном контексте это можно перефразировать так: «20 % факторов влияют на 80 % показателей, а остальные 80 % факторов – на 20 % показателей». Приведенная пропорция с математической точки зрения не является точной закономерностью, а служит некоторым обобщающим мнемоническим правилом. Ранжирование факторов по степени влияния на изменчивость показателей качества пенобетона можно достигнуть с использованием принципа Парето. В работе приводится анализ технологического процесса изготовления пенобетонных блоков автоклавного твердения плотностью D500-600 («D» показывает марку пенобетона по средней плотности, кг/м3). Задачей является получение математической модели без отрыва от действующего производства с использованием отработанной рецептуры.

В исследовательских работах по строительному материаловедению обычно применяют аппарат математического планирования эксперимента, либо другие смежные методы, основанные на принципах математической статистики: априорное ранжирование факторов, дисперсионный анализ, регрессионный анализ, комбинаторный анализ (греческие и латинские квадраты и др.), методы экспериментального отсеивания факторов с насыщенными матрицами, метод случайного баланса и т.п. [6]. Каждый из перечисленных методов обладает своими преимуществами и недостатками, а также рядом специфических условий, при соблюдении которых можно получить модель, адекватно отражающую значимость каждого фактора. Следует отметить, что большинство рассмотренных методов в той или иной степени пересекаются с принципами планирования эксперимента. Одним из известных недостатков планирования эксперимента является управление крайне ограниченным количеством входных факторов вследствие необходимости проведения большого количества опытов. Количество опытов N при полном факторном эксперименте рассчитывается по формуле

N = nt, (1)

где n – уровни варьирования факторов, ед.; t – количество факторов в эксперименте.

Например, при n = 3 и t = 2 количество опытов равно 9, при t = 3 количество опытов достигнет 27, а при t = 5 будет равно 243. Таким образом, при планировании эксперимента крайне трудно составить модели, учитывающие более 2–3 факторов. На основании изложенного перед исследователем стоит важная задача – выделить наиболее значимые факторы, так как в противном случае возрастает объем экспериментальной работы и, как следствие, трудоемкость исследовательского процесса. Наиболее целесообразным методом в приведенных ограничениях является регрессионный анализ, в частности элементы множественной регрессии. Назначение множественной регрессии состоит в анализе связи между несколькими независимыми переменными и зависимой переменной при относительно небольшом количестве экспериментов. Экспериментальные данные получены в процессе производства пенобетонных блоков на площадке опытно-экспериментального полигона «Стройкомпозит», г. Якутск.

Цель работы состоит в получении в цеховых (не в лабораторных) условиях достоверных оценок воздействия входных факторов на характеристики пенобетонной смеси и пенобетона при минимальном числе экспериментов.

Материалы и методы исследования

Пенобетонные блоки изготовлены с использованием следующих сырьевых компонентов: в качестве вяжущего – портландцемент класса прочности ЦЕМ I 32,5Б по ГОСТ 31108-2016 и молотая негашеная известь по ГОСТ 9179-2018; в качестве кремнеземистого компонента – механоактивированный кварцполевошпатовый песок из поймы р. Лена по ГОСТ 8736-2014; в качестве воды затворения – техническая вода по ГОСТ 23732-2011; в качестве порообразователя – Foamcem. Образцы размером 100х100х100 мм выпилены из пенобетонных блоков после завершения цикла автоклавной обработки. Физико-механические характеристики пенобетонной смеси и образцов пенобетона определены с использованием стандартных методов и аттестованных приборов лаборатории строительных материалов СВФУ им. М.К. Аммосова. Обработка экспериментальных данных выполнена методами математической статистики на платформах программ STATISTICA и MathCAD.

Результаты исследования и их обсуждение

Рассмотрим технологический процесс изготовления пенобетона как стандартную управляемую систему модели «черного ящика». Наиболее подробно модель «черного ящика» изложена в работах [6, 7]. Система как единый функционирующий «организм» выделена из окружающей среды и в то же время связана с внешними возмущениями от воздействия входных факторов. Система связана со средой посредством входных факторов X = {x1, x2, x3 … xn}, показывающих наблюдаемое влияние среды на систему, посредством возмущающих воздействий, а также выходными данными Y = {y1, y2 … yn}:

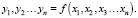(2)

Функцию (2) можно представить в форме линейного уравнения множественной регрессии вида

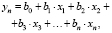(3)

где b0 – свободный член; b1, b2, b3 … bn – коэффициенты регрессии.

Оценка свободного члена и коэффициентов регрессии уравнения (3) производится методом наименьших квадратов [7]:

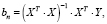(4)

где X – матрица значений входных факторов x1, x2, x3 … xn; XT – транспонированная матрица значений входных факторов x1, x2, x3 … xn; Y – вектор значений выходных данных y1, y2 … yn.

С учетом имеющегося научного задела [4, 8], а также на основании работ других исследователей [2, 3] нами приняты пять рецептурных факторов: x1 – содержание цемента, кг/м³; x2 – содержание извести, кг/м³; x3 – содержание шлама, кг/м³ (50 % массы шлама состоит из механоактивированного песка, остальная часть из воды); x4 – содержание воды, кг/м³; x5 – плотность пены, кг/м³. Рецептурные факторы заданы по расходу необходимого количества материала в кг на 1 м3. Для подбора выходных данных подобран ряд технологических и физико-механических показателей: y1 – расплыв раствора по Суттарду, см; y2 – плотность пенобетонной смеси, кг/м³; y3 – разница температур пенобетона перед резкой и в момент формования, °С; y4 – плотность пенобетона в сухом состоянии, кг/м³; y5 – прочность при сжатии, МПа.

Основной задачей экспериментальных работ является фиксирование условий производственного процесса (входных факторов) с использованием принятой рецептуры пенобетона. Отработанный номинальный состав пенобетонных блоков, кг/м3 [4]: D500: портландцемент – 190, известь – 40, песок – 290, вода – 210; D600: портландцемент – 200, известь – 75, песок – 320, вода – 235 (удельная поверхность песка 350–400 м2/кг). По приведенным составам выполнено сорок замесов (два дублирующих замеса по 20 опытов), где зафиксированы 400 значений входных и выходных данных. Полученные результаты после обработки приведены в таблице. Расход материалов (входные факторы x1 ...x4) показан на один цикл работы пенобетоносмесителя объемом 2,55 м3.

Данные таблицы обработаны с использованием выражения (4), результаты расчетов показаны в уравнениях

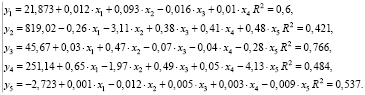(5)

Для оценки адекватности полученных уравнений регрессии применен коэффициент детерминации [7]:

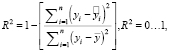(5)

где 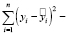сумма квадратов регрессионных остатков; 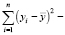общая дисперсия; 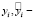фактические и расчетные значения выходных данных;

Чем ближе коэффициент детерминации к единице, тем лучше и адекватнее модель приближает рассчитанные по уравнениям (5) значения к наблюдаемым экспериментальным данным (таблица). Коэффициенты детерминации уравнений регрессии также приведены в (5). При оценке корреляционной связи между входными и выходными данными необходимо исключать уравнения, у которых R2 < 0,5, соответственно, y2 и y4 в дальнейших расчетах не учитываем.

Составленные уравнения множественной регрессии (5) являются линейными моделями, описывающими наклонную гиперплоскость в факторном пространстве. Исходя из этого, если не принимать ограничения, то, анализируя модель, можно получить недостоверные данные. Поэтому в расчетах учитывается только та локальная область факторов, которая была изучена в ходе проведения экспериментальных работ (таблица), а именно:

;

;

;

.

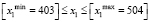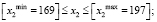
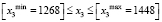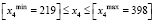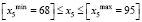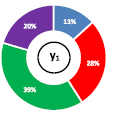
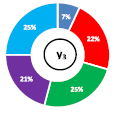
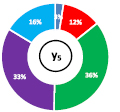
Следующим этапом является анализ уравнений y1, y3 и y5 по принципу Парето. Для этого применили специальный инструмент программы STATISTICA «график Парето». Полученные в результате анализа принципа Парето данные иллюстрированы в виде круговых диаграмм и показаны на рисунке.

Анализ диаграмм показывает, что наибольшее влияние на степень изменчивости всех трех выходных данных оказывает фактор x3 – содержание шлама. Для расплыва раствора по Суттарду на втором месте по силе влияния оказалось содержание извести x2 = 28 %. Расплыв по своей природе показывает реологию растворной составляющей, поэтому наличие в нем шлама и извести повышает его растекаемость. Это связано с тем, что шлам отчасти состоит из воды, а известь после гашения придает смеси пластичность. Однако стоит отметить и роль воды затворения x4 = 20 %, который занимает третью строчку по силе влияния на y1. Следует отметить, что факторы x3 и x4 производят некоторый синергетический эффект, который повышает суммарное содержание водной составляющей, тем самым увеличивая пластичность растворной смеси. Для перепада температур y3, так же как и у y1, наибольший вклад вносит x3 и только потом x5 = 25 % и x2 = 22 %. Такое ранжирование отчасти противоречит общепринятым принципам, то есть с увеличением количества извести, температура пенобетонного массива должна пропорционально увеличиваться (за счет взаимодействия СаО с Н2О). Возможно, это связано с особенностями морфологии воздушных пузырьков пенобетона, так как структура всех ячеистых бетонов напрямую зависит от характеристик порообразователя, в данном случае – плотности пены x5. Изменчивость y5 показала довольно-таки прогнозируемый результат, характеризуемый для большинства бетонов на основе вяжущих гидратационного твердения. На прочность при сжатии y5 наибольшее влияние оказывают x3 = 36 % и x4 = 33 %, так как их повышенное содержание увеличивает водовяжущее отношение и, как следствие, ухудшение прочностных показателей. Установлено, что на прочность при сжатии существеннее влияние оказывает плотность пены x5 = 16 %, чем содержание цемента или извести по отдельности. Это доказывает известную гипотезу, что для пенобетона главную роль в структурообразовании занимают тип и характеристики пены, а не расход вяжущего (в рассмотренных плотностях). Доминирующая роль фактора x3 на изменчивость всех выходных данных объясняется тем, что он занимает порядка 55 % всех вместе взятых исходных компонентов пенобетона (по массе). Таким образом, от колебания фактора x3 наблюдается сильная вариативность рассматриваемых выходных данных y1, y3 и y5.

Заключение

Переносить полученные результаты на другие типы ячеистых бетонов следует с достаточной осторожностью, наиболее подходящими являются пенобетоны автоклавного твердения с похожим диапазоном распределения плотностей. Тем не менее выявленные зависимости не противоречат известным зависимостям, а некоторые данные подтверждают ранее не рассматриваемые среди исследователей подходы и идеи. Следует отметить, что математические модели, полученные на основе уравнений регрессии, в большинстве случаев применяются только для описания поверхности отклика, а с использованием уравнения множественной регрессии в тандеме с принципом Парето можно более подробно анализировать исследуемые процессы и явления. Исследование планируется продолжить в области анализа нелинейных уравнений регрессии при моделировании технологических процессов изготовления ячеистых бетонов с более широким охватом средней плотности.