Производство высококачественной продукции легкой промышленности, способной обеспечить конкурентное преимущество на современном динамически развивающемся рынке, невозможно без внедрения инноваций и цифровизации отрасли в целом. Одним из направлений инновационного развития легкой промышленности является внедрение нанотехнологий, которые позволяют получить продукцию с улучшенными гигиеническими и эксплуатационными свойствами. Результаты научных работ в данном направлении изложены в работах [1–3]. В настоящее время проводится ряд исследований мирового уровня по исследованию модифицированных наночастицами металлов, в том числе серебра, образцов методами рамановской спектроскопии, а также по распознаванию наночастиц на различных текстильных объектах: волокнах, трикотажных, нетканых материалах, тканях. При этом актуальной задачей является повышение точности идентификации наночастиц металлов с целью дальнейшего контроля режимов нанесения на различных технологических переходах. Решение данной задачи невозможно без внедрения автоматизированных систем управления и контроля технологическими процессами производства изделий легкой промышленности. Разработка таких систем должна базироваться на математическом аппарате, реализованном с помощью современных компьютерных систем [4; 5].
В работах [6; 7] рассмотрены разработанные авторами методы идентификации наночастиц на текстильных материалах и их программная реализация. К недостаткам данных методов можно отнести недостаточную точность, необходимость подбора значений плотностей вероятностей вручную, что занимает длительное время и значительно увеличивает трудоемкость решения задачи.
Для повышения точности необходимо разработать метод автоматического решения систем уравнений параметров, по которым будет осуществляться идентификации наночастиц.
Цель работы: разработка программной реализации математической модели распознавания наночастиц серебра на поверхности текстильных материалов.
Материалы и методы исследования
Для исследования выбраны полиэфирные волокна, обработанные наночастицами серебра. Исследование характеристик полученных образцов проводилось с использованием методов рамановской спектроскопии. На сканирующем зондовом микроскопе в региональном центре нанотехнологий ЮЗГУ были получены рамановские спектры волокон полиэфира, с наночастицами серебра и без них. На каждом образце проведены пять измерений в различных точках с поперечной (Х) и продольной (Y) поляризацией лазерного луча.
В математическом редакторе Math-CadEdition 15 были определены математические ожидания и средние квадратические отклонения интенсивности для девяти основных пиков рамановских спектров с поперечной (Х) и продольной (Y) поляризацией без наночастиц и с наночастицами серебра соответственно: mX, mXAg, mY, mYAg, sX, sXAg, sY, sYAg.
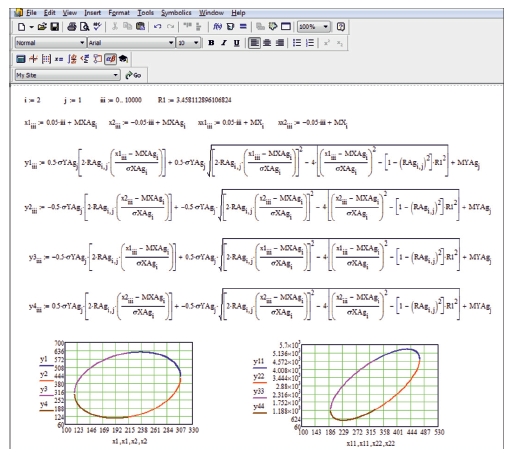
Рис. 1. Фрагмент программы построения эллипсов распределения интенсивностей излучения рамановских спектров
Авторами для оценки точности идентификации наночастиц серебра на волокнистых материалах предлагается использовать дифференцирование по X и Y одновременно по плотности вероятностей пересечения эллипсов распределения высоты пиков рамановского поляризационного спектра в векторно-матричных аналитических выражениях: ln(p) = X0 T×R0-1×X0 и ln(pAg) = XAgT×RAg-1×XAg для p и pAg. Для построения эллипсов распределения для соответствующих пиков рамановских спектров без наночастиц и с нано-частицами серебра была разработана программная реализация в математическом редакторе MathCad, фрагмент которой представлен на рис. 1.
Графическая оценка пересечения эллипсов распределения рамановских спектров, полученная с использованием предложенной программы для различных пиков, представлена на рис. 2.
В основу метода положено определение плотностей вероятностей (p и pAg) по точкам пересечения эллипсов распределений рамановских спектрограмм. Для проведения аналитической оценки p и pAg в данной работе авторами предложен метод с использованием векторно-матричного анализа 1-3.
Особенностью предложенного метода является то, что решение системы осуществляется автоматически без ручного подбора значений параметра p. При этом в системе (3) выражение g(x,y) представляет двойную производную Якобиана (по dx и по dy), а в выражении f(x,y) отсутствует дифференцирование.
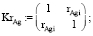
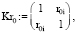 (1)
(1)
где r0, rAg – корреляционные матрицы рамановских поляризационных спектров полиэфирных волокон без наночастиц и с наночастицами серебра.
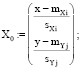
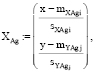 (2)
(2)
где i, j – номера пиков спектрограмм, пресечение которых исследуется.
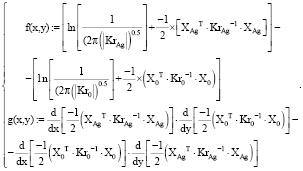 (3)
(3)
Результаты исследования и их обсуждение
Программная реализация нахождения решения системы уравнений (3) была осуществлена с применением функционала математического редактора MathCad Enterprise Edition 15, фрагмент которой для исследования пересечения 4 и 3 пиков представлен на рис. 3.
Таким образом, результатом решения системы уравнений (3) в программе MathCad является вектор v, содержащий координаты пересечения эллипсов распределения рамановских спектров волокон с наночастицами и без наночастиц.
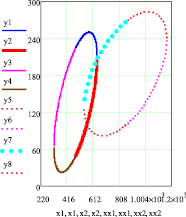
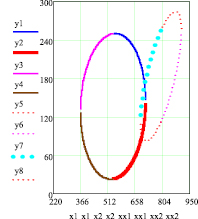
а) б)
Рис. 2. Графическая оценка пересечения эллипсов рамановского спектра: а) для 6 и 8 пиков; б) для 9 и 7 пиков
Для определения плотности вероятностей точек пересечения эллипсов распределения интенсивностей переизлучения рамановских спектров р0 для уравнения без наночастиц и рAg для уравнения с наночастицами серебра при условии одновременного дифференцирования по Х и по Y используются выражения (4–5).
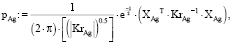 (4)
(4)
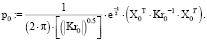 (5)
(5)
При этом в качестве переменных x и y подставляются результаты решения системы дифференциальных уравнений – значения вектора v.
Значения достоверности р0 и рAg, определенные по выражениям (4–5), программная реализация которых также представлена на рис. 3
– при исследовании пересечения 6 и 8 пиков спектрограмм:
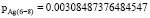
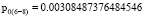
– при исследовании пересечения 9 и 7 пиков спектрограмм:
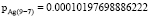
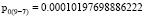
– при исследовании пересечения 7 и 5 пиков спектрограмм:
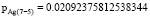
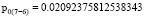
– при исследовании пересечения 2 и 4 пиков спектрограмм:
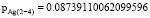
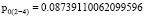
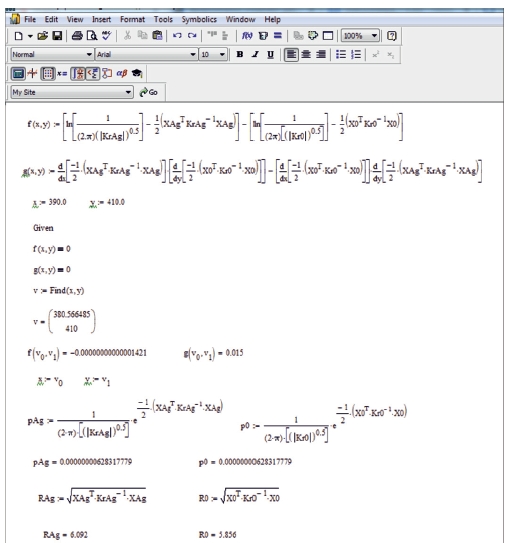
Рис. 3. Фрагмент программной реализации решения системы уравнений
Значения p с соответствующим числом знаков формируются программой автоматически. Оценку точности производим по совпадению численных значений после запятой. Анализ результатов дает основание сделать вывод, что р и рAg для соответствующих пиков либо равны, либо практически равны. По методу, предложенному в предыдущих исследованиях, изложенных в том числе в работе [7], для обеспечения точности 10-15–10-16 в уравнения необходимо было вводить величину D, подбираемую в ручном режиме. Разработанный авторами метод в данной работе позволяет получать решение автоматически, при этом точность повышается до 10-17.
На основании решения системы уравнений (3) для точек пересечения по выражениям 6-7 вычисляются радиусы кривизны эллипсов распределения интенсивности излучения рамановских спектров. При этом R – радиус эллипса для рамановских спектров без наночастиц; RAg – радиус эллипса для рамановских спектров с наночастицами серебра.
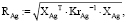 (6)
(6)
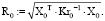 (7)
(7)
При этом значения RAg и R0 для эллипсов распределения рамановских спектров при пересечении 9 и 7 пиков получились следующие:
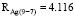
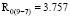
Выводы
На основании проведенных исследований и математической обработки их результатов можно сделать вывод, что предложенный авторами метод использования системы дифференциальных уравнений в векторно-матричном виде (3) дает высокую точность результатов. При этом численное решение в большом диапазоне задания начальных параметров получается автоматически.
Полученные решения системы уравнений по определению координат пересечения эллипсов распределения имеют высокую точность и не зависят от начального значения параметров х и у в указанном диапазоне.
В результате математической обработки результатов исследований выявлена точность идентификации наночастиц серебра. Так, для 6 и 8 пиков:
p0 = 0.00308487376484546
и
pAg = 0.00308487376484547
и для 7 и 5 пиков:
p0 = 0.02092375812538343
и
pAg = 0.0209375812538344
можно оценить до 10-17.
Более высокую точность не дает ни один из исследуемых методов.
Для совершенствования предложенного метода необходимо построение и решение системы дифференциальных уравнений с количеством неизвестных параметров более двух при дифференцировании совместно по двум переменным, оценка точности идентификации наночастиц серебра на текстильных материалах при использовании многомерного дифференцирования с исследованием двух и более пиков рамановского спектра.



