В современном строительстве широко и многофункционально используются многослойные пластины. Слои пластин выполняют как из новых, так и традиционных материалов, в том числе композитных. Эти материалы в основном характеризуются свойством разномодульности, то есть имеют различные модули упругости при растяжении и сжатии [1]. Решая задачи изгиба составных конструкций, необходимо учитывать особенности их деформирования в реальных условиях за счёт взаимного проскальзывания слоёв. Перераспределение усилий между слоями обеспечивается переменной жёсткостью швов. При расчёте напряжённо-деформированного состояния необходимо учитывать влияние жёсткости межслойных связей. Построение математической модели подробно изложено в [2].
Цель исследования: математическая модель изгиба многослойных составных пластин из разномодульных материалов включает систему дифференциальных уравнений и граничные условия. В результате интегрирования уравнений равновесия, неразрывности и работы шва, искомые функции W, φi, Ti должны удовлетворять краевым условиям, которые соответствуют конкретному закреплению контура.
Материалы и методы исследования
Построение математической модели и последующие исследования выполнялись методами математического моделирования.
Результаты исследования и их обсуждение
Рассматривается изгиб составных пластин, у которых материал среднего слоя имеет различные модули Юнга на растяжение и сжатие, определяющим является знак главного напряжения [3], разномодульность связана с положением главных площадок [4]. Рассмотрим составную трехслойную симметричную пластину. Размеры пластины 1200×1200 мм. Толщины крайних стальных листов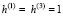 
мм, общая толщина 120 мм. Модули упругости 
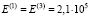МПа; 
МПа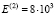, коэффициенты Пуассона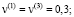 
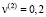. Нагрузка интенсивностью q = 1 МПа прикладывалась в центре пластины на площадке 200×200 мм по нормали.
Слои в составной пластине соединены связями, которые предполагают сдвиг одного слоя по отношению к другому вдоль оси пластин. Поперечные связи абсолютно жесткие. Такое соединение слоев обеспечивает одинаковый прогиб.
Интегральные характеристики жесткости для i-го слоя составной пластины запишем с учётом разномодульных свойств материала [1], в декартовых координатах. Переход от направлений главных площадок к координатам X, Y осуществляем через преобразование матрицы податливостей, в отличие от [5].
Математическую модель изгиба составной конструкции из разномодульных материалов запишем в виде системы дифференциальных уравнений [1]. Стремясь к смешанной форме уравнений, введем в рассмотрение функцию усилий φ(x, y), действующих в срединной поверхности i-го слоя. Запишем усилия, действующие в i-м слое:
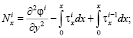
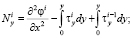(1)
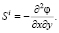
Обозначим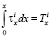 
, 
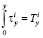, где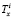 
, 
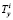– усилия от сдвигающих напряжений в межслойных связях i-го шва.
Уравнение равновесия получим из рассмотрения элемента i-го слоя пластины в смешанном виде [1]:
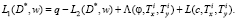(2)
Уравнение неразрывности для срединной поверхности i-го слоя в операторной форме [1]:
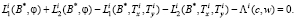(3)
Чтобы замкнуть систему, запишем уравнения, отражающие работу i-го шва. В этих уравнениях учитывается совместная работа слоев, прилегающих к i-му шву.
В каждом шве выделим осевую линию, по обе стороны которой происходят продольные смещения слоев. Разности этих смещений запишутся как
; 
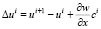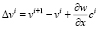, (4)
где ui(x, y), vi(x, y), wi(x, y) – продольные и поперечные смещения точек серединной поверхности i-го слоя; ci(x, y) – расстояние между серединными поверхностями смежных слоев, при переменной толщине слоев.
Связь между Δui, Δvi и сдвигающими напряжениями в i-м шве представим в виде [2]:
Напряжения сдвига записываются через функци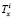и 
и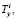 
учитывающие работу i-го шва:
; 
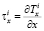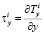. (5)
Выразим из (5) Δui, Δvi, подставим их в (4). Продифференцируем первое уравнение (4) по x, второе по y. Запишем полученные уравнения [1]:
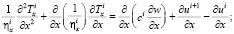
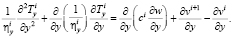(6)
Математическая модель изгиба многослойных составных пластин из разномодульных материалов состоит из системы дифференциальных уравнений и граничных условий.
В результате интегрирования (2), (3) и (6) искомые функции W, φi и Ti должны удовлетворять краевым условиям, которые соответствуют конкретному закреплению контура.
В общем случае можно выделить две группы граничных условий: на контуре опирания (для всего пакета) и на торцах пакета (для каждого i-го слоя и шва). При этом условия на контуре формулируются независимо от условий на торцах слоев и швов.
Варианты опирания на контуре:
1. Шарнир.
2. Жесткая заделка.
3. Свободный край.
Условия на торцах слоев:
A – торцы слоев скреплены гибкой лентой;
B – торцы скреплены абсолютно жесткой лентой;
C – свободные торцы.
Полагая, что на всех четырех кромках составной пластины условия одинаковы, приступим к рассмотрению случаев опирания по кромкам x = 0 и x = a:
1 – A. Пластина опирается на шарнир, подвижный по нормали к контуру и неподвижный вдоль контура, а торцы слоев скреплены гибкой лентой. Граничные условия имеют вид
W = 0; V i = 0; Mx = 0;
; 
; 
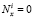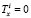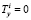. (7)
Из первого условия следует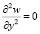 
. Из (1), если 
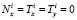, то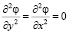 
. Из (7) искомые функции, должны удовлетворять следующим условиям:
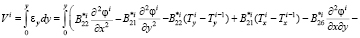
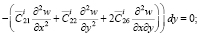
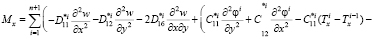(8)
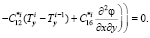
1 – B. При шарнирном опирании пластины торцы скреплены абсолютно жесткой лентой. Граничные условия имеют вид
W = 0; Ui = 0; Vi = 0;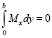 
; 
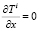. (9)
Так как W принимает на кромке нулевое значение, то и производная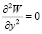 
вдоль этой кромки.
Распишем условия (9):
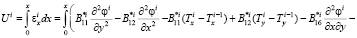(10)
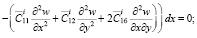
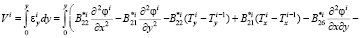
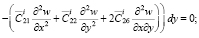
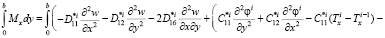
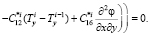
Далее система (9) расписывается относительно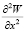 
, 
, 
.
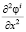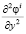1 – C. Составная пластина со свободными торцами слоев опирается на шарнир. Краевые условия для этого случая:
W = 0; Mx = 0;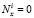 
; Si = 0; Ti = 0. (11)
Равенство нулю прогиба на кромке приводит к условию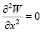 
, 
.
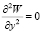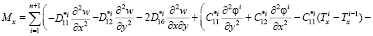
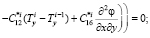
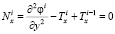; (12)
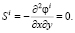
Окончательно получим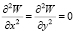 
;
Ti = 0;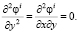 
(13)
Заключение
Представленные дифференциальные уравнения позволяют решать, в отличие от существующих моделей, задачи изгиба многослойных пластин из разносопротивляющихся материалов с учетом влияния жесткости межслойных связей на напряженно-деформированное состояние конструкции. Свойство разномодульности материала учтено при записи интегральных характеристик жесткости. Тот факт, что дифференциальные уравнения имеют высокий порядок, позволяет учитывать сложные и разнообразные кинематические и статические условия закрепления слоев оболочки. Граничные условия для функции, которая отражает условия, связанные с внешней статической неопределимостью, должны записываться для каждого слоя, для функции, отвечающей за внутреннюю статическую неопределимость конструкции, для каждого шва.