При принятии логистических решений компаниям, занимающимся транспортировкой некоторой продукции, требуется решать задачи так называемого операционного уровня. Одними из таких задач являются задачи поиска рациональных маршрутов различными транспортными средствами маршрутизации (VRP) [1]. Существует множество различных постановок таких задач, которых объединяет, прежде всего, наличие парка транспортных средств (депо) и клиентов, спрос которых необходимо удовлетворить. При этом любой искомый маршрут должен начинаться и заканчиваться в депо, задана матрица неотрицательных стоимостей (расстояний) между клиентами. Необходимо определить такой маршрут доставки заказов автомобильными транспортными средствами всем клиентам, чтобы общие затраты были минимальными. Известны различные постановки задач маршрутизации с ограничениями, которые встречаются при решении реальных задач. Целью исследования является решение практической задачи маршрутизации с возможностью дозагрузки недостающего груза в специализированных пунктах с предварительным размещением груза в автомобильные транспортные средства (решается задача трехмерной упаковки, 3DBPP).
Постановка задачи и математическая модель
В статье рассматривается задача маршрутизации для доставки груза различным клиентам с возможностью дозагрузки и его размещения в автомобильные транспортные средства (MVRPSF), в основу которой легли следующие известные задачи [2–4]: задача маршрутизации с учетом вместимости транспортного средства (CVRP); задача маршрутизации с условием обслуживания клиентов одновременно несколькими транспортными средствами (SDVRP); задача маршрутизации с возможностью дозагрузки груза в специализированных пунктах или депо (VRPSF).
Задача маршрутизации MVRPSF возникла в компании, занимающейся доставкой оборудования для установки освещения в различных регионах России арендуемыми автомобильными транспортными средствами одинаковой вместимости, находящимися в депо. На пути следования к клиентам имеются пункты дозагрузки, в которых автомобильные транспортные средства могут пополнять недостающий запас оборудования, не возвращаясь в депо. Известны данные о спросе клиентов на оборудование, о времени обслуживания клиентов (населенные пункты), о максимально разрешенном времени маршрута, о стоимости в единицу времени пройденного пути автомобильного транспортного средства (в стоимость входят стоимости аренды и бензина). Следует найти маршрут доставки оборудования с минимальными общими затратами при выполнении следующих условий: все пути для доставки груза начинаются в депо; после выполнения заказов автомобильные транспортные средства должны возвратиться обратно в депо; весь объем груза, доставляемого различным клиентам, не должен превосходить вместимости транспортных средств (CVRP); требования клиентов на поставку груза разделяются между несколькими транспортными средствами (SDVRP).
В задаче MVRPSF маршруты между клиентами представляются в виде графа. Вершины графа разбиваются на два непересекающихся множества, одно из которых I – множество клиентов (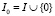 , где вершина 0 – это депо; i, j – номера клиентов;
, где вершина 0 – это депо; i, j – номера клиентов; 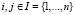 ); другое множество F – это пункты дозагрузки; α – индекс, используемый для описания пунктов дозагрузки или депо,
); другое множество F – это пункты дозагрузки; α – индекс, используемый для описания пунктов дозагрузки или депо, 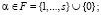 Fα – множество вершин, соответствующее потенциальным посещениям пунктов дозагрузки; F0 – депо, используемое в качестве пункта для дозагрузки; nα – количество дополнительных пунктов для дозагрузки;
Fα – множество вершин, соответствующее потенциальным посещениям пунктов дозагрузки; F0 – депо, используемое в качестве пункта для дозагрузки; nα – количество дополнительных пунктов для дозагрузки; 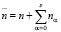 – количество пунктов в сети; dij – расстояние либо между клиентами i и j, либо между клиентами и депо, либо между дозагрузочными пунктами; τij – время в пути между пунктами i и j; m – количество используемых транспортных средств; Qv – вместимость транспортных средств v;
– количество пунктов в сети; dij – расстояние либо между клиентами i и j, либо между клиентами и депо, либо между дозагрузочными пунктами; τij – время в пути между пунктами i и j; m – количество используемых транспортных средств; Qv – вместимость транспортных средств v; 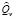 – максимальное количество разрешенного в транспортном средстве v остатка груза до его пополнения,
– максимальное количество разрешенного в транспортном средстве v остатка груза до его пополнения, 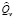 < Qv; cos trent – стоимость аренды транспортного средства в единицу времени; cos tpetrol – затраты на бензин транспортного средства; Tv – максимально разрешенное время маршрута для транспортного средства v; qi – спрос клиента i; piv – время обслуживания клиента i транспортным средством v время загрузки в дозагрузочных пунктах, либо в депо.
< Qv; cos trent – стоимость аренды транспортного средства в единицу времени; cos tpetrol – затраты на бензин транспортного средства; Tv – максимально разрешенное время маршрута для транспортного средства v; qi – спрос клиента i; piv – время обслуживания клиента i транспортным средством v время загрузки в дозагрузочных пунктах, либо в депо.
В качестве решения выступает xvij – переменная, принимающая значение 1, если автомобиль v перемещается из депо в направлении от клиента i к клиенту j, и 0 в противном случае. Используемые переменные: 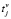 – время начала обслуживания клиента j; yjv – загрузка остатка заказанного груза непосредственно перед посещением клиента j;
– время начала обслуживания клиента j; yjv – загрузка остатка заказанного груза непосредственно перед посещением клиента j; 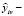 количество заказа, доставляемого клиенту i автомобилем v;
количество заказа, доставляемого клиенту i автомобилем v;
Математически задача MVRPSF формулируется следующим образом [5]
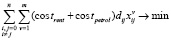 (1)
(1)
при следующих ограничениях:
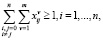 (2)
(2)
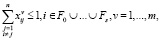 (3)
(3)
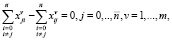 (4)
(4)
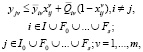 (5)
(5)
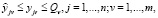 (6)
(6)
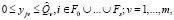 (7)
(7)
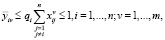 (8)
(8)
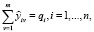 (9)
(9)
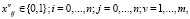
где
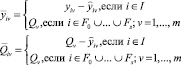
Приведем известные постановки задач CVRP и SDVRP, условия которых применялись в задаче MVRPSF.
Требуется найти маршрут минимальной стоимости (CVRP):
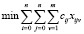 (10)
(10)
при выполнении следующих условий:
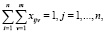 (11)
(11)
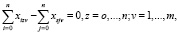 (12)
(12)
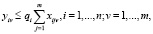 (13)
(13)
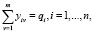 (14)
(14)
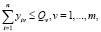 (15)
(15)
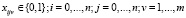 ;
;
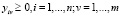 .
.
В задаче SDVRP при поиске маршрута минимальной стоимости (10), кроме условий (12)–(15), используются следующие условия:
маршрут включает каждую вершину не менее одного раза:
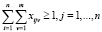 (16)
(16)
исключаются замкнутые маршруты:
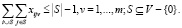 (17)
(17)
Для решения задачи MVRPSF с учетом перечисленных условий (11)–(17) был разработан алгоритм VRPSF на базе эволюционной стратегии 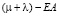 [4], который находит рациональный маршрут доставки грузов и осуществляет их предварительное размещение в кузове автомобильных транспортных средств с учетом центра тяжести размещаемых грузов (решается задача трехмерной упаковки 3DBPP [6]).
[4], который находит рациональный маршрут доставки грузов и осуществляет их предварительное размещение в кузове автомобильных транспортных средств с учетом центра тяжести размещаемых грузов (решается задача трехмерной упаковки 3DBPP [6]).
Для применения алгоритма VRPSF следует определиться с кодировкой решения – маршрута, начинающегося и заканчивающегося в депо. В данном алгоритме кодировка искомого решения – маршрута представляется в виде перестановки целых чисел 1,...,n. Приведем общую схему алгоритма VRPSF решения задачи (1)–(9).
Общая схема алгоритма VRPSF
Шаг 0. Инициализация переменных
Шаг 1. Загрузка груза в ТС v (решается 3DBPP)
Шаг 2. Цикл по количеству итераций
Если маршрута нет, то генерировать λ маршрутов 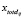
иначе
Цикл по λ
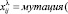
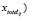
Конец_цикла_по_λ
Конец_ если_маршрута_нет
Цикл по количеству маршрутов
K = Qv (решается 3DBPP)
Цикл по количеству клиентов n
Пока спрос i-го клиента qi не будет удовлетворен, выполнить:
Если в автомобиле v все грузы i-го клиента размещены (т.е. спрос
qi ≤ K),
то спрос i-го клиента удовлетворен
иначе
Если qi > Qv, то
Поиск ближайшего пункта дозагрузки от клиента
иначе
Поиск наименьшего расстояния до пункта
дозагрузки и от пункта дозагрузки до следующего клиента
Конец _Если
Если найденный пункт дозагрузки депо и если есть
незадействованные автомобили,
то новый автомобиль вводится в маршрут
Добавление найденного пункта дозагрузки в маршрут
K = Qv (решается 3DBPP)
Конец_если
Конец_цикла_пока
Конец цикла по количеству клиентов
Конец_цикла_по_количеству_маршрутов
Если выполняются ограничения (1)-(9), то сравнение стоимости
нового и текущего маршрутов и выбор наилучшего маршрута,
иначе маршрут не существует
Конец_цикла_по_итерациям
Вывод маршрута 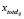 и получение карты размещения грузов в ТС
и получение карты размещения грузов в ТС
Численные результаты
Для исследования эффективности разработанного алгоритма VRPSF проводились численные эксперименты. При этом в основу реализации алгоритма VRPSF были положены эволюционные стратегии (1 + 3)-ЕА и (1 + 4)-ЕА [7]. Приведем результаты одного из экспериментов, для которого были сгенерированы тестовые наборы данных: расстояния между клиентами, между клиентами и пунктами дозагрузки, величины спроса соответственно для 20 клиентов, пункты дозагрузки варьировались от 1 до 5. В тестовом наборе данных Kn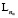 Eq обозначение Kn – это количество клиентов (n = 20);
Eq обозначение Kn – это количество клиентов (n = 20); 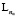 – количество пунктов дозагрузки (nα = 0,..,5); Eq – количество прогонов (q = 7); 400I и 500I – количество итераций алгоритмов. Каждый тестовый набор прогонялся семь раз. В таблице приведено сравнение средних стоимостей маршрутов для 20 клиентов и пяти дозагрузочных пунктов лишь для количества итераций 400I, на рисунке, а, б, приведены диаграммы для результатов таблицы и среднего времени работы алгоритмов (1 + 3)-EA и (1 + 4)-EA для 400I и 500I.
– количество пунктов дозагрузки (nα = 0,..,5); Eq – количество прогонов (q = 7); 400I и 500I – количество итераций алгоритмов. Каждый тестовый набор прогонялся семь раз. В таблице приведено сравнение средних стоимостей маршрутов для 20 клиентов и пяти дозагрузочных пунктов лишь для количества итераций 400I, на рисунке, а, б, приведены диаграммы для результатов таблицы и среднего времени работы алгоритмов (1 + 3)-EA и (1 + 4)-EA для 400I и 500I.
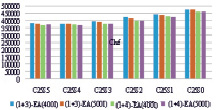
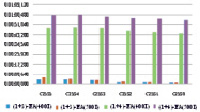
а) б)
Диаграммы для результатов таблицы и среднего времени работы алгоритмов (1 + 3)-EA и (1 + 4)-EA для 400I и 500I: а) cравнение средних стоимостей маршрутов; б) среднего времени работы алгоритмов для 20 клиентов
Как показали численные эксперименты, лучший результат показал алгоритм (1 + 4)-EA, алгоритм (1 + 3)-EA затрачивает меньше вычислительного времени, при этом на стоимость маршрута оказывает влияние количество пунктов дозагрузки: она меньше при их количестве, равном пяти (в данном эксперименте).
Сравнение средних стоимостей маршрутов для 20 клиентов
|
(1 + 3)-ЕА(400I) |
(1 + 4)-ЕА(400I) |
|
|
K25L5 |
3778,518 |
2673,211 |
|
K25L4 |
3654,789 |
2565,561 |
|
K25L3 |
3586,780 |
3335,722 |
|
K25L2 |
4063,111 |
3909,575 |
|
K25L1 |
4256,881 |
4034,111 |
|
K25L0 |
4733,366 |
4583,175 |
Заключение
В представленной статье рассмотрена практическая задача маршрутизации с возможностью дозагрузки и приведены ее математическая модель и алгоритм, позволивший получить рациональный маршрут доставки грузов клиентам с возможностью дозагрузки и с предварительным размещением их в ТС, который базируется на эволюционных стратегиях (1 + 3)-EA и (1 + 4)-EA. Для проведения численного эксперимента были сгенерированы тестовые наборы данных для 20, 25, 30, 35 и 40 клиентов. В статье приведены результаты численных экспериментов для 20 клиентов, при этом лучшие по целевой функции решения были получены алгоритмом (1 + 4)-EA.
Работа поддержана грантом РФФИ 18-07-00193-а.



