Для отображения в полной мере реальных физических процессов накопления повреждений в материале при механических испытаниях рекомендуется использовать полностью равновесные диаграммы деформирования (ПРДД), полученные при испытаниях на изгиб [1].
Цель исследования: предложить математическую модель описания полной равновесной диаграммы деформирования, применение которой поможет исключить проведение сложных равновесных опытов.
Образцы из шлакобетона, испытание на изгиб.
Так как для определения характеристик трещиностойкости бетона (вязкости разрушения) при статическом нагружении используют диаграмму «нагрузка – прогиб» («F – f») [1], равно как и диаграмму «напряжения – относительные деформации» («s – e») в теории бетонных и железобетонных конструкций [2–4], разработка методов их математического описания является по-прежнему актуальной задачей механики твердого тела, в частности механики строительных композиционных материалов. При множестве предложенных зависимостей проблема здесь заключается к сведению к минимуму параметров уравнений.
Для математического описания зависимости приложенной нагрузки (F) от прогиба (f) при трехточечном изгибе примем в качестве характерных параметров диаграммы «F – f» следующие параметры (рис. 1): угол наклона восходящей ветки диаграммы к оси абсцисс α (tg α = 0,6Fc/f1), точка 1 окончания прямолинейного участка восходящей ветки, точка 2 вершины кривой деформирования, точка 3 перегиба ниспадающей ветви диаграммы и точка 4 дефрагментации образца.
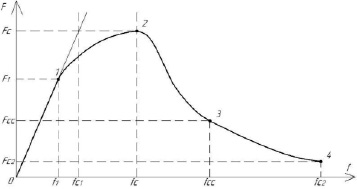
Рис. 1. Параметрические точки диаграммы «нагрузка – прогиб»
Предлагается математическое описание диаграммы «F – f» в следующем виде:
F(f) = AfB?eCf, (1)
в котором А, В и С – параметры кривой деформирования
Параметры А, В и С уравнения (1) находим исходя из физических и геометрических соображений, а также на основе полученных экспериментальных данных
Будем считать, что отрезок изменения величины прогиба f от точки f = 0 к точке fc, в которой функция F(f) получает максимальное значение, отвечает почти линейному закону изменения усилия F от прогиба f.
Учитывая это, примем, что параметр A является известным. В первом приближении он будет равен значению производной от функции F(f) по параметру f в некоторой точке промежутка прямолинейного изменения усилий F. Следовательно,
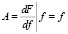, (2)
т.е. параметр А будет равен тангенсу угла наклона восходящей ветки диаграммы в области упругих деформаций к оси Of системы координат FOf.
Вычислим производную:
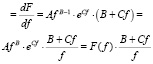, (3)
которая равна нулю при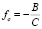 
.
Тогда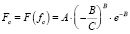 
или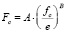 
, и отсюда следует,что
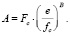(4)
Для упругого материала можно допустить, что
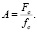(5)
Из отношений (4) и (5) определим параметр B из равенства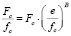 
, откуда
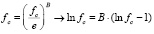
и
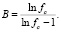(6)
Тогда из соотношения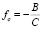 
находим
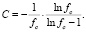(7)
После постановки параметров А, В и С в соотношении (1) получаем
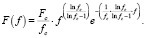(8)
В качестве примера возьмем следующие данные: Fc = 3500 Н, fc = 0,09 мм, при которых искомые параметры диаграм- мы деформирования принимают значения А = 38,9* 103 Н/мм, В = 0,71 и С = –7,851 м-1.
С их использованием по формуле (1) с учётом экспериментальных значений Fc и fС по формуле (8) на рис. 3 построена полная диаграмма «F – f».
Использование диаграмм деформирования ПРДД для расчета железобетонных конструкций на основе отходов различных отраслей промышленности и местных заполнителей, в частности – шлакобетона, получаемого на основе шлаковой пемзы [5, 6], является также актуальной задачей.
Однако, как показали опыты, диаграмма деформирования, описываемая формулой (1) для упруго-пластичного материала (рис. 2), отличается от реальной диаграммы на нисходящей ветви при испытании шлакобетонного образца. Это объясняется тем, что после достижения нагрузкой своей максимальной величины происходит лавинное трещинообразование (в нашем случае – начало и дальнейшее динамическое движение магистральной трещины).
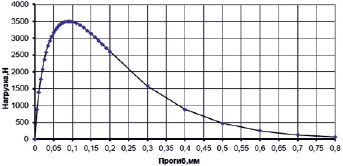
Рис. 2. Диаграмма деформирования «F-f», построенная по формуле (8)
В таблице приведены сравнительные значения параметрических точек ПРДД, полученных по формуле (8) и из экспериментальной диаграммы деформирования прямоугольного образца из мелкозернистого шлакобетона возрастом 714 суток, призменная прочность – 45 МПа, прочность при изгибе – 10,42 МПа (серия ОА-0-0-6(10-12-02) с размерами поперечного сечения 40х40 мм, длина пролета L = 150 мм, момент инерции I = 213333,33 мм4).
Значения параметров ПРДД
|
Параметры ПРДД |
Точка «1» |
Точка «2» |
Точка «3» |
Точка «4» |
||||
|
F1 = 0,6 Fс , Н |
f1 = 0,6fс1, мм |
Fс, Н |
fс, мм |
Fсс, Н |
fсс = 2fс, мм |
Fс2, Н |
fс2 = 6fс2, мм |
|
|
опытные |
2100 |
0,02 |
3500 |
0,09 |
2200 |
0,18 |
150 |
0,54 |
|
по ф-ле (8) |
2100 |
0,02 |
3500 |
0,09 |
2850 |
0,18 |
400 |
0,54 |
Как видно из таблицы, на нисходящем участке наблюдается расхождение опытных и теоретических (8) значений приложенной нагрузки, поэтому необходимо внести корректировку в формулу(8) с учетом динамического движения магистральной трещины.
При расчете железобетонных конструкций по деформациям на основе нелинейной деформационной модели (НДМ) используется модуль деформаций (секущий или касательный), который, в отличие от начального модуля упругости (Еb – постоянная величина), с возрастанием величины и длительности действия нагрузки меняется по величине и, падая, стремится к нулю, а деформации достигают своих предельно максимальных значений [1, 2, 6].
Значение начального модуля упругости можно получить из опытов на сжатие или при измерении скорости ультразвука в материале, либо непосредственно при изгибе [1, 3, 7].
Математическая модель на основе одного параметра (максимальное значение силы). Покажем в дальнейшем, что математически можно описать диаграмму деформирования материала при изгибе через один параметр Fc (максимальное значение нагрузки), учитывая, что модуль упругости известен.
Представим выражение (1) в следующем виде:
F(f) = AfeBf, (9)
в котором А и В – параметры кривой деформирования.
Параметр A является известным и равен тангенсу угла наклона восходящей ветки диаграммы (рис. 1) в области упругих деформаций к оси Of системы координат FOf (А = Fс/fc1 = F1/f1 = 0,6 Fс/0,6fc1).
Вычислим производную:
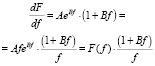, (10)
которая равна нулю при 
.
Тогда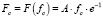 
, и отсюда следует, что
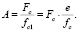(11)
Из отношений (11) определим параметр
fc = 2,718fc1. (12)
Начальный модуль упругости при изгибе равен [5]:
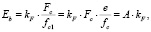(13)
где kF – единичная податливость при трехточечном изгибе, равная kF = L3/(48I) (для опытного образца серии ОА-0-0-6(10-12-02) с размерами поперечного сечения 40х40 мм, длина пролета L =150 мм, момент инерции I = 213333,33мм4, kF = 0,33 мм-1).
Тогда
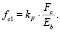(14)
Таким образом, математическая модель описания диаграммы деформирования материала при изгибе с использованием одного параметра (Fc), с учетом (12) и (14), будет иметь вид
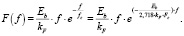(15)
В качестве примера (таблица, точка «1») определяем опытный начальный модуль упругости: Eb = kF*0,6Fc/f1 = 0,33*2100/0,02 = = 3,465*104 МПа.
Как показали опыты (таблица), на нисходящей ветви диаграммы происходит динамическое движение магистральной трещины, что сказывается на характере деформирования реального образца из мелкозернистого шлакобетона.
На основании экспериментальных данных предложена зависимость для коэффициента kf , показывающего величину снижения действующей внешней нагрузки из-за динамического разрушения сечения элемента в нижней растянутой зоне на нисходящей ветви, начиная с величины прогиба f = fc
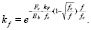(16)
Тогда, с учетом (16) математическая модель описания диаграммы деформирования материала при неупругом изгибе (15), будет иметь вид:
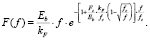(17)
С использованием формулы (17) и с учё- том экспериментальных значений на рис. 3 построена полная равновесная диаграм- ма «F – f».
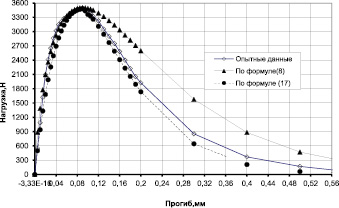
Рис. 3. Диаграмма деформирования «F-f», построенная по формулам (8) и (17), в сравнении с экспериментальными значениями
Математическое прогнозирование разрушения материала.
Считаем, что материал разрушается и теряет свою работоспособность в точке перегиба нисходящей линии диаграммы (при F = Fcc и f = fcc), то есть, когда вторая производная равна нулю:
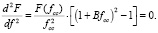(18)
Отсюда находим, что точка перегиба диаграммы разрушения бетона
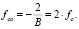(19)
Следовательно, можно считать, что ресурс материала исчерпан при
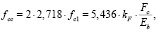(20)
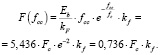(21)
В нашем случае в приведённом примере на основании формул (20) и (21) получаем, что fcc ≈ 0,181 мм, а Fcc ≈ 2090 Н (точка «3»). Как видим, точку «3» можно принять за момент потери ресурса материала.
Важным фактором является то, что эта точка определяется через начальный параметр полной диаграммы деформирования материала в упругой зоне деформации.
Таким образом, предложенная математическая модель описания полной равновесной диаграммы деформирования (ПРДД) с использованием только одного опытного параметра (наибольшей нагрузки Fс) и известного начального модуля упругости материала позволяет исключить проведение сложных равновесных опытов, связанных с постоянной регистрацией прогибов на каждой ступени нагружения, и способна моделировать работу материала на любой стадии нагружения, вплоть до разрушения.