Процесс обработки почвы орудием является чрезвычайно сложным с точки зрения физики, геометрии и математического анализа. Для адекватного представления в модели процесса обработки почвы необходимо учитывать геометрическую конфигурацию орудия и структурно-механические свойства почвы. Поэтому математическая модель должна обладать высоким пространственным разрешением для корректного воспроизведения почвы и формы рабочих органов, а также достаточным временным разрешением, чтобы адекватно описывать перемещение почвы под воздействием рабочих органов орудия. На данный момент существует несколько различных методов математического моделирования процесса взаимодействия почвы с рабочими органами почвообрабатывающих машин.
Классическая почвенная механика рассматривает большинство рабочих органов почвообрабатывающих орудий как разновидности двугранного или трехгранного клина. Поэтому предполагается что, исследовав характер деформаций почвы при воздействии на них клина, можно перейти к изучению деформаций почвы, возникающих при работе почвообрабатывающих и землеройных орудий [1]. Наиболее распространенной схемой взаимодействия клина с почвой в настоящее время является схема процесса деформации пласта клином, предложенная Горячкиным, Пановым и Синеоковым [2, 3].
Другой подход, получивший интенсивное развитие в связи с ростом вычислительных возможностей компьютерной техники и развитием САПР, заключается в применении методов численного моделирования. Здесь можно выделить два типа методов – континуальные и дискретные. К континуальным методам относится метод конечных элементов (FEM – finite element method) заключающийся в разбиении на конечное количество подобластей (элементов) области, в которой ищется решение дифференциальных уравнений. Данный метод нашел достаточно широкое применение в исследованиях процессов обработки почвы [4–6]. Анализ исследований показывает, что достоверность сил, полученных этим методом, даже при использовании нелинейных моделей почвы недостаточна. Движение почвенных агрегатов воспроизводится либо недостоверно, либо весьма грубо.
Также к континуальным методам относится вычислительная гидродинамика (CFD – computational fluid dynamics). Это подраздел механики сплошных сред, включающий совокупность физических, математических и численных методов, предназначенных для вычисления характеристик потоковых процессов. Данный метод нашёл значительно меньшее распространение при исследовании почвенных взаимодействий из-за значительных погрешностей получаемых сил и отсутствия возможности оценки движения почвенных агрегатов [7–9].
Таким образом, использование континуальных численных методов не всегда дает достоверный результат, из-за предположения о непрерывности почвенной среды.
Наиболее эффективно преодолевает недостатки непрерывных численных методов метод дискретных элементов (DEM – discrete element method). Он позволяет описывать разрушение почвы, деформацию и смещение почвенных агрегатов, а также получать различные силовые характеристики [10–12].
Схожими возможностями с методом дискретных элементов обладает метод динамики частиц. Он состоит в представлении среды в виде совокупности взаимодействующих частиц – материальных точек или твердых тел.
Проведенный анализ методов моделирования показал, что наиболее перспективным является метод дискретных элементов (DEM) и родственный с ним метод динамики частиц. Они позволяют достоверно оценить как силовые, так и качественные характеристики процесса обработки почвы.
Цель исследования: имитационное моделирование процесса взаимодействия батарейного дискового рабочего органа с почвенной средой методом дискретных элементов.
Материалы и методы исследования
Опишем принципы механического движения элементов почвы дискретной модели, использованной в исследовании.
При контакте элементов почвы друг с другом и с рабочими поверхностями орудия возникают упругие силы FY, а также силы сухого FС и вязкого трения FВ (рис. 1).
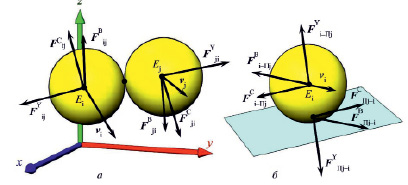
Рис. 1. Схемы силового контакта элементов почвы: а) силы, возникающие при контакте двух элементов почвы; б) силы, возникающие при контакте элемента почвы и поверхности рабочего органа

Рис. 2. Модель рабочего органа: а) исходная модель; б) упрощенная модель; в) расчетная модель
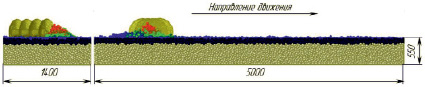
Рис. 3. Виртуальный почвенный канал, использованный при моделировании
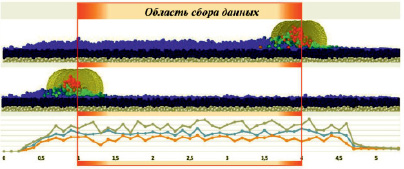
Рис. 4. Область сбора данных
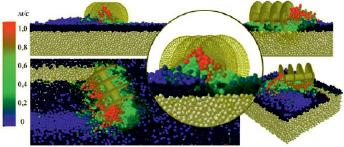
Рис. 5. Процесс моделирования
Движение элементов почвы под действием указанных сил рассчитывается по законам классической динамики. При моделировании воспроизводится изменение состояния системы элементов почвы (процесс обработки почвы) и определяется суммарное механическое воздействие элементов на движущиеся рабочие органы орудия, что позволяет рассчитать потребляемую мощность.
Моделирование производится в трехмерном декартовом пространстве (x, y, z). Состояние каждого элемента Ei задается шестью переменными: координатами его центра (xi, yi, zi) и компонентами скорости (vxi, vyi, vzi).
Для проведения имитационных исследований была создана детализированная 3D-модель дискового батарейного рабочего органа в среде САПР SolidWorks (рис. 2, а). С целью оптимизации процесса моделирования геометрия модели была упрощена (рис. 2, б). Далее упрощенная модель экспортировалась из САПР в формат STL (модель представляется совокупностью треугольных граней, которые описывают поверхность, и нормали) (рис. 2, в).
Использованный в исследовании виртуальный почвенный канал имеет длину 5 м и ширину 1,4 м (рис. 3).
Участок почвенного канала, на котором осуществлялся сбор данных, был выбран длиной в 3 м и расположен в центральной части канала (рис. 4). Именно в этой области, по результатам предварительных экспериментов, наблюдался установившийся режим. Скорость рабочего органа принималась равной 1 м/с, а общее время моделирования 5 с. Соответственно, интервал сбора данных был 1…4 с.
Радиус почвенных частиц во всех сериях экспериментов составлял 18 мм, при этом использовалась исключительно сферическая форма. Плотность почвенных частиц принималась равной плотности твердой фазы почвы 2500 кг/м3. При засыпке почвенных частиц образовавшийся почвенный пласт обладал значительно меньшей плотностью порядка 1600 кг/м3, что соответствует плотности естественных лесных почв.
Для визуального контроля результатов моделирования и оценки смещения почвенных частиц использовались цветовые эпюры скоростей движения частиц (рис. 5).
Контроль силовых параметров процесса производился по трем составляющим вектора тягового сопротивления: проекция силы на ось Х (FX – продольная составляющая), проекция силы на ось Y (FY – боковая сила) и проекция силы на ось Z (FZ – вертикальная составляющая), а также по потребляемой мощности (N) (рис. 6).
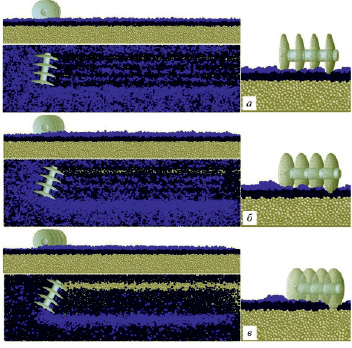
Рис. 6. Моделирование рабочего процесса дискового культиваторного рабочего органа: а) угол атаки α = 10°; б) α = 20°; в) α = 30°
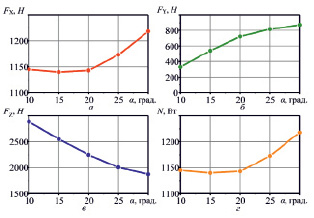
Рис. 7. Влияние угла атаки дисковой батареи α на силовые характеристики, испытываемые рабочим органом: силу тяги FX (а), силу бокового увода FY (б), выглубляющую силу FZ (в), тяговую мощность N (г)
Результаты исследования и их обсуждение
Для демонстрации возможностей использованного метода приводятся результаты моделирования рабочего процесса дискового батарейного рабочего органа, при постоянной глубине обработки 10 см, углах атаки 10, 15, 20, 25 и 30 °.
На рис. 6 представлен почвенный канал после проведения виртуального эксперимента по взаимодействию дискового батарейного рабочего органа с почвенной средой (а – угол атаки α = 10 °; б – α = 20 °; в – α = 30 °). Визуализация процесса почвообработки позволяет как оценить некоторые технологические параметры процесса, так и осуществлять контроль моделирования, выявляя грубые ошибки.
Также виртуальный эксперимент позволяет исследовать силовые нагрузки, испытываемые рабочим органом. Так при углах атаки 10...20 ° сила тяги FX и, соответственно, потребляемая мощность N малы и практически не зависят от α (рис. 7). Однако при увеличении угла атаки α более 20 ° сила тяги и потребляемая мощность существенно возрастают. Это объясняется переходом дисковой батареи в режим хорошей заглубляемости и интенсивной фрагментации почвы. С увеличением угла атаки возрастает также и сила бокового увода батареи FY, что требует принятия компенсационных мер, а в случае двух противоположно ориентированных дисковых батарей – согласованного заглубления батарей для исключения бокового смещения. В то же время выталкивающая сила FZ снижается с увеличением α из-за улучшения заглубления дисковой батареи.
Таким образом, увеличение угла атаки дисковой батареи приводит к росту силы тяги, потребляемой мощности и повышает требования к фиксации батареи от бокового увода, однако приводит к уменьшению выталкивающей силы.
Заключение
Проведенные исследования показали, что метод конечных элементов FEM может применяться для моделирования связных почв, позволяя получать как силовые характеристики, так и данные о процессе разрушения и смещения почвенного массива. Метод вычислительной гидродинамики CFD может эффективно применяться только для исследования силовых характеристик переувлажненных почв. Попытки распространить данный подход на более широкий спектр почв ведут к возникновению значительных ошибок. Наибольшей универсальностью и достоверностью данных обладают дискретные методы. Так дискретный метод динамики частиц позволяет достоверно оценить как силовые, так и качественные характеристики процесса обработки почвы. Например, форму поперечного профиля, степень разрыхления (уплотнения) почвы, характер перемешивания почвенных слоев. При этом могут исследоваться рабочие органы сложной геометрической формы и рабочие органы с активным приводом.



