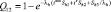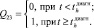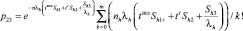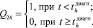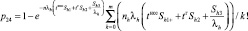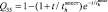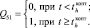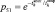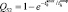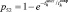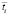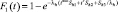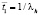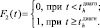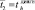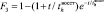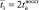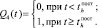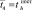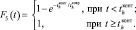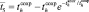Scientific journal

Modern high technologies

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

Для того чтобы гарантировать требуемую надежность технологического оборудования (ТлОб) ракетно-космических комплексов (РКК), придается система обеспечения запасными частями (ЗЧ), которая включает средства для проведения диагностических и ремонтных работ, запасные части и т.д.

Основу комплекта запасных частей и принадлежностей составляют ЗЧ, а их запас определяется начальным количеством, общими затратами и периодичностью пополнения. Под отказом запаса будем понимать событие, заключающееся в том, что заявка на ЗЧ не удовлетворяется в ЗИП, по причине того, что на момент её поступления требуемая номенклатура в ЗИП отсутствует.

В соответствии с [1] под стратегией пополнения запаса понимается ряд правил, на основании которых пополняют запас в комплекте ЗИП. Этими правилами определяются временные границы, длительность и источник пополнения.

В соответствии с [1] предлагаются следующие стратегии пополнения запасов:

- периодическое;

- периодическое пополнение с экстренными доставками;

- непрерывное;

- пополнение по уровню неснижаемого запаса.

Однако в научной литературе [2–4] предлагается использовать ещё две стратегии пополнения, это поставка ЗЧ на весь назначенный срок службы и поставка ЗЧ при возникновении отказа от производителя. Применение данных стратегий пополнения обусловлено в первом случае огромными затратами на лишние ЗЧ и их эксплуатацию (хранение, ТО, ремонт), но довольно высокой готовностью оборудования; для второго – низкая готовность оборудования, высокие затраты на транспортирование ЗЧ и на поддержание в рабочем состоянии оборудования, его производящего, но исключение затрат на «лишние» ЗЧ.

Таким образом, в предлагаемой модели будут рассматриваться следующие стратегии пополнения:

- поставка ЗЧ на весь назначенный срок службы;

- периодическое пополнение с периодом 1 год;

- поставка ЗЧ при возникновении отказа от производителя.

Цель исследования: разработка модели готовности системы обеспечения запасными частями технологического оборудования ракетно-космического комплекса, позволяющей сформировать оптимальное сочетание объема и стратегий пополнения комплектов ЗЧ ТлОб РКК, обеспечивающих требуемое значение коэффициента готовности оборудования с учётом минимальных затрат.

Модель готовности системы обеспечения ЗЧ ТлОб РКК

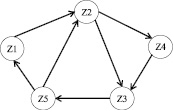
Элемент может одновременно находиться лишь в одном состоянии i = 1,…,n из всего множества (рисунок). В момент времени t = 0 элемент находится в одном из состояний 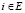и проводит в нем случайное время τ1. В момент времени t = τ1 элемент мгновенно перемещается в новое состояние 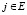с вероятностью 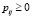, причем 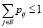для любого 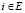. В состоянии j элемент пребывает случайное время τ2, распределенное по закону с произвольной функцией распределения и затем переходит в очередное состояние и т.д.

Для получения характеризующих модель зависимостей использован подход, приведенный в [4]. Опустим выводы и вычисления и приведем итоговые выражения, описывающие состояния графовой модели (табл. 1).

Вероятность нахождения в работоспособном состоянии Z1 является, по сути, коэффициентом готовности, по которому можно судить о её функционировании, причем

Кг = 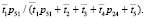(1)

Для определения зависимости коэффициента готовности h-й номенклатуры от количества ЗЧ и стратегий их пополнения подставим в выражение (1) вышеприведенные вероятностные и временные характеристики модели и получим следующую зависимость

(2)

где λh – интенсивность отказов ЗЧ h-й номенклатуры;

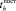– математическое ожидание времени поставки ЗЧ h-й номенклатуры;

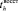– математическое ожидание времени восстановления ЗЧ h-й номенклатуры;

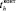– математическое ожидание времени контроля оборудования после замены ЗЧ h-й номенклатуры;

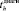– математическое ожидание длительности выявления причины выхода из строя оборудования, связанного с отказом ЗЧ h-й номенклатуры;

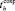– математическое ожидание времени сохраняемости ЗЧ h-й номенклатуры, находящейся в комплекте ЗЧ;

mh – количество ЗЧ h-й номенклатуры;

S – множество стратегий пополнения ЗЧ;

nh – количество однотипных элементов h-й номенклатуры в оборудовании;

tг – период, равный одному году;

tнсс – назначенный срок службы системы.

Модель затрат на обеспечение ЗЧ при различных стратегиях пополнения

Выбор стратегии пополнения определяется многими факторами:

– наличием производства запасов и их доступностью;

– расстояниями от производителей до потребителя;

– стоимостью доставки запасов;

– наличием складов;

– возможностями организации хранения;

– мобильностью потребителя и др.

Однако для проведения обоснованного выбора стратегии пополнения необходимо построить стоимостную модель, позволяющую получить величину затрат на обеспечение ЗЧ, учитывающую не только требуемое количество ЗЧ, но и различные стратегии пополнения. К затратам на обеспечение ЗЧ будем относить затраты на закупку ЗЧ, их поставку, хранение и обслуживание.

При выборе множества стратегий пополнения необходимо учесть особенности эксплуатации ТлОб РКК и требования эксплуатационной документации на оборудование.

В данной модели учтены следующие стратегии пополнения:

– пополнение ЗЧ на весь назначенный срок службы;

– ежегодное пополнение ЗЧ;

– пополнение ЗЧ с периодом её средней наработки на отказ.

Учитывая описанное выше, модель затрат на обеспечение ЗЧ при различных стратегиях пополнения будет иметь следующий вид

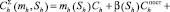
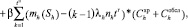(3)

где Sh1 – поставка ЗЧ h-й номенклатуры на период назначенного срока службы (tn = tнсс);

Sh2 – периодическое пополнение ЗЧ h-й номенклатуры (tn = tг);

Sh3 – периодическое пополнение ЗЧ h-й номенклатуры (tn = 1/λh);

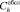– годовые затраты на обслуживание одной ЗЧ h-й номенклатуры;

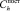– стоимость одной поставки ЗЧ h-й номенклатуры;

Сh – стоимость покупки одной ЗЧ h-й номен- клатуры;

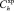– годовые затраты на хранение одной ЗЧ h-й номенклатуры;

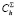– суммарные затраты на обеспечение ЗЧ h-й номенклатуры;

tп – период пополнения ЗЧ;

– количество поставок ЗЧ.

Определение оптимального состава комплекта ЗЧ ТлОб РКК и стратегий его пополнения

Для синтеза объема и стратегий пополнения комплекта ЗЧ оборудования, состоящего из множества запасных частей, воспользуемся алгоритмом, который позволит сформировать количественный состав ЗЧ и оптимальные стратегии его пополнения, обеспечивающие коэффициент готовности изделия не ниже заданного, а объем затрат минимальным [5]. Основу алгоритма составляет метод динамического программирования.

Пример применения моделей

Рассмотрим применение моделей для формирования оптимального комплекта ЗЧ и стратегий его пополнения автоматизированной системы управления техническим комплексом, позволяющих обеспечить коэффициент готовности системы не ниже 0,97 в течение назначенного срока эксплуатации (13 лет).

Пусть поток отказов простейший, параметр потока отказов примем равным интенсивности отказов, параметры потока примем и как величины обратно пропорциональные математическим ожиданиям длительностей соответствующих процессов.

В нашем случае отказ любого элемента системы приводит к отказу всей системы. Исходя из этого, коэффициент готовности системы будем определять как произведение частных коэффициентов готовности входящих в неё составных элементов. Значение частного коэффициента готовности системы, без элементов номенклатуры комплекта ЗЧ, составляет 0,9775. Зная требуемое значение коэффициента готовности системы и значение его частного коэффициента готовности, получим требуемое значение коэффициента готовности системы обеспечения ЗЧ, равное 0,9923.

Для получения оптимального количественного состава ЗЧ и стратегий его пополнения воспользуемся алгоритмом определения количественного состава комплекта ЗЧ и стратегий его пополнения. Использование алгоритма позволило сформировать состав ЗЧ и стратегии его пополнения для номенклатуры комплекта ЗЧ (табл. 2).

Таблица 2

Состав и стратегии пополнения ЗЧ

Стоимость обеспечения ЗЧ составит 7018 ден. ед.

Результаты исследования и их обсуждение

Результатом данного исследования является разработка Модели готовности системы обеспечения ЗЧ и Модели затрат на обеспечение ЗЧ при различных стратегиях пополнения, позволяющих снизить затраты на обеспечение ЗЧ при выполнении требований к коэффициенту готовности системы. Полученные результаты обсуждалась в ходе двух конференций.

Заключение

Описанная в статье модель готовности системы обеспечения ЗЧ ТлОб РКК построена на основе полумарковского подхода, что позволяет ей быть достаточно гибкой и учесть особенности эксплуатации ТлОб РКК. Она отличается от известных тем, что в ней кроме экспоненциального закона применены законы Эрланга и Пуассона. Применение модели позволяет оценить взаимовлияние объема и стратегии пополнения ЗЧ на коэффициент готовности системы.