Система управления выполнением отдельных контрактов по гособоронзаказу (ГОЗ) дочерними предприятиями на уровне промышленного концерна оборонно-промышленного комплекса (ОПК) позволяет повысить их эффективность на основе более широкого выбора стратегий, подходов, интеграции и распределения ресурсов [1]. В связи с формированием системы корпоративного контроля и управления эффективностью выполнения контрактов по ГОЗ необходима организация соответствующего взаимодействия управляющей компании и дочерних предприятий. Выделение этапов выполнения производственных программ позволяет получить контрольные точки оценки эффективности выполнения ГОЗ на этапах производства продукции [1]. Необходима разработка методов и механизмов оценки эффективности поэтапного выполнения каждого контракта ГОЗ и обеспечения поддержки принятия управляющих решений.
Цель исследования: развитие методов и моделей обработки информации и поддержки принятия решений относительно эффективности выполнения ГОЗ при взаимодействии управляющей компании с дочерними предприятиями в структуре концерна.
Методы обработки информации в системе корпоративного управления эффективностью выполнения гособоронзаказа
Мониторинг эффективности выполнения контрактов по ГОЗ дочерними предприятиями Концерна со стороны управляющей компании ведется на основе системы показателей [2]. Основа эффективной работы на предприятиях ОПК – обеспечение постоянного контроля отклонений [3]. Для каждого этапа выполнения отдельного контракта формируется свой перечень показателей. В структуре концерна дочерние предприятия могут выполнять разные, не связанные между собой контракты по ГОЗ, выпускать различную номенклатуру продукции. При этом качественные и количественные показатели эффективности выполнения ГОЗ в каждом конкретном случае могут отличаться.
Механизмы формирования и управления потоками информации представляют собой ряд организационных мероприятий, включающих сбор, обработку, систематизацию информации, определение ее достоверности. Возникает достаточно большой объем собранной информации по показателям, которые, с одной стороны, дополняют друг друга, с другой стороны, требуют согласования между собой. Эта информация является избыточной и сложной для анализа на верхнем уровне менеджмента.
На уровне корпоративного менеджмента выделяются задачи: проверки достоверности собранной информации, а также обобщения и анализа собранной информации. Степень обобщения и уровень детализации анализа при обработке информации должны обеспечить выделение существенных для планируемых результатов явлений и процессов, исключая при этом «зашумленность» незначимыми отклонениями и возмущениями. Вторая задача требует группировки частных показателей, наиболее значимых для того или иного фактора риска выполнения производственной программы.
Для обработки информации и поддержки принятия решений могут быть применены известные методы анализа данных [4]. Среди них методы: статистической обработки информации; нечеткой логики; «мозгового штурма»; теории графов и др. Реализации частных показателей в общем случае носят случайный характер. В этом случае оценку, а также принятие решений удобно осуществлять с применением экспертного подхода. Для сокращения числа экспертных оценок по проектам целесообразным представляется подход, основанный на факторном анализе групп показателей (анализ факторов риска) [5].
Для организационных систем сохраняется вероятностный характер влияния промежуточных показателей на результат выполнения работы, проявляется сложная взаимосвязь различных факторов риска. Поскольку исходная информация для принятия решения об эффективности выполнения контракта по ГОЗ носит нечеткий характер, то само решение также является нечетким. В этой связи в рамках данной работы предложено использовать аппарат нечеткой логики [6].
Модель оценки достоверности информации об эффективности выполнения гособоронзаказа в структуре концерна
Каждый фактор риска на этапах производства вооружений и военной техники характеризуется соответствующей группой показателей (трудовые ресурсы, производственные фонды, финансы, качество продукции, сроки). Эксперты в соответствии с их специализацией для каждого реализуемого проекта оценивают показатели – каждый в своей области, на предмет соответствия установленным нормам. Выявленные экспертами малые или критические отклонения от нормативных значений показателей характеризуют факторы риска выполнения контрактов ГОЗ. Такой подход позволяет осуществлять независимую или перекрестную экспертизу проектов. Появляется возможность оценить согласованность экспертных мнений, взаимосвязь оценок по группам факторов риска.
Оценку достоверности рационально осуществить путем сопоставления экспертных оценок по факторам риска с учетом их взаимосвязи: при появлении отклонений в одной группе показателей следует ожидать отклонений в других. Для построения нечеткой модели в виде базы нечетких правил вывода введем входные лингвистические переменные, соответствующие экспертным оценкам по группам показателей:
X1 = «Эффективность использования трудовых ресурсов по показателям» c универсальным множеством U(X1) = [0, 1]. Терм-множество T(X1) = {«норма», «отклонения», «критические отклонения»}.
X2 = «Эффективность использования производственных фондов «по показателям)» с универсальным множеством U(X2) = [0, 1]. Терм-множество T(X2) = {«норма», «отклонения», «критические отклонения»}.
X3 = «Эффективность использования финансовых средств» с универсальным множеством U(X3) = [0, 1]. Терм-множество T(X3) = {«норма», «отклонения», «критические отклонения»}.
X4 = «Качество выполнения заказа» с универсальным множеством U(X4) = [0, 1]. Терм-множество T(X4) = {«норма», «отклонения», «критические отклонения»}.
X5 = «Оценка динамики производства». Универсальное множество переменной X5 содержит два значения: 0 и 1. Терм-множество T(X5) = {«норма», «отклонения», «критические отклонения»}.
Выход нечеткой модели формализуется лингвистической переменной Y = «Оценка достоверности информации», c универсальным множеством U(Y) = [0, 1]. Терм-множество T(Y) = {«достоверна», «не достоверна»}.
Для терм-множеств каждой лингвистической переменной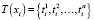 
экспертами определяются функции принадлежности 
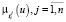(рис. 1) с характерными точками, имеющими следующий смысл: u1 – минимальное значение переменной на множестве U(Xi), которое не принадлежит значению лингвистической переменной; u2 – минимальное значение переменной, которое точно принадлежит значению лингвистической переменной; u3 – максимальное значение переменной, которое точно принадлежит значению лингвистической переменной; u4 – максимальное значение переменной, которое не принадлежит значению лингвистической переменной.
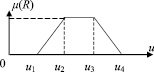
Рис. 1. Описание функций принадлежности лингвистических переменных
Пример функций принадлежности для терм-множеств входных и выходной лингвистических переменных приведен на рис. 2.
Рис. 2. Функции принадлежности входных и выходной лингвистических переменных нечеткой модели проверки достоверности информации
Система нечетко-продукционных правил нечеткой модели сформирована на основе обобщения опыта работы экспертного сообщества и включает 153 правила. Приведем некоторые из них:
1. Если T(X1) = критические отклонения, И T(X3) = критические отклонения, И T(X4) = критические отклонения ТО T(Y) = достоверно.
2. Если T(X1) = норма, И T(X2) = норма, И T(X3) = критические отклонения ТО T(Y) = не достоверно.
3. Если T(X1) = отклонения, И T(X2) = отклонения И T(X3) = критические отклонения, И T(X4) = критические отклонения ТО T(Y) = не достоверно.
…
153. Если T(X1) = критические отклонения, И T(X2) = критические отклонения И T(X3) = критические отклонения, И T(X4) = отклонения, И T(X5) = критические отклонения ТО T(Y) = достоверно.
Агрегирование нечетких правил и аккумуляцию решения в системе нечеткого вывода осуществим по алгоритму Мамдани [6, 7]. Дефаззификация в системе нечеткого вывода позволяет перейти от функций принадлежности выходной лингвистической переменной к четкому, числовому значению оценки достоверности информации. Приведение к четкости проводится центроидным методом:
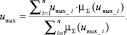(1)
Рассмотрим пример применения модели оценки достоверности информации об эффективности выполнения ГОЗ по экспертным оценкам. Пусть по собранному множеству показателей о ходе выполнения ГОЗ, для трех анализируемых контрактов К1, К2, К3, в соответствии с разработанной методологией определены экспертные оценки (табл. 1).
Таблица 1
Значения входных переменных на множестве U(Xi)
|
Контракт |
U(X1) |
U(X2) |
U(X3) |
U(X4) |
U(X5) |
|
К1 |
0,9 |
0,8 |
1,0 |
0,9 |
0,9 |
|
К2 |
0,4 |
0,4 |
0,5 |
0,6 |
0,5 |
|
К3 |
0,5 |
0,7 |
0,9 |
0,9 |
0,8 |
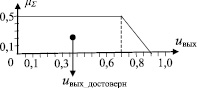
С учетом принятых интервалов значений входных и выходной лингвистических переменных (рис. 2) осуществляется процедура нечеткого вывода для каждого контракта по известным методикам [6]. Вывод функции принадлежности выходной переменной по алгоритму Мамдани позволяет получить точки ее перегиба (рис. 3): μΣ (0,5) = 0; μΣ (0,7) = 0,5; μΣ (1) = 0,5; μΣ (1) = 0. Оценка достоверности информации в соответствии с (1):
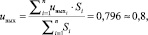(2)
где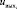 
– центр тяжести фигуры, выделенной под частью функции принадлежности, а Si – площадь этой фигуры (рис. 3).
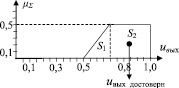
Рис. 3. Дефаззификация выходной переменной для первого контракта по методу Мамдани
Аналогично для второго и третьего контрактов процедура нечеткого вывода позволяет получить вид функции принадлежности нечеткого вывода, представленный на рис. 4, а, и рис. 4, б, соответственно. Результаты расчетов для трех вариантов сведены в табл. 2.
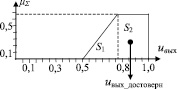
а) б)
Рис. 4. Дефаззификация выходной переменной по методу Мамдани для: а) Контракта К2; б) Контракта К3
Таблица 2
Результаты оценки достоверности информации об эффективности выполнения ГОЗ по примерам для трех контрактов
|
Контракт |
Численная оценка показателя |
Лингвистическая оценка достоверности информации |
|
К1 |
0,796 |
Достоверно (высокая достоверность) |
|
К2 |
0,8088 |
Достоверно (высокая достоверность) |
|
К3 |
0,4021 |
Не достоверно |
Численные значения выходной переменной являются более дифференцированными по сравнению с лингвистической выходной переменной. Сопоставление показателей достоверности информации позволяет ранжировать список контрактов по точности экспертных оценок и исключить принятие решений по заведомо недостоверной информации.
Представленная оценка достоверности информации может использоваться также для проверки согласованности экспертных мнений. При этом полагается: что все эксперты не могут ошибаться одновременно и в равной степени. Тогда результат не достоверности информации свидетельствует о необходимости дополнительной, более тщательной экспертизы сведений, с возможным привлечением другого состава экспертов.
Модель оценки риска выполнения гособоронзаказа дочерними предприятиями концерна
Экспертные оценки собранных множеств показателей позволяют оценить риски выполнения ГОЗ дочерними предприятиями в структуре концерна. Дифференциальная оценка показателя риска позволит выявить наиболее уязвимые этапы производства по контрактам и учитывать их при распределении ресурсов внутри концерна.
Для построения нечеткой модели в виде базы нечетких правил вывода используются входные лингвистические переменные предыдущей модели. Выход нечеткой модели формализуется лингвистической переменной Y = «Риск выполнения контракта», c универсальным множеством U(Y) = [0, 1]. Терм-множество T(Y) = {«отсутствует», «низкий», «средний», «критический»}.
Вид функций принадлежности для терм-множеств входных и выходной лингвистических переменных приведен на рис. 5. Система нечетко-продукционных правил модели сформирована на основе обобщения опыта работы экспертного сообщества и включает 69 правил нечеткой модели. Приведем некоторые из них:
1. Если T(X3) = критические отклонения, ТО T(Y) = критический.
2. Если T(X4) = критические отклонения, ТО T(Y) = критический.
3. Если T(X5) = критические отклонения, И Если T(X4) = отклонения, ТО T(Y) = критический.
4. Если T(X1) = критические отклонения, И T(X2) = критические отклонения, ТО T(Y) = критический.
…
69. Если T(X1) = норма, И T(X2) = норма, И T(X3) = норма, И T(X4) = норма, И T(X5) = норма, ТО T(Y) = отсутствует.
Рис. 5. Функции принадлежности входных и выходной лингвистических переменных нечеткой модели оценки риска выполнения контракта по ГОЗ. Обозначения на графике μY(u): 0 – риск отсутствует; 1 – риск низкий; 2 – риск средний
Агрегирование нечетких правил и аккумуляция решения в системе нечеткого вывода осуществляется по алгоритму Мамдани [6, 7]. Дефаззификация в системе нечеткого вывода позволяет перейти от функций принадлежности выходной лингвистической переменной к четкому, числовому значению оценки риска выполнения контракта по ГОЗ. Приведение к четкости проводится аналогично (1).
В ходе разработки приведенных выше нечетких моделей проведено их обучение, настройка. Полнота представленных математических моделей обеспечивается за счет перебора достаточного количества обучающих выборок при их проектировании.
Заключение
Проведенный анализ подходов к решению задач проверки достоверности собранной информации, а также ее обобщения с целью обеспечения управляющих решений показал, что анализ удобно осуществлять с применением экспертного подхода. На основе методов теории нечетких множеств разработана модель оценки достоверности информации о ходе выполнения контрактов по ГОЗ дочерними предприятиями концерна, а также модель оценки риска выполнения контрактов по ГОЗ дочерними предприятиями концерна. Численные оценки выходного показателя моделей являются более дифференцированными по сравнению с лингвистической выходной переменной. Сопоставление численных оценок выходного показателя риска позволяет ранжировать список контрактов по опасности срыва их выполнения и обеспечить принятие решений по наиболее опасным ситуациям. Разработанные модели могут использоваться для любого числа контрактов и предприятий.
Практическая значимость предложенного подхода и разработанных математических моделей состоит в том, что их легко алгоритмизировать и реализовать в составе автоматизированных систем организационного управления.