В настоящее время микромеханические сенсоры широко используются в различной аппаратуре гражданского и военного назначения. Требования к параметрам и показателям микромеханических гироскопов (ММГ) регулярно увеличиваются, так как появляются новые области их использования, которые отличаются высоким уровнем различных внешних дестабилизирующих факторов, в частности более высокими требованиями к параметрам ударов и вибрации [1–3].
Вибрационная и ударная устойчивости микромеханических датчиков в значительной мере определяются кинематикой движений его сенсора [4–6]. Поэтому в качестве основного метода повышения устойчивости к механическим воздействиям микромеханического гироскопа при проектировании можно назвать правильный выбор его кинематической схемы [7, 8].
Целью работы является исследование чувствительности микромеханического гироскопа с антифазным первичным движением к вибрационным воздействиям [9].
Схема и принцип действия
Принцип действия, рассматриваемого в статье двухкомпонентного микрогироскопа, поясняется рис. 1. Гироскоп применяется для измерения угловых скоростей объекта вокруг осей Х и Z. В гироскопе применяется антифазное первичное движение, для этого с помощью гребенчатой структуры 15 вдоль оси Y происходит возбуждение противофазных первичных гармонических колебаний рамок 1, которые крепятся к основанию 19 с помощью упругих элементов 6.
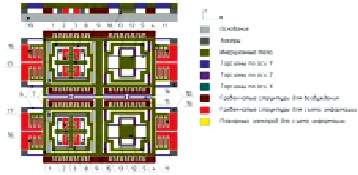
Рис. 1. Схема двухкомпонентного гироскопа с промежуточными телами
Рамки соединены между собой упругим элементом 14, что позволяет им совершать первичные колебания с одной частотой, но в противоположных направлениях. Тела 2 и 4 являются промежуточными и совершают первичные колебания заодно с рамками 1 вдоль оси Y. Это происходит вследствие того, что жёсткость упругих элементов 7 вдоль осей Z, Y намного выше, чем жёсткость этих упругих элементов вдоль оси Х, а жёсткость упругих элементов 13 вдоль осей Y, X намного выше их жёсткости по оси Z.
Инерционные тела 3 соединяются с промежуточными телами 2 упругими элементами 8 и их жёсткость по оси Х намного выше их жёсткости по оси Y. С основанием инерционные тела 3 соединены упругими элементами 9, которые имеют жёсткость по оси Х на несколько порядков меньше, чем по оси Y. Благодаря этому инерционные тела 3 не перемещаются по оси Y при первичных колебаниях.
При появлении угловой скорости Ωz, появляются силы Кориолиса. Данные силы через промежуточные тела 2 и упругие подвесы 8 и 9 возбуждают колебания инерционных тел 3 по оси Х, которые являются информативными. Перемещения инерционных тел 3 преобразовываются в изменения емкостей гребенчатой структуры 17, которые представляют собой преобразователь ёмкость-напряжение (ПЕН).
Инерционные тела 5 также не принимают участия в первичных колебаниях вдоль оси Y. При появлении угловой скорости Ωx, появляются силы Кориолиса, которые направлены по оси Z через промежуточные тела 4 и упругие подвесы 11. Силы Кориолиса возбуждают полезные колебания инерционных тел 5, закреплённых с помощью упругих элементов 12 по оси Z. При перемещениях инерционных тел происходят изменения ёмкостей электродов 18, 19, которые также используются в ПЕН.
Таким образом, используя промежуточные тела, можно изолировать информативные колебания от первичных колебаний. При этом не происходит движения сенсорных гребенчатых структур в направлении первичных колебаний и изменение емкостей сенсорных гребенчатых структур будет зависеть только при их перемещениях вдоль информативных осей.
Математическая модель движения ММГ
Эквивалентные схемы двухкомпонентного микрогироскопа можно представить в виде системы сосредоточенных масс, которые имеют упругое соединение между собой, а также с основанием.
Основание, с которым жёстко связан корпус гироскопа, совершает поступательную синусоидальную вибрацию и поворачивается в пространстве с угловыми скоростями Ωx, Ωу и Ωz. Тогда получим уравнения сенсорных вторичных колебаний вдоль оси Х в виде
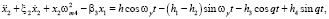
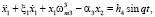(1)
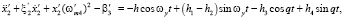
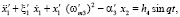
где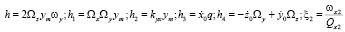 
; 
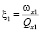; q – частота вибрации; ωy – частота первичных колебаний. Из уравнений видно, что промежуточные рамки и инерционные тела совершают колебания с частотой первичных колебаний и с частотой вибрации по закону
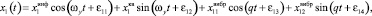
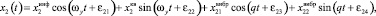(2)
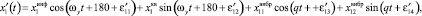
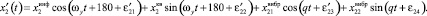
Первые составляющие в формулах (2) представляют собой информативные колебания, амплитуда которых зависит от измеряемых угловых скоростей. Вторые составляющие колебаний, происходящие с частотой первичных колебаний, обусловлены перекрёстной связью между первичным и вторичным каналами. Третьи составляющие колебаний с частотой q зависят от вибрации основания. Информация об измеряемых угловых скоростях и ускорениях объекта содержится в амплитудах колебаний инерционных тел, которые определяются как
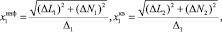
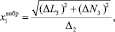
где
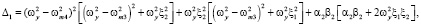
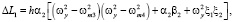
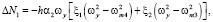(3)
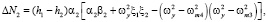
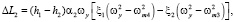
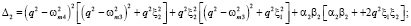
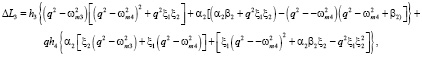
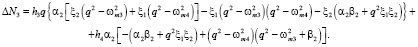
Колебания инерционных тел преобразуются в изменения сенсорных емкостей и затем в выходные сигналы. Колебания инерционных тел по оси Z имеют аналогичный вид, но с параметрами этого канала. Как видно из выражений (2) и (3), на информативные колебания инерционных тел, которые происходят с частотой первичных колебаний, накладываются колебания с частотой вибрации и колебания с частотой первичных колебаний, но сдвинутые на 900 по отношению к информативным колебаниям. Эти колебания представляют собой помеху, которая может быть устранена системой обработки информации. Алгоритм определения угловых скоростей многокомпонентным гироскопом позволяет скомпенсировать вибрационные помехи, так как они имеют противоположные знаки за счёт применения антифазного первичного движения.
Моделирование в среде Matlab Simulink
По результатам моделирования получены следующие результаты. При отсутствии вибрации (рис. 2) промежуточные рамки и инерционные тела совершают колебания с одинаковой амплитудой как единое тело.
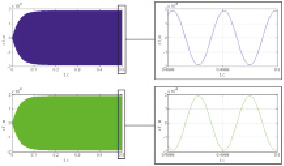
а)
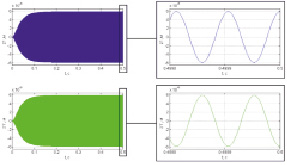
б)
Рис. 2. Колебания ММГ при отсутствии вибрации: а) колебания сенсора гироскопа по оси Х, б) Колебания сенсора гироскопа по оси Z
Вибрация основания вызывает появление колебаний сенсора с частотой вибрации, которые накладываются на первичные (рис. 3, а) и информативные колебания (рис. 3, б, в).
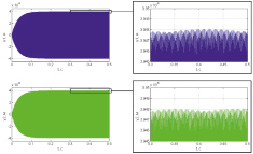
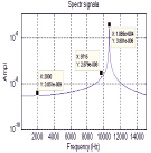
временные характеристики спектр сигнала
а)
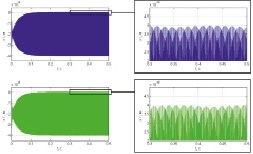
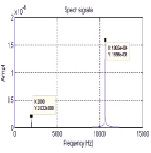
временные характеристики спектр сигнала
б)
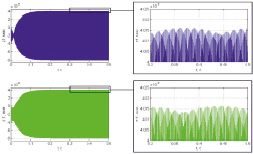
временные характеристики спектр сигнала
в)
Рис. 3. а) первичные колебания гироскопа по оси Y при наличии вибрации, б) колебания сенсора гироскопа по оси Х при наличии вибрации, в) колебания сенсора гироскопа по оси Z при наличии вибрации
Амплитуда первичных колебаний более чем на два порядка превышает амплитуду вибрационных колебаний, следовательно, влиянием вибрации на первичный канал можно пренебречь.
В спектре всех вторичных колебаний имеются две гармоники – основная с частотой возбуждения первичных колебаний и дополнительная с частотой вибрации f = 2 кГц. Амплитуда в спектре на рисунках является не нормированной величиной, а относительной.
Частота информативных колебаний микрогироскопа в пять раз больше максимальной частоты вибрации, следовательно, вибрационную помеху с частотой вибрации можно уменьшить при обработке выходных сигналов. Все собственные частоты гироскопа лежат за пределами диапазона частот вибрации, и резонансного усиления вибрационного воздействия в гироскопе не происходит.
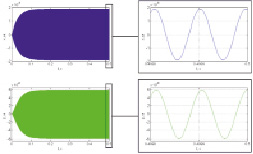
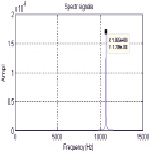
Суммарные колебания (х1 – х1') и (z1 – z1'), по которым определяются угловые скорости (рис. 4), вибрационных колебаний не содержат.
а) б)
Рис. 4. Алгоритм определения угловой скорости при вибрации: а) временные характеристики, б) спектр сигнала
Алгоритм определения угловой скорости идеально компенсирует гармоническую составляющую действующей вибрации (рис. 4), оставляя в спектре выходного сигнала лишь информативную составляющую с частотой первичных колебаний, которая и определяет измеряемую угловую скорость.
Все результаты моделирования получены при условии идентичности параметров информативных каналов. Однако за счёт технологического процесса изготовления различие параметров информативных каналов может достигать 1 %. Кроме того, изменение параметров гироскопа происходит и в результате изменения температуры. Рассмотрим работу алгоритмов определения угловой скорости при различии параметров информативных каналов. Пусть собственные частоты вторичных колебаний различаются на 0,05 %, что составляет 5 Гц.
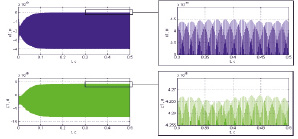
В спектрах вторичных колебаний гироскопа присутствуют: гармоника вибрации и гармоника частоты возбуждения первичного канала (основная частота вторичных колебаний) (рис. 5, а). Алгоритм работает практически так же, как и при совпадении частот вторичных каналов. Составляющие, обусловленные постоянным ускорением, компенсируются. В спектре суммарного сигнала вторичных колебаний гироскопа осталась гармоника вибрационного воздействия, хотя ее амплитуда мала по сравнению с амплитудой информативных колебаний и ей можно пренебречь (рис. 5, б).
а)
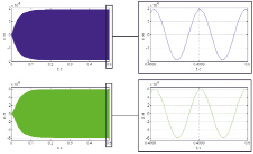
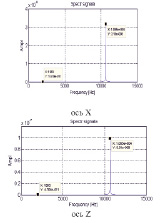
временные характеристики спектр сигнала
б)
Рис. 5. а) колебания гироскопа по информативным осям при различии их собственных частот на 0,05 %, б) алгоритм определения угловой скорости при вибрации
Заключение
Поступательная вибрация основания вызывает колебания гироскопа с частотой вибрации, которые накладываются на информативные колебания. Применение антифазных первичных колебаний гироскопа позволяет уменьшить в выходной информации влияние вибрационных колебаний. Собственные частоты гироскопа превышают частотный диапазон вибрационного воздействия, что исключает возможность возникновения резонансов.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 17-37-50014 «мол_нр».