Экономический кризис последнего десятилетия заставляет более детально исследовать экономико-математические модели, примеры которых представлены в различных источниках [1–4]. Кроме того, очевидно, необходимо уделить особое внимание методам исследования подобных моделей для получения обоснованности получаемых на их основе научных выводов. В связи с вышеизложенным, трудно переоценить актуальность исследования в частности, динамических моделей экономического роста, описывающих подъемы и спады в развитии экономики как модели делового цикла. К числу таких экономико-математических моделей относится исследуемая далее в данной статье модель Самуэльсона – Хикса, связывающая такие макроэкономические показатели, как валовый выпуск, потребление и инвестиции, с параметрами модели – фактором акселерации, склонностью к потреблению и базовым потреблением [5].
Целью исследования в представленной работе является обоснование монотонного роста валового выпуска в зависимости от фактора акселерации для любого фиксированного момента времени и, как следствие, нахождение соответствующего максимального валового выпуска. Предлагаемое далее исследование опирается на строгие математические методы решения линейных разностных уравнений и математического анализа (дифференциальное и интегральное исчисление) [6, 7]. При этом валовый выпуск рассматривается как непрерывная функция меняющегося параметра, а момент времени считается, наоборот, заданным.
Рассмотрим экономику, в которой изменение национального дохода (валового выпуска) происходит под действием следующего принципа акселерации: объемы инвестирования зависят от изменения спроса на конечную продукцию или валового выпуска.
Математическая модель национальной экономики может быть представлена уравнениями
, 
,
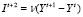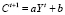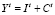
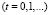, (1)
где It, Yt и Ct – соответственно инвестиции, валовый выпуск и потребление в период t, v > 0 – фактор акселерации, 0 < a < 1 – склонность к потреблению, b > 0 – базовое потребление. Первое из них означает, что инвестиции пропорциональны приросту валового выпуска, второе задает потребление как линейную функцию от выпуска, а третье – условие бюджетного баланса (равенство спроса и предложения). Модель (1), известная в литературе как модель Самуэльсона – Хикса, используется при описании закономерностей, связанных с колебаниями деловой активности [5]. Исключая It и Ct из уравнений (1), получаем уравнение динамики валового выпуска в виде следующего линейного разностного уравнения второго порядка:
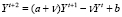
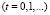, (2)
являющееся линейным неоднородным разностным уравнением второго порядка. Согласно [6], решение уравнения (2) сводится к характеристическому уравнению
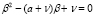
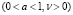(3)
и зависит от знака его дискриминанта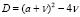 
. В данной работе исследуем оптимизационную задачу: найти значения параметров a и v, при которых валовый выпуск Yt в некоторый момент времени t максимален. Рассмотрим случай, когда D = 0, предполагая базовое потребление b неизменным. Полагаем (не нарушая общности анализа), что выпуски 
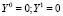. Тогда математическая постановка сформулированной задачи записывается как
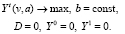(4)
В соответствии с алгоритмом, изложенным в [6], решение уравнения (2) имеет вид
, 
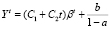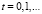, (5)
где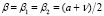 
– единственный корень уравнения (3), а коэффициенты
,
.
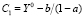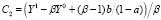В силу нулевых начальных условий,
, 
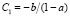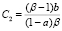. (6)
Поскольку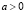 
и 
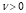, то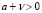 
и условие 
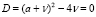равносильно тому, что
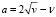. (7)
Так как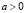 
, то из (7) получим 
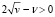или 0 < v < 4. Таким образом, множество содержательных значений параметров a, v описывается линией вида (7), где 0 < v < 4 (рисунок). Так как a < 1, то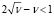 
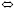
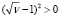или v ≠ 1. Поэтому формально следует исключить значение v = 1, которому, согласно (7), соответствует значение 
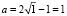, т.е. исключить точку (1;1) кривой, представленной на рис. 1, – точку максимума. Однако для разрешимости задачи параметрической оптимизации (4), в соответствии с теоремой Вейерштрасса о достижении непрерывной функцией на отрезке своей верхней и нижней грани [7], потребуем замкнутости множества значений параметров a, v, включив крайние их значения и указанную точку максимума, т.е. полагаем, что 0 ≤ v ≤ 4 и 0 ≤ a ≤ 1. Очевидно, это множество непусто, а его ограниченность следует из условий 0 < v < 4, 0 < a < 1. В силу формулы (7) корень уравнения (3)
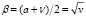
и
,
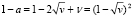поэтому константы (6) преобразуются к виду
,
.
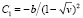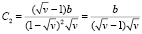При этом выражение (5) для валового выпуска определяется формулой
, 
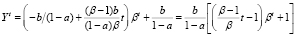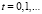, или
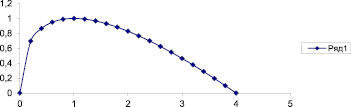
График параметрической зависимости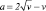 
, 0 ≤ v ≤ 4
, 
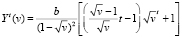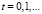
Тогда задача (4) равносильна следующей
, 
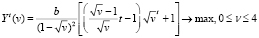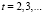(8)
Обозначим
, 
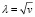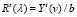. (9)
Так как функция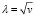 
возрастает по v, от задачи (8) перейдем к эквивалентной задаче
, 
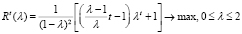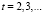или
, 
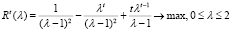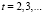(10)
Исследуем на экстремум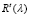 
из (10) как функцию от непрерывного параметра λ:
.
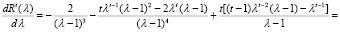
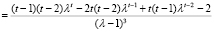Таким образом,
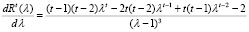. (11)
Обозначая
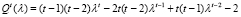, (12)
можем переписать формулу (11) в виде
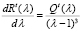. (13)
Дифференцируем (12) по λ:
.
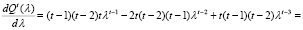
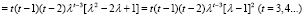Таким образом, получили
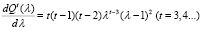, (14)
из которого следует: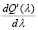 
кратно 
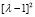. Интегрируя (14) по λ, получим
.
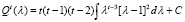Сделаем замену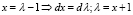 
. Тогда
.
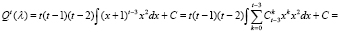
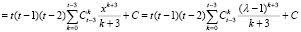В итоге
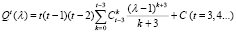, (15)
откуда при λ = 1 имеем Qt(1) = C. С другой стороны, из (12) получим
.
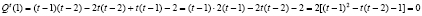Таким образом,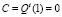 
, поэтому (15) окончательно запишем в виде
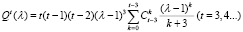. (15’)
Заметим, что из (15’) следует: Qt(λ) кратно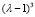 
. Подставляя (15’) в (13), имеем
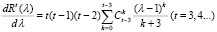. (16)
Кроме того, объединяя выражения (11) и (16), получим тождество
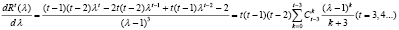, (17)
из которого следует, что λ = 1 – точка устранимого разрыва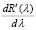 
. Действительно, при 
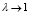из левой части (17) по правилу Лопиталя, с учетом (13) и (14), найдем
.
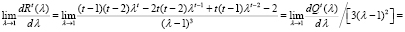
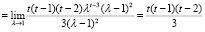С другой стороны, из правой части (17) имеем
,
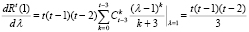т.е.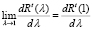 
. Тогда 
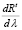доопределим выражением 
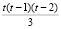, считая ее непрерывной в точке λ = 1, т.е.
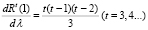. (18)
На основе формулы (16) несложно доказать следующую лемму.
Лемма. Если для уравнения динамики (2) справедливы условия
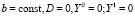, (19)
то
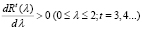. (20)
Доказательство. При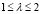 
неравенство (20) очевидно в силу (16), (18) и условий 
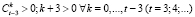. Поэтому достаточно доказать указанное неравенство для 0 ≤ λ < 1. Применяя бином Ньютона к формуле (16), перепишем ее в виде
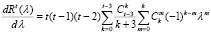. (21)
Рассмотрим двойную сумму более общего вида, чем правая часть (21):
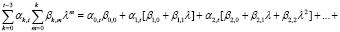
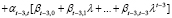
или, упорядочивая слагаемые по степеням λ, имеем
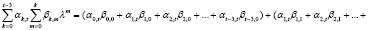
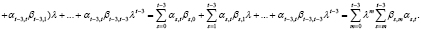
Таким образом, доказано равенство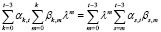 
, в силу которого при 
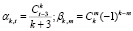, перепишем выражение (21) в виде
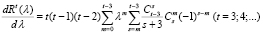. (22)
Рассмотрим внутреннюю сумму по s в правой части (22):
.
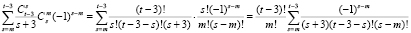Сделаем в последней сумме замену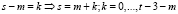 
. Тогда
.
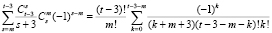Делая в полученной сумме замену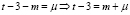 
, запишем
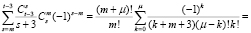
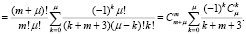
В итоге получим
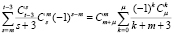. (23)
Рассмотрим тождество, получаемое из бинома Ньютона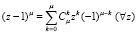 
или
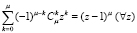. (23’)
Умножая его на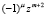 
и учитывая, что 
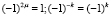, запишем
.
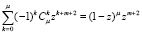
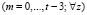Интегрируя полученное тождество по z на интервале от 0 до 1, имеем
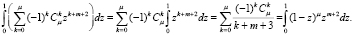
Таким образом,
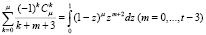. (24)
Так как функция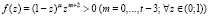 
, то справедлива оценка [7]:
,
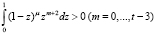из которой, с учетом (24), следует, что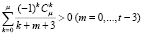 
. Отсюда, в силу (23) и 
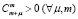, имеем неравенство
,
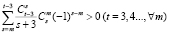означающее, что коэффициенты при λm в выражении (22) положительны. Поэтому справедливо неравенство (20) при λ ≥ 0 и, в частности, при 0 ≤ λ ≤ 2, так как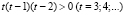 
и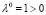 
. При λ = 1 (20) также верно в силу (18).
Из леммы следует, что функция Rt(λ) монотонно возрастает по λ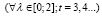 
. Поэтому, в силу соотношений (9), валовый выпуск в момент t также монотонно возрастает по параметру v. Следовательно, наибольшее значение Rt(λ) может достигать лишь на границах отрезка 
:
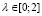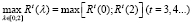. (25)
При t = 2 из (10) имеем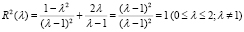 
, т.е. λ = 1 – точка устранимого разрыва. Тогда полагаем
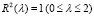. (26)
С другой стороны, по формуле (10) при λ = 0; 2 соответственно найдем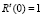 
; 
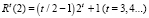, откуда, в силу (26) и неравенства 
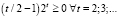, имеем 
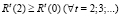, т.е., согласно (25), 
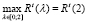. В итоге 
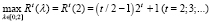. Тогда, с учетом (9), при условиях (19) найдем наибольший валовый выпуск в момент t по формуле
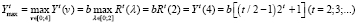. (27)
При этом наибольший валовый выпуск в момент t соответствуют значения параметров v = 4; a = 0.
Таким образом, используя методы решения линейных разностных уравнений, а также дифференциальное и интегральное исчисление, удалось показать, что валовый выпуск в момент t является монотонно возрастающим по параметру фактора акселерации при условиях нулевых валовых выпусков и наличии кратного корня у характеристического уравнения, соответствующего разностному уравнению, описывающему указанный экономический показатель. Это, в свою очередь, позволило получить выражение для максимального валового выпуска в заданный момент времени. Найденное выражение задает оценку сверху на любой валовый выпуск в произвольный момент времени t ≥ 2 в модели роста Самуэльсона – Хикса.