Динамические нагрузки в трансмиссии машин, возникающие в процессе их работы, значительно влияют на надёжность узлов и их элементов. Возникновения колебательных процессов обусловлены как внутренними, так и внешними факторами [1]. К внутреннему фактору можно отнести работу двигателя и жёсткость элементов трансмиссии. В роли внешнего фактора выступают различные силовые воздействия на исполнительных элементах, связанные с условиями работы машины. Например, во время эксплуатации транспортного средства это влияние связано с особенностями рельефа дорожного покрытия и его продольной кривизной.
При работе машин с определённой скоростью возникают резонансные явления в трансмиссии, когда частота вынужденных колебаний совпадает с частотой собственных колебаний механической системы [1–2]. В этом случае значительно возрастают вибрации, воспринимаемые рамой и элементами трансмиссии [3]. Они являются вредным фактором для операторов и других людей, находящихся в непосредственной близости от работающих объектов, и приводят к появлению дополнительных динамических нагрузок в механической системе.
Для поглощения колебаний вблизи резонансных частот механических систем, можно использовать динамический поглотитель колебаний углового типа [4, 5]. Динамический поглотитель представляет массу с моментом инерции Jn, закрепленную на металлоконструкции с помощью упругого элемента с приведенной жесткостью Cn. Величину момента инерции Jn и жесткость пружины Cn выбирают с учетом резонансной частоты трансмиссии ω из соотношения
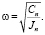
Согласно поставленным задачам методикой экспериментального исследования предусматривалась проверка работоспособности устройства гашения колебаний в трансмиссии машин и получение графиков переходных процессов в колебательной системе. Подтверждением работоспособности поглотителя колебаний будет являться его способность поглощения колебания в заданных режимах работы. При проведении испытаний моделировались условия возникновения резонанса в механической системе и его отсутствие при включении поглотителя колебаний.
Схема экспериментальной установки показана на рис. 1. Основной груз 11, установленн на направляющих 6 и подвешен на пружинах 5. С помощью пружины 15 и троса 7, груз 11 через шарнир 13 кинематически связан с червячным колесом редуктора 8. К редуктору 8 подключён электродвигатель 9 с регулятором напряжения 10, установленный на раме 1. Вращательное движение вала электродвигателя 10 преобразовалось в поступательное движение груза 11. К грузу 11, совершающему поступательное движение в вертикальной плоскости, подвешен на пружине 14 дополнительный груз 12, служащий в качестве поглотителя колебаний. На грузе 11 установлен стержень с пером 4 самописца 3, фиксирующий его колебания на вращающемся барабане, имеющем электропривод 2, установленный на раме 1. На барабане самописца 3 закреплён лист бумаги, на котором осуществлялось фиксирование графиков колебаний груза 11.
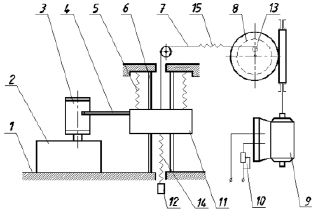
Рис. 1. Схема экспериментальной установки: 1 – рама; 2 – привод барабана самописца; 3 – самописец; 4 – стержень с пером; 5 – пружина; 6 – направляющие; 7 – трос; 8 – редуктор; 9 – электродвигатель; 10 – регулятор напряжения; 11 – груз; 12 – груз поглотителя колебаний; 13 – шарнир; 14, 15 – пружины
Для моделирования явления резонанса увеличивалась частота поступательного движения груза 11. Для этого при помощи регулятора напряжения 10 повышалось напряжение на обмотках электродвигателя 9 и увеличивалась его частота вращения до тех значений, при которых резко увеличивалась амплитуда колебаний груза 11. При проведении экспериментальных исследований фиксировались частота вращения электродвигателя 9 и амплитуды колебаний грузов 11 и 12.
На рис. 2 представлен общий вид экспериментальной установки.
Рис. 2. Общий вид экспериментальной установки
Кинетическая энергия системы равна
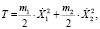
где m1 – масса основного груза;
m2 – масса поглотителя колебаний;
X1 – перемещение основного груза;
X2 – перемещение дополнительного груза.
Потенциальная энергия системы равна
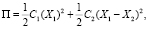
где C1 – жесткость пружин, на которых подвешен основной груз;
C2 – жесткость пружин, на которых подвешен дополнительный груз.
С учетом принятых допущений работа механической системы описывается системой дифференциальных уравнений Лагранжа второго рода, которые имеют вид:
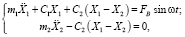(1)
где FB – возмущающая сила;
ω – частота колебаний внешних воздействий.
Вынуждающая сила FB может быть определена с учетом жесткости С0 пружины 15 и радиуса вращения R шарнира 13 (рис. 1):
FB = С0R.
Собственные частоты колебаний K1,2 механической системы можно определить из уравнения
,
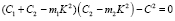или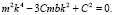 
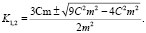
Частные решения уравнений (1) имеют вид
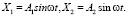
Амплитуды вынужденных колебаний массы 1 и массы 2 соответственно будут:
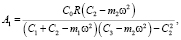
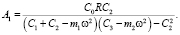
При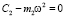 
амплитуда вынужденных колебаний массы m1 равна нулю.
Для данной установки параметры динамического поглотителя колебаний определяются из соотношения
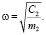
Фактическая сущность гашения колебаний состоит в том, что реакция присоединенной упругой связью груза в любой момент времени уравновешивает присоединенную к объекту возмущающую силу, а потом объект совершает лишь свободные колебания с частотой
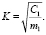
Частное решение уравнения (1) имеет вид
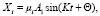
где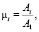 
Θ – фазовый угол.
Так как различные виды демпфирования можно заменить эквивалентным вязким демпфированием, то можно использовать линейное дифференциальное уравнение для гармонического движения.
Работа, совершаемая возмущающей силой Q•Cosωt в течение одного цикла, при установившемся поведении системы будет равна
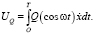(2)
Скорость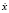 
можно определить по формуле
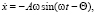(3)
где A – амплитуда вынужденных колебаний;
Подставив выражение (3) в (2), найдем
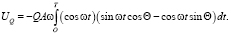(4)
В результате интегрирования выражения (4) получим
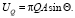
Аналогично определяем рассеиваемую за один цикл работу демпфирующей силы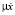 
, где μ – коэффициент вязкого сопротивления:
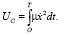(5)
Подставляя выражение (3) в (5), найдем
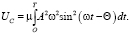(6)
Интегрируя выражение (6), определим величину энергии UC:
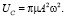
Таким образом, вносимая энергия UQ увеличивается в зависимости от амплитуды A по линейному закону, тогда как рассеиваемая энергия Uc возрастает пропорционально квадрату амплитуды. Они будут равны в точке пресечения кривых функций А0 для обоих видов энергии (рис. 3).
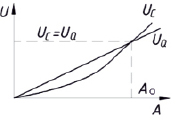
Рис. 3. Определение амплитуды колебаний при установившемся состоянии
Результаты экспериментальных исследований устройства поглощения колебаний показали его эффективность при работе механической системы в области резонансных частот. Настройка поглотителя колебаний сводилась к подбору массы груза m2 при заданной жёсткости пружины C2. В результате проведённых экспериментальных исследований получены осциллограммы переходных процессов в системе при различных режимах работы.
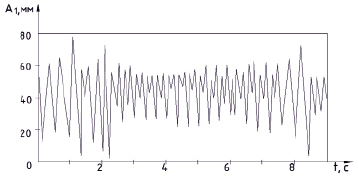
Рис. 4. Осциллограмма перемещений основной массы m1 без использования поглотителя колебаний
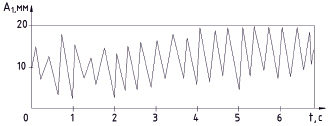
Рис. 5. Осциллограмма перемещений основной массы m1 с использованием динамического поглотителя колебаний
На рис. 4 представлена осциллограмма перемещений основной массы m1 без использования поглотителя колебаний. На рис. 5 представлена осциллограмма перемещений основной массы m1 с использованием динамического поглотителя колебаний при действии вынуждающей силы с частотой ω = 2,8с – 1.
Разность амплитуд колебаний массы m1 c применением динамического поглотителя инерционного типа по отношению к случаю, в котором он не применялся, составила ΔА1 = 29 мм. Применение динамического демпфирования позволяет снизить амплитуду колебаний на 81 % для данной модельной установки.
Заключение
1. Результаты экспериментальных исследований показали эффективность применения динамического поглотителя колебаний при работе механической системы в области резонансных частот.
2. Возможен выбор оптимальных параметров поглотителя колебаний с учётом минимизации динамических нагрузок в элементах машин.
3. Рассмотренное техническое решение позволяет снизить динамические нагрузки в узлах трансмиссии в зоне резонансных частот и повысить надёжность машин в целом.