Среди причин смертности населения России одно из первых мест занимает увеличение количества венозных тромбоэмболических осложнений в послеоперационный период. Например, при отсутствии адекватной профилактики, качественной ранней диагностики частота возникновения тромбозов глубоких вен у больных, которым выполняли эндопротезировании, достигает 60 % [1].
Существующие методы лабораторной диагностики тромбоэмболии (венография, реоплетизмография, дуплексное сканирование) имеют свои преимущества и недостатки и не дают чёткого представления о показаниях к их применению [2–4]. В настоящее время они не имеют достаточной интеллектуальной компьютерной поддержки принятия диагностических и-или терапевтических решений на основе обработки мультимодальной и нечеткой информации о состоянии пациента. Это обусловливает актуальность разработки теоретических основ, принципов построения и исследования соответствующих систем поддержки принятия диагностических решений прогноза тромбоэмболии (СППР ПТ), предназначенных для использования в клинических условиях и функционирующих с учетом специальным образом сформированного пространства информативных признаков [5, 6].
В настоящее время в клинической практике применяются следующие системы диагностики и терапии тромбоэмболизма (в том числе в процессе протезирования): система экспресс-диагностики тромбов и эмболий (М.А. Сидорова), технология дифференциальной диагностики тромбозов (Д. Николь), скрининг тромбоза глубоких вен (Clinical Preventive Strvices), автоматизированная система прогнозирования тромбоэмболических осложнений при травме [7, 8]. Современные медицинские системы поддержки принятия решений прежде всего основываются на достижениях в области искусственного интеллекта и системного анализа [9–11].
База знаний СППР ПТ или соответствующим образом специализированных экспертных систем представляет собой совокупность решающих классификационных правил, представленных в форме продукций, поскольку последние достаточно просто реализуются с помощью программных средств, хорошо интерпретируются и зарекомендовали себя при решении различных задач в медицинских экспертных системах [10]. Учитывая специфику медицинских данных, для синтеза баз знаний находят применение нейронные сети, структуры и параметры которых идентифицируются и оптимизируются с помощью самоорганизационных технологий, например генетические алгоритмы [12] или метод группового учета аргументов (МГУА). Использование в качестве признаков, характеризующих состояние пациента, логических переменных предполагает разработку адекватного математического аппарата.
Для синтеза антецедента (условия активации) решающих продукционных правил в случае представления характеризующих объект признаков в виде булевых переменных целесообразно использовать искусственные логические нейронные сети (ЛНС). Применяемый в настоящее время синтез ЛНС [13, 14] по сути, является итерационным процессом идентификации предикатов первого порядка, что не отвечает основным принципам самоорганизационного моделирования.
Между тем сетевые принципы синтеза моделей, лежащие в основе метода группового учета аргументов (МГУА), доказали свою перспективность в аналогичных случаях при анализе сложных открытых систем в медицинской предметной области [15].
В связи с этим аналогично МГУА предлагается использовать нейроны логической сети с ограниченным и небольшим количеством входов, постепенно усложняя структуру логической функции, «продвигаясь внутрь» по рядам ЛНС.
Ограничение на количество входных аргументов одного нейрона приближено к естественному интеллекту, который «одновременно удерживает» в оперативной обработке ограниченное количество информации об объектах, процессах или семантических группах (включая альтернативные решения). Минимальным в этом случае является искусственный логический нейрон с двумя входами и одним выходом – бинарный нейрон – структура представлена на рис. 1.
На рисунке обозначено: Fb(a, b) – логическая функция двух логических переменных; y – логическая переменная y = Fb(a, b); Fa(y) – функция активации; OUT – выходной сигнал нейрона, представляющий собой строковую переменную для логической функции Fb(a, b), выполнение которой идентифицирует принадлежность объекта распознавания нейроном к определенному классу – для двух переменных; yac – сигнал функции активации, используемый для работы в сети: в данном случае: yac = Fb(a,b); Pout – модуль формирующий строку OUT по Fb(a, b) и идентификаторам <признаков> х и у, используемых в качестве «входов» нейрона a и b соответственно.
Переменная OUT записывается в виде аналога польской инверсной записи для логических функций: OUT = «(x)(y)φρπ» (x – идентификатор <признака> для переменной a, y – идентификатор <признака> для переменной b, φ – идентификатор логической функции между переменными х и у, ρ и π – идентификаторы логических функций true или false над переменными a и b , обозначенными символами «1» и «0», соответственно.
Обучение нейрона заключается в выборе функции Fb(a, b) из всего множества доступных логических функций таким образом, чтобы нейрон при заданной функции активации обеспечивал минимальную ошибку распознавания образа в обучающей выборке.
Базовая структура интерактивной логической нейронной сети на основе идеологии МГУА (ЛНС МГУА) представлена на рис. 2.
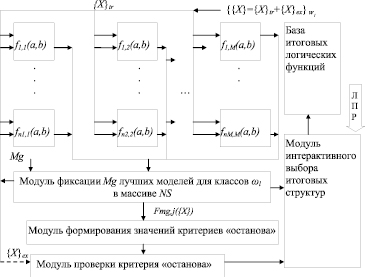
Рис. 2. Базовая структура интерактивной логической нейронной сети ЛНС МГУА на основе бинарного нейрона
На схеме, изображенной на рис. 2, используются следующие обозначения: – ЛПР – лицо принимающее решение; – {{X} = {X}tr + {X}ex}ωl – выборка значений признаков (представленных в логической шкале измерений), зарегистрированных для N объектов исследования (пациентов), принадлежащих к эмпирически (клинически) подтвержденному классу (состоянию, заболеванию, прогнозу) ωl и методом рандомизации разделенная на две подвыборки {X}tr – обучающая и {X}ex – экзаменационная (значения признаков объекта z расположены в строках с индексом z выборок-матриц, в строках с индексом «0» – идентификаторы признаков); fi,j(a, b) – i-ый бинарный нейрон типа NL или NLA соответствующий j-мо ряду сети, входными сигналами (синапсами) которого являются логические переменные a и b, выходными: значение итоговой логической функции нейрона OUTi,j; Mg – величина характеризующая свободу выбора принятия решения в терминологии самоорганизационного моделирования – в данном случае, количеству функций Fmg,j({X}) (mg = 1,…,Mg). (Mg>1, по аналогии с опытом применения МГУА рекомендуется принимать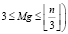 
; Fmg,j({X}) – логическая функция и ее аргументы, определяемая строковой переменной OUT; NS – массив, в котором фиксируются лучшие варианты настройки нейронной сети. Массив состоит из трех столбцов: первый – номер ряда (используется для внутренней работы нейронной сети в процессе настройки), второй столбец – лучшие в смысле выбранного критерия селекции строковые переменные OUT – используются как для селекции лучших логических функций, так и для функционирования ЛНС МГУА на этапе распознавания или формирования итоговой логической функции (в ячейках третьего столбца находятся значения критерия селекции Ks).
Если считать рассмотренную структуру, представленную на рис. 2, аналогом МГУА-структуры идентификации полинома Колмогорова – Габора, то можно ожидать, что при правильном формировании множества {X}, последующего его упорядочивания по степени информативности входящих признаков и введения ограничений на порядок перебора аргументов нейронной сети (особенно на первом ряду) – в первую очередь рассматривать пары наиболее информативных показателей, – то общее количество рядов сети следует ожидать меньше величины n/5 (n – количество признаков).
В качестве апробации возможностей ЛНС МГУА для синтеза условий активации использовалась задача синтеза адекватного решающего правила прогноза развития тромбоэмболии легочной артерии (ТЭЛА) в послеоперационный период протезирования крупных суставов.
В ходе вычислительного эксперимента получен антецедент продукционного правила:
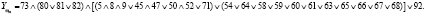
В формуле числами обозначен признак, соответствующий наблюдению у пациента следующего фактора риска: 5 – ожирение, 8 – дегидратация или полицетемия, 9 – недостаточность кровенаполнения, 45 – острая дыхательная недостаточность, 47 – потеря сознания, 50 – анемия, 52 – перфузия левого желудочка на ЭКГ, 54 – локализация тромба (вены стопы), 58 – локализация тромба (малая берцовая вена), 59 – локализация тромба (коммуникантные вены), 60 – локализация тромба (глубокие вены бедра), 61 – локализация тромба (наружная подвздошная вена), 63 – локализация тромба (общая подвздошная вена), 64 – локализация тромба (вены таза), 65 – локализация тромба (подключичная вена), 66 – локализация тромба (вены верхней конечности), 67 – локализация тромба (источник не выявлен), 68 – локализация тромба (подколенная артерия), 71 – локализация тромба (НПВ), 73 – флотирующий тромб, 80 – пробы Мозеса, 81 – пробы Хоманса, 82 – пробы Левенберга, 83 – рентген (как проба), 92 – нарушение венозной гемодинамики (средневыраженный отек).
ЕСЛИ у пациента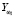 
= true, ТО его состояние соответствует возможному развитию послеоперационной ТЭЛА с уверенностью 0,92.
(Значение уверенности получено в ходе клинических испытаний решающего правила на репрезентативной экзаменационной выборке, состоящей из 829 человек с клинически подтвержденными диагнозами: 327 – наблюдалась ТЭЛА в послеоперационный период, 502 – не наблюдалась).
Поскольку на значение риска прогноза возникновения и развития ТЭЛА существенно влияет возрастной фактор, то значение коэффициента уверенности предлагается умножать на возрастной коэффициент Кage, который предлагается вычислять по формуле
где age – возраст в годах.
График поведения функции Кage представлен на рис. 3.
Полученные результаты позволяют предположить эффективность предлагаемого подхода синтеза решающих правил продукционного типа для баз знаний медицинских экспертных систем, как системообразующего модуля автоматизированных систем поддержки принятия решений в хирургии, поддерживающих оптимальную терапию и-или профилактику заболеваний, возникающих в послеоперационный период и приводящих впоследствии с высокой степенью риска к инвалидности или летальности. Это обусловливается тем, что предлагаемый подход ЛНС МГУА основан на синергетическом подходе к обработке гетерогенной структуры данных, представленных логическими значениями, позволяющих существенно уменьшить субъективизм при регистрации признаков – факторов риска.