Одним из наиболее тяжелых в управлении и наиболее накладным в плане расходов этапом производства любой зерновой культуры является период уборочных работ. Для проведения уборки урожая в рациональные сроки и в значительно эффективном режиме сельскохозяйственные компании используют большое количество технических средств, комплексное управление которыми является довольно трудной задачей. И это, естественно, связано с тем, что в процессе принятия действенных решений нужно рассматривать значимый объём данных о свойствах и характеристиках инженерно-технических ресурсов, которые были привлечены в уборочно-транспортных работах, и среде их эксплуатации. Для решения этих сложностей используюб экономико-математические алгоритмы, алгоритмы теории массового обслуживания, логистического и имитационного моделирования [1]. Но такие подходы не позволяют в полной мере учитывать такие особенности инженерно- технологического процесса уборочных работ, как стохастичность и нестационарность поведения, невоспроизводимость экспериментальных результатов, недостаточную информативность о характеристиках процесса. Эти особенности инженерно-технологического процесса необходимо учесть в дальнейшем при решении задач оперативного управления и планирования сельскохозяйственных работ за счёт использования методов нечёткой логики (НЛ) и теории нечётких множеств (НМ).
На этапе планирования работ перед уборкой урожая наиболее актуальной является задача прогноза расхода топлива для комбайнов. Значимость проблемы обусловлена тем, что нормы расхода топлива определяются для идеальных машин без учёта условий эксплуатации и изменения ресурса автомобиля, вследствие чего параметры прогнозируемых затрат могут отличаться от фактических в достаточно широком диапазоне.
К факторам, которые наиболее влияют на затраты топлива, можно отнести следующие: урожайность культуры, эксплуатационный ресурс комбайна и длина так называемого гона поля [2]. В реальных условиях при расчете достоверного поправочного коэффициента к идеальной норме затрат по данным параметрам будет присутствовать некая неопределенность, которая в общем-то требует применения алгоритмов нечеткой логики.
Постановка задачи
Постановка задачи: разработать методику прогноза значения реального поправочного коэффициента к норме расхода топлива (ПКРТ) на основе методов НЛ, которая позволит при прогнозировании учитывать влияние технологических условий эксплуатации техники, а также оптимальных сроков ее эксплуатации на основной показатель – общий расход топлива.
Надо учитывать, что данные, необходимые для строительства базы нечётких правил, являются количественными, а не лингвистическими и базу нечётких правил (БНП) сформируем с использованием универсального метода построения на основе численных данных [3; 4]. Главный принцип НЛ – это замена параметров истина и ложь на степень истинности. Для определения эксплуатационной скорости зерноуборочного комбайна предложено использовать методы теории искусственных нейронных сетей, которые, в отличие от других методов прогнозирования, позволяют получать более адекватные реальности решения. Это связано с тем, что искусственная нейронная сеть может совершенствовать точность своего прогноза по мере накопления ею опыта.
Решение задачи
Нечеткая логика имеет общепринятые алгоритмы представления знаний на базе правил для лингвистических переменных, но они требуют затрат по времени и ресурсам для инициализации функций конструирования и принадлежности. Нейросетевой алгоритм обучения автоматизирует этот процесс и существенно сокращает затраты и время на создание и разработку, при этом оптимизируя параметры искомой системы.
Системы, которые используют нейронные сети для инициализации параметров таких нечетких моделей, называют нейронной нечеткой системой. Для решения этой задачи был выбран трехслойный персептрон, который обучался методом обратного распространения ошибки. В частности, первый слой сети содержит сорок нейронов, второй – двадцать, а третий – один нейрон. В качестве функции активации в первых двух слоях выбран гиперболический тангенс и линейная функция в третьем слое. Структура искусственной нейронной сети приведена на рис. 1.
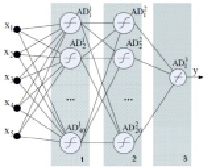
Рис. 1. Структура искусственной нейронной сети прогноза скорости комбайна
Стандартная структура системы, которая использует нечеткую логику, включает в себя базу знаний, фаззификацию, блок решений, дефаззификацию.
Рассмотрим вначале основные этапы построения базы нечётких правил.
1. Разделение пространств выходных и входных данных на области. На основе статистических данных, взятых из источника [2], сформируем множество обучающих данных (ОД), которые состоят из векторов (ОВ):
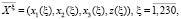 (1)
(1)
где ξ – номер во множестве ОД; x1(ξ) – общая урожайность культуры, ц/га; x2(ξ) – размер гона поля, м; x3(ξ) – срок эксплуатации зернового комбайна, лет; z(ξ) – искомое значение поправочного коэффициента к расчетной затрате топлива.
Кроме того, определим фиксированные максимальные и минимальные значения выходных и входных переменных: x1(ξ)∈[10, 100], x2(ξ)∈[100, 200], x3(ξ)∈[0, 50], z(ξ)∈[0, 95, 4]. Каждую из этих областей определения разделяем на три отрезка, задаем функции принадлежности НП, характеризующих входящие/ выходящие переменные [5].
2. Синтез нечётких правил (НП) на основе ОД. Для формирования НП необходимо определить граничные характеристики принадлежности каждого компонента ОВ к определенным отрезкам. Нечёткие правила в общем виде [8]:
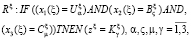 (2)
(2)
где ξ – НП, Uα – НМ урожайность культуры, Bς – НМ для гона поля, Cμ – НМ для срока эксплуатации комбайна, Kγ – НМ для коэффициента поправки к расчетным нормам затрат топлива для комбайнов.
3. Распределение степени истинности для каждого НП. На этом этапе решаются задачи противоречивых правил, преимущественно имеющие одинаковые условия при различных заключениях. По определению НЛ при установке правил задаётся некая степень истинности (в противоположность булевым значениям) с последующим отбором того правила, в котором степень истинности будет максимальная. Для правила Rξ величина истинности SR находится по формуле
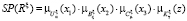 , (3)
, (3)
где 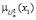 ,
, 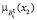 ,
, 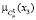 – значение функции принадлежности параметра x1(ξ), x2(ξ) и x3(ξ) к соответствующему НМ,
– значение функции принадлежности параметра x1(ξ), x2(ξ) и x3(ξ) к соответствующему НМ,
Cμ, – значение функции принадлежности параметра z(ξ) к множеству Kγ.
4. Создание базы нечётких правил. БНП представим в виде 3D матрицы, cо значениями нечётких множеств K1, K2, K3. Измерения матрицы x1, x2, x3 и на оси x1 заданы НМ U1, U2, U3. В БНП внесём 27 правил.
Имея БНП, легко определить количественное значение для выходной переменной 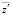 при входящих сигналах
при входящих сигналах 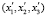 .
.
Расчёт выходной переменной осуществляется с нечеткими входами на базе алгоритма дефаззификации по среднему центру:
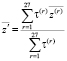 , (4)
, (4)
где τ(r) – степень активности r правила, которая находится по правилу
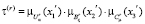 . (5)
. (5)
Данный метод можно распространить и на случаи с произвольным числом входов/выходов нечеткой системы. Ниже показан алгоритм построения базы правил для программной реализации.
1. Распределить пространство значение x1(ξ)∈[10, 50], x2(ξ)∈[100, 1500], x3(ξ)∈[0, 25], z(ξ)∈[0, 95, 2], для каждого создать соответствующие функции принадлежности;
2. Создать и инициализировать таблицу Т[U, B, C] степеней истинности правил;
3. Выбрать пару данных для x1(ξ)∈[10, 50], x2(ξ)∈[100, 1500], x3(ξ)∈[0, 25], z(ξ)∈[0, 95, 2].
4. Установить степень принадлежности данных к областям (нечетким множествам) и оформить соответствующее правило
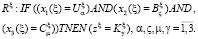
5. Установить степень истинности правила R по формуле
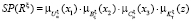 ,
,
если SP(R) > T, то вписать правило R в таблицу BR и Т: BR[U, B, С] = K и T[U, B, С] = SP(R), иначе п. 4.
6. Конец цикла, то п .7, иначе п. 4.
7. Конец программы.
На основе данных об эксплуатационной скорости и расхода топлива для зерноуборочных комбайнов можно определить такие характеристики технологического процесса уборочной кампании, как интенсивность уборки зерна комбайнами и эксплуатационные затраты [6]. Эти характеристики вместе с показателями аренды комбайнов, урожайности полей, размера полей, стоимости зерна являются исходными данными задачи распределения уборочной техники по полям.
Приведение к нечеткости. Во входном потоке находится база правил Rξ и массив данных А = {a1,…, ax}. Для всех подусловий в базе правил ставится в соответствие матрица истинности.
Программа выполнена в коде с#. В качестве входных данных используется база правил (List<Prav>).
Таблица истинности строится на b[i], соответствующих входным a[i]. В отличие от «математической» истинности в нечеткой логике значения b[i] формируют массив вероятностей [0..1] наступления события [7].
Дефаззификация в результате дает количественное значение для выходных лингвистических переменных. В данной реализации алгоритма используется метод по среднему центру, в котором значение i-ой переменной вычисляется по формуле (4).
private double[] defaz(List<FuzBD> FuzBD) {
double[] y = new double[x];// x = 27 – кол-во вх. параметров
for(int i1 = 0; i1 < s; i1++) // s – кол-во вых. параметров
{ double fuzA = integral(FuzBD.get(i1), true);
double fuzB = integral(FuzBD.get(i1), false);
y[i1] = fuzA / fuzB;
}
return z;
}
Для построения самих нейронных сетей был использован алгоритм Random Forest, для разработки и обучения нейронные сети. В результате моделирования были созданы нейронная сеть с трехслойным персептроном. Оценка прогнозирования результатов расхода топлива основывалась на подборе истинных прогнозированных значений доверительного интервала, и в процессе моделирования отсекались, подчитывались все граничные спрогнозированные значения вне доверительного интервала. Оставшиеся результаты удовлетворяли необходимому критерию качества прогноза (рис. 2).
Траектории выходных данных в сравнении с экспоненциальной моделью из стандартных нормативов. На рис. 2 изображены определенные точки моделированного профиля урожайности и срока эксплуатации, где красная кривая обеспечивает экспоненциальное описание профиля поправочного коэффициента расхода топлива по нормативам.
Если урожайность 30÷35 ц/га, то норма расхода для 33 ц/га составит 12,7 га. Если рассчитать норму на 35 ц/га, то (12,7×33,0):35 = 12,0 га, а норма расхода топлива (10,5×12,7):12 = 11,1 л на гектар. Учитывая коэффициент, программа определяет поправочный коэффициент 11,1×1,109 = 12,31 л/га (рис. 3).
Данные переводятся в нечеткий формат согласно определенным функциям принадлежности, внутри класса расчета происходит их обработка, полученные при этом изменения значения поправочного коэффициента дефаззифицируются и результат решения поступает в виде сигнала и графика на монитор.
Выводы
Результаты были приближены к линейной зависимости реального и спрогнозированного значений: Xпрогноз = Xреальное + δ. Все полученные результаты укладываются в доверительный интервал, что позволяет говорить о достаточно высокой точности нейронной нечеткой системы для прогноза поправочного коэффициента.
Применение разработанного алгоритма нечеткой оценки для поправочного коэффициента к идеальной норме затраты топлива представляет высокую вероятность получить адекватный результат для комбайнов с неравномерным эксплуатационным ресурсом в зависимости от значимых характеристик полей. В дальнейших исследованиях необходимо использовать контроллеры управления расхода топлива в зависимости от ПКРТ.
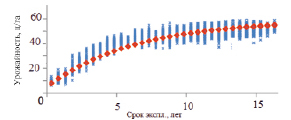
Рис. 2. ПКРТ на базе двух входных значений
Статистический результат моделирования некоторых схем
|
Входные данные |
Выходные данные |
|||
|
Схема |
Урожайность культуры, ц/га |
Размер гона поля, га |
Срок эксплуатации, лет |
Поправочный коэф. z |
|
Э1 |
60 |
50 |
0 |
1,001 |
|
Э2 |
30 |
400 |
20 |
1,101 |
|
Э3 |
50 |
400 |
10 |
1,049 |
|
Э4 |
60 |
800 |
10 |
1,142 |
Примечание. Схема Э1: низкая урожайность, отсутствие эксплуатационного износа комбайна (ЭИК), малый гон поля. Схема Э2: средний урожай, высокий ЭИК, средний гон поля. Схема Э3: средняя урожайность, средний износ комбайна ЭИК, средний гон поля. Схема Э4: высокая урожайность, средний ЭИК, большой гон поля.
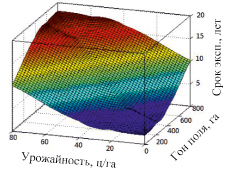
Рис. 3. 3D график значения поправочного коэффициента
Решение задач прогноза оценивания коэффициента к норме расхода топлива для уборочной техники ИИ позволяет получить эффективные решения с учетом особенностей данной предметной области. Рассмотрены модели и алгоритмы, как знания, включенные в состав базы знаний гибридной интеллектуальной системы управления уборочной кампанией, которая предназначена для поддержки принятия решений по управлению уборочно-транспортными работами в условиях современного сельскохозяйственного предприятия.



