Рассматриваемая система представляет собой объект, излучающий переменное электромагнитное поле, образованное приложенным к нему напряжением в нормальной среде, и объект, на который воздействует переменное электромагнитное поле, т.е. чувствительный элемент, расположенный на некотором расстоянии от излучающего объекта, реагирующий только на электрическую составляющую электромагнитного поля и преобразующий её для дальнейшего использования [4, 5, 10].
Задача определения наличия электрического напряжения, а также в дальнейшем и определения его уровня на излучающем электромагнитное поле объекте, является сложной задачей. Сложность формы переменного электромагнитного поля, его распространение в нормальной среде и преобразование для дальнейшего получения информации невозможно без предварительных исследований на математической модели, которая в достаточной мере и с необходимой точностью отображает его свойства и вид.
Для упрощения сложных объектов и понимания происходящих процессов в системах, используют математическое моделирование. Также необходимо создание схожей с оригиналом модели.
Методом моделирования называется замена объекта – оригинала объектом-заместителем, обладающим определенным сходством с оригиналом, с целью получения новой информации об оригинале. Моделью называется объект-заместитель объекта-оригинала, предназначенный для получения информации об оригинале.
Моделирование применяется в тех случаях, когда проведение реального эксперимента сопряжено с опасностью, высокими экономическими и временными затратами или эксперимент неудобен в масштабе пространства и времени.
Цель работы: анализ существующих методов математического моделирования и выбор наиболее оптимального.
Материал и методы исследования: методы математического моделирования, теории планирования эксперимента, теории измерений.
Результаты исследования и их обсуждение
Методами математического моделирования решается широкий круг задач теории электромагнитных полей. Преимущества методов математического моделирования наиболее ярко проявляются при решении задач распространения электромагнитных полей и их преобразования. Критериями для преобразования электромагнитного поля могут служить габариты преобразователя, материал из которого он изготовлен, расстояние, на котором находится преобразователь от объекта излучения, его экранирование и т.п. При оптимизации конструкции преобразователя важно выделить параметры, которые существенно влияют на его чувствительность:
– расположение преобразователя в пространстве;
– количество источников электромагнитного излучения, расположенных в непосредственной близости к преобразователю;
– форма электромагнитного поля;
– интенсивность электромагнитного поля;
– форма излучателя электромагнитного поля;
– влияние окружающей среды.
Для успешного решения указанных задач требуется разработка численных методов, их качественная реализация в виде программных средств, обеспечение диалогового общения пользователя с ЭВМ, так как аналитические методы имеют жесткие ограничения по области применения и используются обычно для геометрически простых систем или частей сложной системы, как правило, в линейной постановке. Такая технология исследований с широким применением цифровых моделей и ЭВМ получила название вычислительного эксперимента [1].
Вычислительный эксперимент отличается от натурального объемом и качеством информации. В вычислительном эксперименте объем получаемой информации не ограничивается числом источников излучения, количеством датчиков и их быстродействием. Оказываются возможными вычислительные эксперименты в очень широком диапазоне конструктивных параметров и режимов работы устройств, включая внештатные ситуации. Изменение физических свойств материалов и геометрических размеров позволяет просмотреть все возможные варианты распространения электромагнитного поля, его формы и неоднородности, а также все возможные варианты преобразователей электромагнитного поля. Важной особенностью вычислительного эксперимента является повторяемость результатов, отсутствие случайной ошибки, связанной с действием неучтенных факторов.
Для составления целостной картины распределения и преобразования электромагнитного поля, а также разработки преобразователя требуется предварительный расчет электромагнитной задачи. При этом необходимо учитывать возможность нагрева чувствительного элемента под действием электромагнитных полей.
В первую очередь основным критерием выбора метода математического моделирования является решение задач расчета и построения сложных электромагнитных полей.
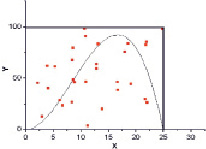
Рис. 1. Численное интегрирование функции методом Монте-Карло
Одним из методов математического моделирования является метод статистических испытаний [2]. К такому методу относится геометрический алгоритм Монте-Карло интегрирования. Для определения площади под графиком функции можно использовать следующий стохастический алгоритм (рис. 1):
– ограничим функцию прямоугольником (n-мерным параллелепипедом в случае многих измерений), площадь которого Spar можно легко вычислить; любая сторона прямоугольника содержит хотя бы одну точку графика функции, но не пересекает его;
– поместим в этот прямоугольник некоторое количество точек N, координаты которых будем выбирать случайным образом;
– определим число точек K, которые попадут под график функции;
– площадь области, ограниченной функцией и осями координат, S = Spar(K/N).
Для малого числа измерений интегрируемой функции производительность Монте-Карло интегрирования гораздо ниже, чем производительность детерминированных методов. Тем не менее в некоторых случаях, когда функция задана неявно, а необходимо определить область, заданную в виде сложных неравенств, стохастический метод может оказаться более предпочтительным. При том же количестве случайных точек точность вычислений можно увеличить, приблизив область, ограничивающую искомую функцию, к самой функции. Для этого необходимо использовать случайные величины с распределением, форма которого максимально близка к форме интегрируемой функции. На этом основан один из методов улучшения сходимости в вычислениях методом Монте-Карло. Недостатком метода статистических испытаний является очень большой объем моделирования.
С развитием математического моделирования были предложены интерполяционный метод и метод Б.Г. Доступова для систем невысокой сложности. Одним из способов представления интерполяционного полинома n-степени является многочлен в форме Лагранжа. Данный полином представляет собой математическую функцию, позволяющую записать полином n-степени, который будет соединять все заданные точки из набора значений, полученных опытным путем или методом случайной выборки в различные моменты времени с непостоянным временным шагом измерений. В общем виде интерполяционный многочлен в форме Лагранжа записывается в следующем виде [6]:
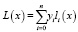 ,
,
где n – степень полинома L(x); li(x) – базисные полиномы (множитель Лагранжа), которые определяются по формуле
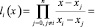
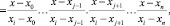
где x0, x1… xi -1, xi+1… xn, xj – корни многочлена; yi – константа.
Базисные полиномы li(x) обладают следующими свойствами: являются многочленами степени n; li(xi) = 1; и li(xi) = 0 при j ≠ i.
Недостаток интерполяционного метода – большой объем данных для моделирования. Этот недостаток – следствие того, что метод не полностью использует все априорные сведения о динамике функционирования системы и не учитывает особенностей законов распределения параметров системы. Более полно указанные свойства учитывает метод Б.Г. Доступова, применяемый при анализе точности нелинейных автоматических систем сравнительно невысокой сложности. Этим методом удается достичь такого положения, при котором необходимое число интегрирований исходной системы уравнений линейно зависит от числа параметров, определяющих закон распределения входных случайных параметров и случайных начальных условий. Для сложных систем, когда они описываются сложными математическими конструкциями, преимущества метода резко снижаются. В силу того, что метод статистических испытаний более прост в программном исполнении, область применения метода Доступова, так же как и интерполяционного, является менее обширной.
К другим методам математического моделирования для построения и расчета сложных систем относятся: метод конечных элементов, метод конечных разностей и метод граничных элементов [3]. Широкое использование и развитие численных методов началось с методов конечных разностей (МКР) [9]. Эти методы основаны на замене дифференциальных операторов в уравнениях математической физики конечно-разностными операторами в соответствии с построенной сеткой (пространственная дискретизация области и ее границ заключается в построении сетки, состоящей из узлов и ребер). Путем такой замены дифференциальные уравнения в частных производных преобразуются в систему алгебраических уравнений относительно узловых величин. В случае однородной среды переход к разностным уравнениям осуществляется путем простого применения конечно-разностных операторов. Для уточнения аппроксимации частных производных в состав этих операторов могут включаться конечные разности высших порядков. В случае кусочно-неоднородной среды к узлам, принадлежащим поверхностям раздела сред, вместо обычных разностных операторов применяются условия сопряжения, отражающие скачкообразные изменения частных производных. Аппроксимация частных производных по обе стороны от границы раздела сред выражается также через конечные разности. Граничные условия Дирихле учитываются простым заданием искомых величин в граничных узлах. Граничные условия Неймана или Коши аппроксимируются с помощью конечно-разностных операторов. Главным недостатком МКР является сложность в анализе непрямолинейных границ.
Основным свойством получаемых систем конечно-разностных уравнений является ленточная или профильная структура матрицы коэффициентов. Ширина ленты или профиля определяется нумерацией узлов, регулярностью сетки, максимальным порядком конечных разностей, используемых для аппроксимации частных производных. Как правило, матрица коэффициентов характеризуется слабой заполненностью внутри ленты или профиля даже при оптимальной нумерации узлов, поэтому для ее хранения в памяти ЭВМ часто применяется технология разреженных матриц. Методы решения систем сеточных уравнений определяются их свойствами. Методы матричной прогонки являются основой для решения систем сеточных уравнений и основываются на гауссовом исключении или факторизации применительно к ленточным матрицам. Другие прямые методы основаны на различных видах разложения на множители применительно к разреженным матрицам. Основным недостатком прямых методов является плохая приспособленность их к компактным схемам хранения разреженным матриц (при факторизации происходит их заполнение). Поэтому приходится использовать итерационные методы, основанные на нахождении по приближенному значению величины следующего приближения. Метод позволяет получить значения корней системы с заданной точностью в виде предела последовательности некоторых векторов.
Помимо конечно-разностных методов решения задач математической физики существуют методы, обладающие свойствами как численных, так и аналитических: методы интегральных уравнений, вариационные и проекционные методы (методы взвешенных невязок и связанные с ними методы конечных (МКЭ) и граничных элементов) [8].
Метод конечных элементов основан на интегральной формулировке граничной задачи. Вместо дифференциальных уравнений с частными производными устанавливаются соответствующие функционалы. Исследуемая область в зависимости от размерности задачи делится на плоские или объемные элементы, в которых неизвестное распределение поля аппроксимируется полиномами. Использование метода Рэлея – Ритца позволяет затем получить систему линейных алгебраических уравнений. Поскольку некоторые из выделенных элементов включают границы исследуемой области, полученная система уравнений может быть решена для внутренних точек. МКЭ имеет некоторое преимущество перед методом конечных разностей в гибкости, так как с его помощью легко учитываются сложные границы. Порядок аппроксимирующих полиномов дает дополнительную свободу при численном расчете. Недостаток метода – требуются большие объемы памяти ЭВМ и высокая вычислительная мощность. Пример реализации данного метода представлен на рис. 2. В пакете ANSYS Maxwell [12] проведено разбиение исследуемой области на конечные элементы, в данном случае – треугольники, моделью для исследования является пропорциональный электромагнит постоянного тока [12].
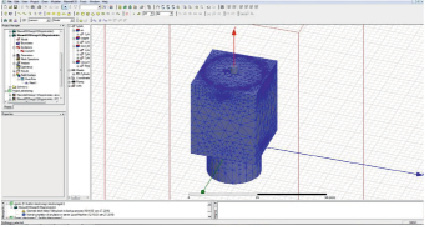
Рис. 2. Применение метода конечных элементов для исследования электромагнита
Метод граничных элементов [7], сочетая достоинства аналитических и численных методов, позволяет легко описать объект любой формы, обладает высокой устойчивостью за счет малой ширины ленты матрицы жесткости, более точно описывает распределение электромагнитного поля при небольшом числе элементов по сравнению с методом конечных разностей Данный метод обладает следующими недостатками: рассматриваются граничные условия одного типа – либо Дирихле либо Неймана, смешанная задача не рассматривается (не составляет труда записать уравнения смешанной задачи, но они не имеют теории решения); граница должна быть гладкой (полученные при решении задачи Неймана сингулярные интегралы не существуют в угловых точках кусочно-гладкой границы); матрица результирующей системы линейных алгебраических уравнений – полностью заполненная, в отличие от МКЭ, в котором она содержит большое количество нулей.
Заключение
Исходя из проведенного анализа методов математического моделирования, наиболее оптимальным является МКЭ, так как он позволяет описывать сложную геометрию исследуемых объектов и учитывает существующие нелинейности при анализе полевых задач. Кроме того, данный метод обладает универсальностью формы построения вычислительных алгоритмов.
Результаты работы получены при поддержке гранта РФФИ № 16-38-50278 «Исследование и разработка принципов построения бесконтактного измерителя переменного скалярного потенциала электрического поля, действующего в условиях неоднородного электромагнитного поля». Работы были выполнены с использованием оборудования ЦКП «Диагностика и энергоэффективное электрооборудование» ЮРГПУ(НПИ).



